第24章 圆-专题训练：与圆的切线有关的计算与证明 人教版数学九年级上册作业课件

这是一份第24章 圆-专题训练：与圆的切线有关的计算与证明 人教版数学九年级上册作业课件，共13页。

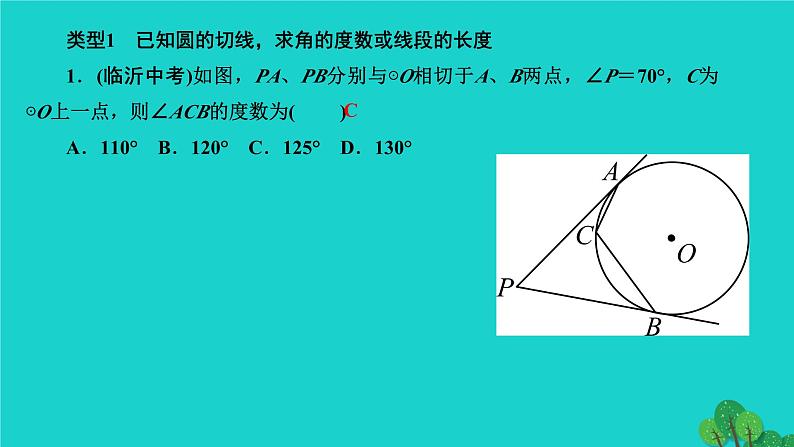
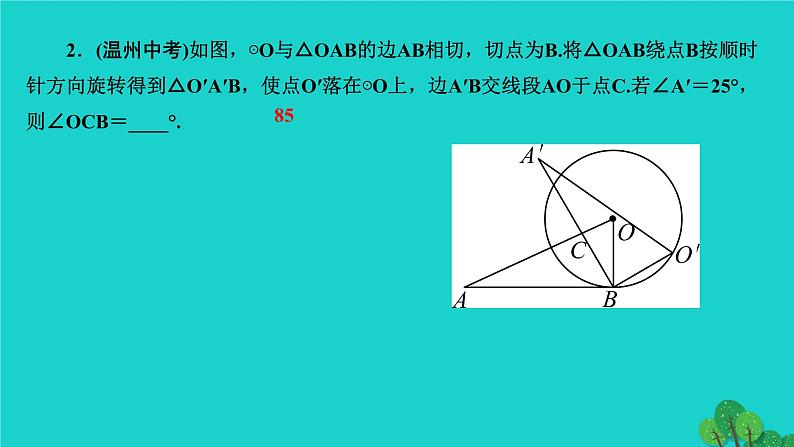
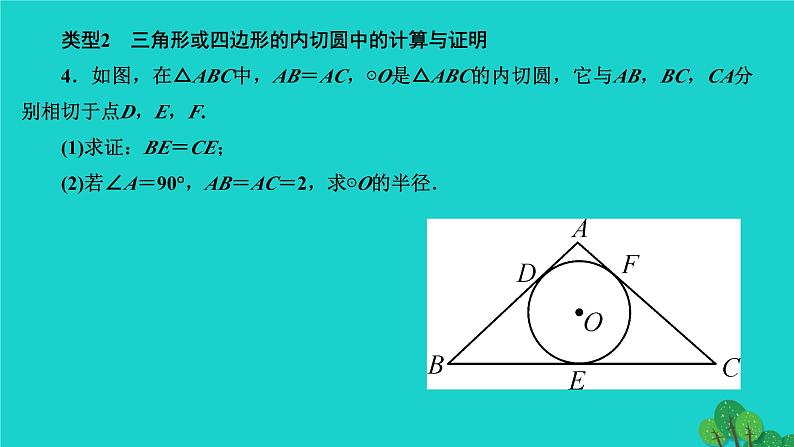
专题训练(十六)　与圆的切线有关的计算与证明第二十四章　圆类型1　已知圆的切线，求角的度数或线段的长度1．(临沂中考)如图，PA、PB分别与⊙O相切于A、B两点，∠P＝70°，C为⊙O上一点，则∠ACB的度数为( )A．110° B．120° C．125° D．130°C2．(温州中考)如图，⊙O与△OAB的边AB相切，切点为B.将△OAB绕点B按顺时针方向旋转得到△O′A′B，使点O′落在⊙O上，边A′B交线段AO于点C.若∠A′＝25°，则∠OCB＝____°.853．(凉山州改)如图，等边三角形ABC的边长为4，⊙C的半径为，P为AB边上一动点，过点P作⊙C的切线PQ，切点为Q，求PQ的最小值．类型2　三角形或四边形的内切圆中的计算与证明4．如图，在△ABC中，AB＝AC，⊙O是△ABC的内切圆，它与AB，BC，CA分别相切于点D，E，F.(1)求证：BE＝CE；(2)若∠A＝90°，AB＝AC＝2，求⊙O的半径．5．如图，四边形ABCD外切于⊙O，切点分别是E、F、G、H.(1)请探索四边形ABCD四边AB、BC、CD、AD之间的关系；(2)圆的外切平行四边形是____形；圆的外切矩形是______形；(3)若AB∶BC∶CD∶DA＝1∶3∶4∶x，且四边形ABCD的周长为20 cm，求x及AD的长．菱正方解：(1)∵四边形ABCD外切于⊙O，切点分别是E、F、G、H，∴AH＝AE，BE＝BF，CF＝CG，DG＝DH，∴AH＋DH＋CF＋BF＝DG＋CG＋AE＋BE，即AD＋BC＝AB＋CD(3)∵AB∶BC∶CD∶DA＝1∶3∶4∶x，AD＋BC＝AB＋DC，∴1＋4＝3＋x，则x＝2，∵四边形ABCD的周长为20 cm，∴20÷(1＋3＋4＋2)＝2，∴AD＝2×2＝4(cm).