2024届人教A版高考数学一轮复习高考中立体几何解答题的提分策略课件2

这是一份2024届人教A版高考数学一轮复习高考中立体几何解答题的提分策略课件2，共17页。PPT课件主要包含了思维导引1，感悟升华等内容，欢迎下载使用。
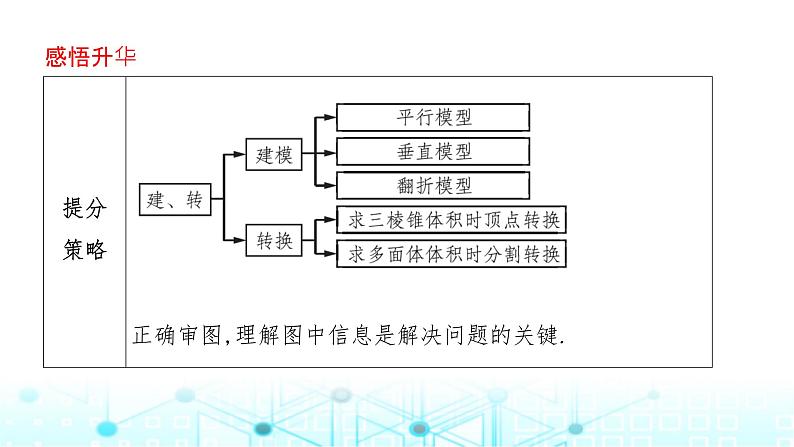
考情解读 每年高考数学试卷都有一道立体几何解答题.主要采用“论证与计算”相结合的模式,即先利用定义、定理、公理等证明空间的线线、线面、面面平行或垂直,再利用有关公式计算空间几何体的体积.解决立体几何问题常用的数学思想方法为转化与化归(空间问题转化为平面问题).
1.典例 [2021全国卷甲,12分][文]如图,已知直三棱柱ABC-A1B1C1中,侧面AA1B1B为正方形,AB=BC=2,E,F分别为AC和CC1的中点,BF⊥A1B1.(1)求三棱锥F-EBC的体积;(2)已知D为棱A1B1上的点,证明:BF⊥DE.
规范答题 (1)由题设可知,PA=PB=PC, (2分)由于△ABC是正三角形,故可得△PAC≌△PAB,△PAC≌△PBC.(3分)又∠APC=90°,故∠APB=90°,∠BPC=90°.(4分)从而PB⊥PA,PB⊥PC,又PA∩PC=P,故PB⊥平面PAC.因为PB⊂平面PAB,所以平面PAB⊥平面PAC.(6分)
3.典例 [2019全国卷Ⅰ,12分][文]如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.(1)证明:MN∥平面C1DE.(2)求点C到平面C1DE的距离.