



所属成套资源:全套2024届人教A版高考数学一轮复习教学课件
2024届人教A版高考数学一轮复习空间空间点直线平面之间的位置关系课件1
展开
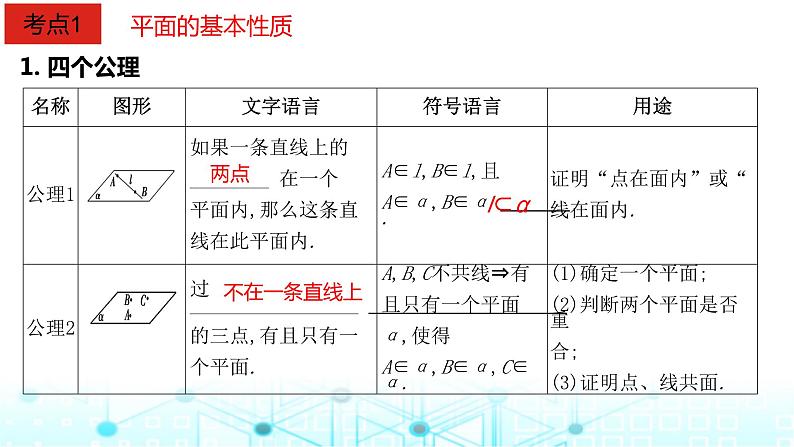
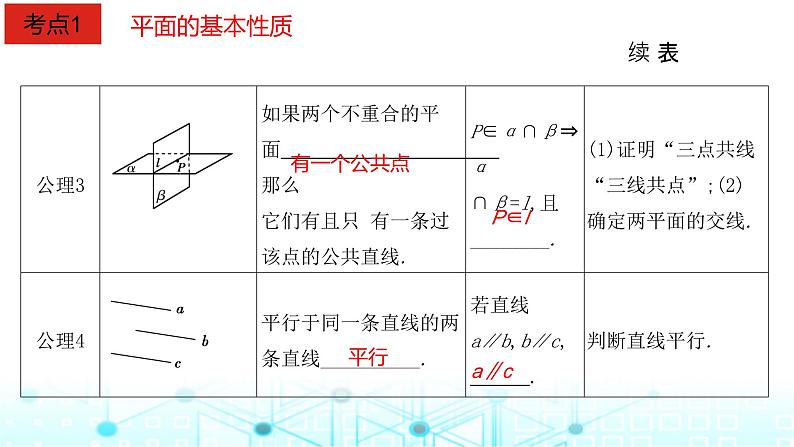
这是一份2024届人教A版高考数学一轮复习空间空间点直线平面之间的位置关系课件1,共40页。PPT课件主要包含了平面的基本性质,考点1,四个公理,l⊂α,不在一条直线上,有一个公共点,P∈l,a∥c,考点2,相等或互补等内容,欢迎下载使用。
2. 公理2的推论推论1 经过一条直线和 外一点,有且只有一个平面.推论2 经过两条 直线,有且只有一个平面.推论3 经过两条平行直线,有且只有一个平面.
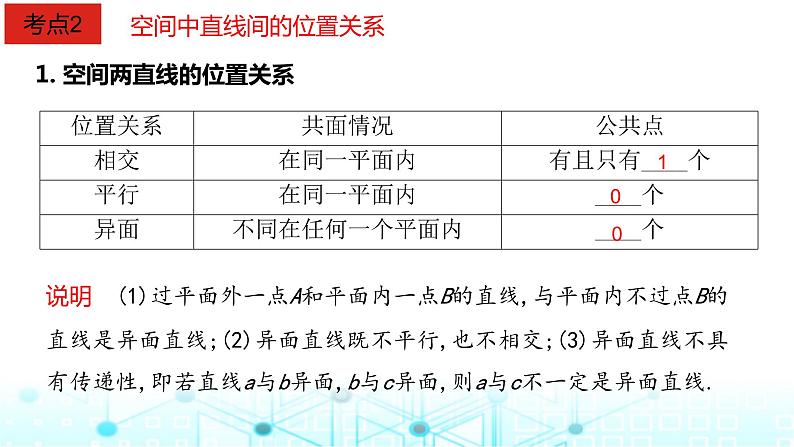
空间中直线间的位置关系
1. 空间两直线的位置关系
说明 (1)过平面外一点A和平面内一点B的直线,与平面内不过点B的直线是异面直线;(2)异面直线既不平行,也不相交;(3)异面直线不具有传递性,即若直线a与b异面,b与c异面,则a与c不一定是异面直线.
2. 等角定理空间中如果两个角的两边分别对应平行,那么这两个角____________.3. 异面直线所成的角(1)定义:设a,b是两条异面直线,如图,经过空间任一点O,分别作直线a'∥a,b'∥b,a'和b'所成的_____________叫作异面直线a与b所成的角(或夹角).特别地,当两条异面直线所成的角是_______时,则称这两条直线互相垂直.(2)范围: .
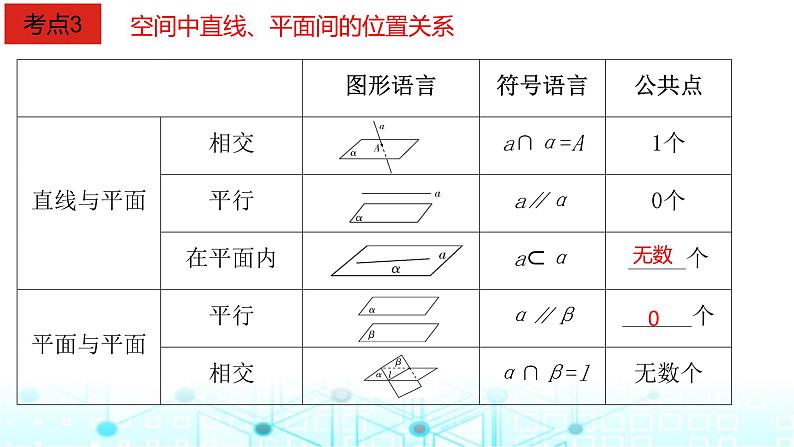
空间中直线、平面间的位置关系
理解自测1.判断正误(正确的打“√”,错误的打“✕”).(1)过三点确定一个平面. ( )(2)梯形一定是平面图形. ( )(3)若两个平面有三个公共点,则这两个平面重合.( ) (4)没有公共点的两条直线是异面直线.( )(5)若两个不重合的平面α,β有一条公共直线a,则平面α,β相交,并记作α∩β=a.( )(6)若三条直线a,b,c两两平行且分别交直线l于A,B,C三点,则这四条直线共面.( )
2.[教材改编]若直线a不平行于平面α,且a⊄α,则下列结论成立的是 ( )A.α内的所有直线与a异面B.α内不存在与a平行的直线C.α内存在唯一的直线与a平行D.α内的直线与a都相交3.如图,α∩β=l,A,B∈α,C∈β,且C∉l,直线AB∩l=M,过A,B,C三点的平面记作γ,则γ与β的交线必通过 ( )A.点A B.点BC.点C但不过点M D.点C和点M
平面的基本性质及应用
1.典例 [2020全国卷Ⅱ][理]设有下列四个命题:p1:两两相交且不过同一点的三条直线必在同一平面内.p2:过空间中任意三点有且仅有一个平面.p3:若空间两条直线不相交,则这两条直线平行.p4:若直线l⊂平面α,直线m⊥平面α,则m⊥l.则下述命题中所有真命题的序号是 . ①p1∧p4 ②p1∧p2③¬p2∨p3④¬p3∨¬p4
解析 对于p1,由题意设直线l1∩l2=A,l2∩l3=B,l1∩l3=C,则A,B,C三点不共线,所以此三点确定一个平面α,则A∈α,B∈α,C∈α,所以AB⊂α,BC⊂α,CA⊂α,即l2⊂α,l3⊂α,l1⊂α,所以p1是真命题.对于p2,当A,B,C三点不共线时,过A,B,C三点有且仅有一个平面;当A,B,C三点共线时,过A,B,C的平面有无数个,所以p2是假命题,¬p2是真命题.对于p3,若空间两条直线不相交,则这两条直线可能平行,也可能异面,所以p3是假命题,¬p3是真命题.对于p4,很显然p4是真命题,则¬p4是假命题.故p1∧p4为真命题,p1∧p2为假命题,¬p2∨p3为真命题,¬p3∨¬p4为真命题.综上可知,真命题的序号是①③④.
2.典例 [截面交线问题]已知ABCD-A1B1C1D1是正方体,在图 (1)中,E,F分别是D1C1,B1B的中点,画出图 (1)(2)中有阴影的平面与平面ABCD的交线,并给出证明.
解析 在图(1)中,过点E作EN∥B1B交CD于点N,连接NB并延长交EF的延长线于点M,连接AM,则AM即为有阴影的平面与平面ABCD的交线.在图(2)中,过点C1作C1M∥A1B交DC的延长线于点M,连接BM,则BM即为有阴影的平面与平面ABCD的交线.
证明如下:在图(1)中,因为直线EN∥BF,所以B,N,E,F四点共面,因此EF与BN相交,交点为M.因为M∈EF,且M∈NB,而EF⊂平面AEF,NB⊂平面ABCD,所以M是平面ABCD与平面AEF的公共点.又因为点A是平面AEF和平面ABCD的公共点,故AM为两平面的交线;在图(2)中,C1M在平面DCC1D1内,因此C1M与DC的延长线相交,交点为M,则点M为平面A1C1B与平面ABCD的公共点,又点B是这两个平面的公共点,因此直线BM是两平面的交线.
方法技巧 1.证明点共线问题的常用方法
2.证明线共点问题的常用方法先证两条直线交于一点,再证明第三条直线经过该点.
3.证明点、直线共面问题的常用方法
3.变式 (1)以下四个命题中,正确命题的个数是 ( )①不共面的四点中,其中任意三点不共线;②若点A,B,C,D共面,点A,B,C,E共面,则A,B,C,D,E共面;③若直线a,b共面,直线a,c共面,则直线b,c共面;④依次首尾相接的四条线段必共面.A.0B.1C.2D.3(2)如图所示,ABCD-A1B1C1D1是长方体,O是B1D1的中点,直线A1C交平面AB1D1于点M,则下列结论正确的是( )A.A,M,O三点共线 B.A,M,O,A1不共面C.A,M,C,O不共面 D.B,B1,O,M共面
解析 (1)①显然是正确的,可用反证法证明;②若A,B,C三点共线,则A,B,C,D,E五点不一定共面,②不正确;③直线b,c也可能异面,故③不正确;④空间四边形中四条线段不共面,故④不正确.(2)由ABCD-A1B1C1D1是长方体,易得A1,C1,A,C四点共面.∵M∈A1C,A1C⊂平面ACC1A1,∴M∈平面ACC1A1,又M∈平面AB1D1,∴M在平面ACC1A1与平面AB1D1的交线上.同理O在平面ACC1A1与平面AB1D1的交线上,∴A,M,O三点共线,故A正确,B,C错误.对于D,BB1与OM异面,故D不正确.
空间两直线的位置关系
4.典例 已知平面α,β,γ两两垂直,直线a,b,c满足a⊂α,b⊂β,c⊂γ,则直线a,b,c可能满足以下关系:①两两相交;②两两平行;③两两异面.其中所有正确结论的编号是 ( ) A.①②B.②③ C.①③ D.①②③解析 对于①,如图(1),当α∩β=a,α∩γ=c,β∩γ=b时,直线a,b,c两两相交,所以①正确;对于②,如图(2),假设a∥b∥c,α∩γ=m,易证m∥b,因为平面α,β,γ两两垂直,所以m⊥β,因为b⊂β,所以m⊥b,这与m∥b相矛盾,所以假设不成立,所以②不正确;对于③,如图(3),当a,b,c分别平行于平面α与β,β与γ,α与γ的交线时,a,b,c两两异面,所以③正确.综上,正确结论的编号是①③.
5.典例 [2019全国卷Ⅲ][理]如图,点N为正方形ABCD的中心,△ECD为正三角形,平面ECD⊥平面ABCD,M是线段ED的中点,则 ( )A.BM=EN,且直线BM,EN是相交直线B.BM≠EN,且直线BM,EN是相交直线C.BM=EN,且直线BM,EN是异面直线D.BM≠EN,且直线BM,EN是异面直线
6.变式 若直线l1和l2是异面直线,l1在平面α内,l2在平面β内,l是平面α与平面β的交线,则下列命题正确的是 ( )A.l与l1,l2都不相交B.l与l1,l2都相交C.l至多与l1,l2中的一条相交D.l至少与l1,l2中的一条相交
解析 A项,如左图所示,l2与l相交,故A项错误;B项,如左图所示,l1∥l,l1与l不相交,故B项错误;C项,如右图所示,l与l1,l2都相交,故C项错误;D项,假设l与l1,l2不相交,因为l与l1共面且l与l2共面,所以l1∥l∥l2,这与l1,l2为异面直线矛盾,故l至少与l1,l2中的一条相交,故D项正确.
求异面直线所成的角
方法技巧 求异面直线所成角的方法1.平移法具体步骤如下:
立体几何中的动态问题
角度1 判断动点轨迹的形状9.典例 [2021福州三中6月检测]在正方体ABCD-A1B1C1D1中,P是侧面BB1C1C内一动点.若P到直线BC的距离等于它到直线C1D1的距离,则动点 P的轨迹所在的曲线是 ( ) A.直线 B.椭圆 C.双曲线 D.抛物线解析 如图,连接C1P,过点P作PE⊥BC,E为垂足,易知PC1就是点P到直线C1D1的距离,则PC1=PE, (点P到定点C1的距离与到定直线BC的距离相等)所以动点P在侧面BB1C1C内的一段抛物线上.
方法技巧 立体几何中的动态问题主要包括空间动点轨迹的判断、求轨迹的长度或动角的范围等.解题时一般先判断动点运动的轨迹形态,再计算轨迹长度或求解动角的取值范围.
11.变式 [2021湖北联考]在三棱锥P-ABC 中,PA⊥AB,PA=4,AB=3,二面角P-AB-C 的大小为30°,在侧面△PAB内(含边界)有一个动点M,满足M到PA的距离与M到平面ABC的距离相等,则点M的轨迹的长度为 . 解析 如图,作MO⊥平面ABC,垂足是O,作MD∥PA,交AB于点D.连接OD,则∠MDO是二面角P-AB-C的平面角,所以∠MDO=30°,所以MD=2MO=2d(d是动点M到PA的距离).
相关课件
这是一份2024届人教A版高考数学一轮复习空间空间点直线平面之间的位置关系课件2,共36页。PPT课件主要包含了平面的基本性质,考点1,四个公理,l⊂α,不在一条直线上,有一个公共点,P∈l,a∥c,考点2,相等或互补等内容,欢迎下载使用。
这是一份空间点、直线、平面之间的位置关系-高考数学一轮复习课件PPT,共21页。
这是一份人教A版高考数学一轮总复习第7章第2节空间点、直线、平面之间的位置关系教学课件,共56页。









