2024届人教A版高考数学一轮复习空间向量及其应用课件

这是一份2024届人教A版高考数学一轮复习空间向量及其应用课件，共60页。PPT课件主要包含了空间向量及其运算，考点1，aλb，不共线，pxa+yb，pxa+yb+zc，空间向量的应用，考点2，n·m0，cosab等内容，欢迎下载使用。
1.空间向量的概念以及空间向量的加、减、数乘、数量积运算及其坐标表示是平面向量的类比推广. 2 .空间向量的三个定理
a1b1+a2b2+a3b3
a1=λb1,a2=λb2,a3=λb3(λ∈R)
a1b1+a2b2+a3b3=0
1. 直线的方向向量和平面的法向量
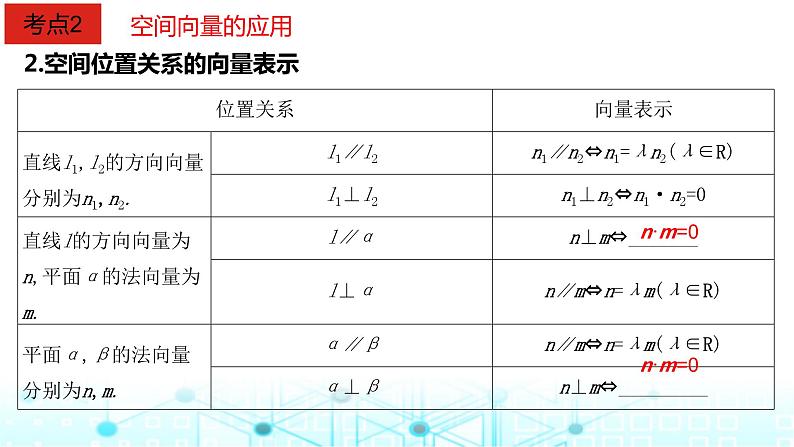
2.空间位置关系的向量表示
3. 直线与平面所成的角(1)
(2)线面角θ的取值范围:　　 　. (3)最小角定理:平面的斜线和它在平面内的射影所成的角是这条斜线和这个平面内任一条直线所成角中最小的角.
4. 二面角如图,在二面角α-l-β的棱l上任取一点P,以点P为垂足,在半平面α,β内分别作垂直于棱l的射线PA和PB,则射线PA和PB构成的∠APB叫作二面角α-l-β的平面角.二面角的大小可以用它的平面角来度量,二面角的平面角是多少度,就说这个二面角是多少度.我们规定,二面角的取值范围是________.平面角是直角的二面角叫作直二面角.
5. 利用向量法求空间角
理解自测1.在空间直角坐标系中,A(1,1,-2),B(1,2,-3),C(-1,3,0),D(x,y,z)(x,y,z∈R),若A,B,C,D四点共面,则 (　　)　　　　　　　　　A.2x+y+z=1B.x+y+z=0 C.x-y+z=-4 D.x+y-z=02.[广东高考][理]已知向量a=(1,0,-1),则下列向量中与a成60°夹角的是(　　)A.(-1,1,0) B.(1,-1,0) C.(0,-1,1) D.(-1,0,1)
利用向量法证明平行与垂直问题
1.典例 如图,在矩形ABCD中,AB=2BC,P,Q分别为线段AB,CD的中点,EP⊥平面ABCD.(1)求证:AQ∥平面CEP.(2)求证:平面AEQ⊥平面DEP.
方法技巧 1.利用空间向量证明平行问题的方法
2.利用空间向量证明垂直问题的方法
注意 用向量法证明平行与垂直问题时,要注意解题的规范性.如证明线面平行时,需要说明一条直线在平面内,另一条直线在平面外.
角度1 求异面直线所成的角详见P160考向3.角度2　求线面角2.典例 [2020浙江高考]如图,在三棱台ABC-DEF中,平面ACFD⊥平面ABC,∠ACB=∠ACD=45°,DC=2BC.(Ⅰ)证明:EF⊥DB.(Ⅱ)求直线DF与平面DBC所成角的正弦值.
方法技巧 求直线与平面所成角的方法
3.变式 [2020新高考卷Ⅰ]如图,四棱锥P-ABCD的底面为正方形,PD⊥底面ABCD.设平面PAD与平面PBC的交线为l.(1)证明:l⊥平面PDC.(2)已知PD=AD=1,Q为l上的点,求PB与平面QCD所成角的正弦值的最大值..
解析 (1)因为PD⊥底面ABCD,所以PD⊥AD.又底面ABCD为正方形,所以AD⊥DC.又PD∩DC=D,PD,DC⊂平面PDC,因此AD⊥平面PDC.因为AD∥BC,AD⊄平面PBC,BC⊂平面PBC,所以AD∥平面PBC.又AD⊂平面PAD,平面PBC∩平面PAD=l,所以l∥AD.因此l⊥平面PDC.
角度3　求二面角4.典例 [2021全国卷乙][理]如图,四棱锥P-ABCD的底面是矩形,PD⊥底面ABCD,PD=DC=1,M为BC的中点,且PB⊥AM.(1)求BC;(2)求二面角A-PM-B的正弦值.
5.变式 [2021新高考卷Ⅰ]如图,在三棱锥A-BCD中,平面ABD⊥平面BCD,AB=AD,O为BD的中点.(1)证明:OA⊥CD.(2)若△OCD是边长为1的等边三角形,点E在棱AD上,DE=2EA,且二面角E-BC-D的大小为45°,求三棱锥A-BCD的体积.
方法技巧 求空间距离常用的方法
立体几何中的探索性问题
角度1　条件追溯型如果已知的是问题的结论,要求的是问题的条件,这种试题为条件追溯型试题.
解析 (1)因为PA⊥平面ABCD,CD⊂平面ABCD,所以PA⊥CD.又AD⊥CD,AD∩PA=A,AD,PA⊂平面PAD,所以CD⊥平面PAD.(2)过A作AD的垂线交BC于点M.因为PA⊥平面ABCD,所以PA⊥AM,PA⊥AD.以A为坐标原点,分别以AM,AD,AP所在直线为x轴,y轴,z轴,建立如图所示的空间直角坐标系,(建系)则A(0,0,0),B(2,-1,0),C(2,2,0),D(0,2,0),P(0,0,2).因为E为PD的中点,所以E(0,1,1).
方法技巧 1.求解立体几何中的探索性问题的策略
2.求解立体几何中探索性问题的技巧(1)涉及线段上点的位置的探索性问题,所求点多为中点或三等分点中某一个,也可以根据相似知识找点,求解时注意三点共线条件的应用. (2)借助空间直角坐标系,把几何对象上动点的坐标用参数表示出来,根据题设得到相应的方程或方程组.若方程或方程组有满足题设要求的解,则通过参数的值反过来确定几何对象的位置;若方程或方程组没有满足题设要求的解,则表示满足题设要求的几何对象不存在.
立体几何中的翻折问题
将平面图形沿一条或几条线段折起,使其成为空间图形,这类问题称为立体几何中的翻折问题,翻折问题常与空间中的平行、垂直以及空间角相结合命题.11.典例 [2019全国卷Ⅲ][理]图（1）是由矩形ADEB,Rt△ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°.将其沿AB,BC折起使得BE与BF重合,连接DG,如图（2）.(1)证明:图（1）中的A,C,G,D四点共面,且平面ABC⊥平面BCGE.(2)求图（2）中的二面角B-CG-A的大小.
解析 (1)由已知得AD∥BE,CG∥BE, (位于“折痕”同侧的点、线、面之间的位置关系不变)所以AD∥CG,故AD,CG确定一个平面,从而A,C,G,D四点共面.由已知得AB⊥BE,AB⊥BC, (与“折痕”垂直的线段,翻折前后垂直关系不变)又BC∩BE=B,BC,BE⊂平面BCGE,故AB⊥平面BCGE.又AB⊂平面ABC,所以平面ABC⊥平面BCGE.
方法技巧 翻折问题的解题策略策略:(1)画好两个图——折叠前的平面图和折叠后的立体图;(2)分析好两个关系——折叠前后哪些位置关系和数量关系发生了变化,哪些没有发生变化.一般地,位于“折痕”同侧的点、线、面之间的位置和数量关系不变,而位于“折痕”两侧的点、线、面之间的位置关系会发生变化.技巧:(1)与折痕垂直的线段,翻折前后垂直关系不改变(常用于翻折后构成二面角的平面角);(2)与折痕平行的线段,翻折前后平行关系不改变.
解析 (1)由题意知,PA⊥AC,(与折痕垂直的线段,翻折前后垂直关系不变)即∠PAC=90°,∵AC=AD,PC=PD,PA=PA,∴△PAC≌△PAD.(由平面几何知识证明两个三角形全等)∴∠PAD=∠PAC=90°,∴PA⊥AD.又AC∩AD=A,AC,AD⊂平面ACD,∴PA⊥平面ACD.∵CD⊂平面ACD,∴CD⊥PA.