2024届人教A版高考数学一轮复习空间几何体的结构视图表面积和体积课件

这是一份2024届人教A版高考数学一轮复习空间几何体的结构视图表面积和体积课件，共60页。PPT课件主要包含了空间几何体的结构，考点1，多面体的结构特征，平行四边形，直角三角形，直角梯形，垂直于底面，等腰三角形，考点2，正视图等内容，欢迎下载使用。
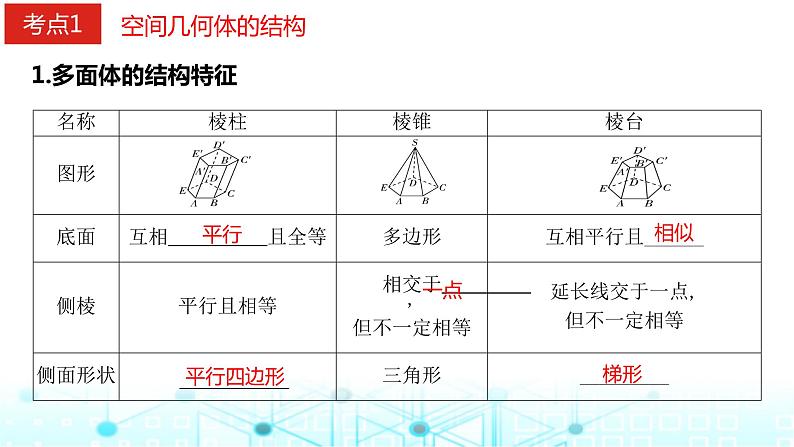
规律总结1.特殊的棱柱和棱锥(1)侧棱垂直于底面的棱柱叫作直棱柱,底面是正多边形的直棱柱叫作正棱柱.反之,正棱柱的底面是正多边形,侧棱垂直于底面,侧面是矩形.(2)底面是正多边形,顶点在底面的射影是底面正多边形的中心的棱锥叫作正棱锥.特别地,各棱长均相等的正三棱锥叫作正四面体.反之,正棱锥的底面是正多边形,且顶点在底面的射影是底面正多边形的中心.
2.正棱锥中的直角三角形已知正棱锥,如图(以正四棱锥为例),其高为PO,底面为正方形,作PE⊥CD于E,则PE为斜高,连接OC,OE,则(1)斜高、侧棱长、底面边长的一半构成直角三角形,如图中Rt△PEC;(2)斜高、高、斜高在底面的射影长构成直角三角形,如图中Rt△POE;(3)侧棱长、高、侧棱在底面的射影长构成直角三角形,如图中Rt△POC;(4)斜高在底面的射影长、侧棱在底面的射影长、底面边长的一半构成直角三角形,如图中Rt△OEC.
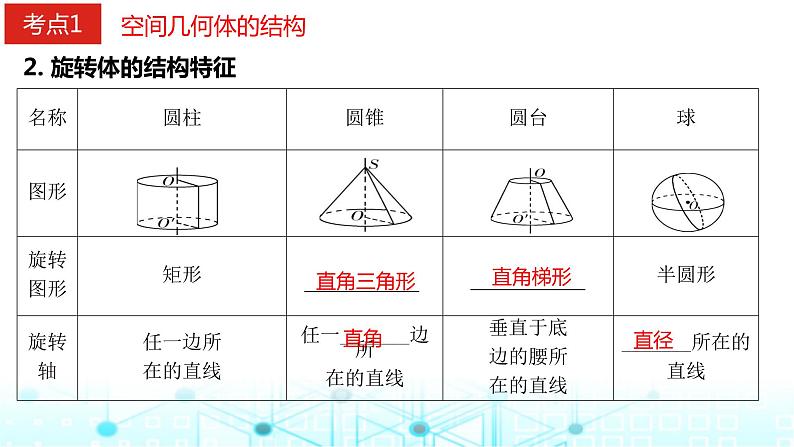
2. 旋转体的结构特征
规律总结 球的截面的性质(1)球的任何截面都是圆面;(2)球心和截面(不过球心)圆心的连线垂直于截面.
空间几何体的三视图与直观图
1. 三视图的定义几何体的 、侧视图和_________统称为几何体的三视图.三视图中的正视图、侧视图、俯视图分别是从几何体的正前方、 正左方、正上方观察几何体画出的轮廓线.注意 (1)画三视图时,重叠的线只画一条,能看见的线用实线表示,不能看见的线用虚线表示.(2)同一物体,若放置的位置不同,则所得的三视图可能不同.
2. 三视图的长度特征“长对正、宽相等、高平齐”,即正视图和俯视图的长对正,侧视图和俯视图的宽相等,正视图和侧视图的高平齐.3. 直观图(1)画法:常用斜二测画法.(2)规则:a.原图形中x轴、y轴、z轴两两垂直,直观图中,x'轴、y'轴的夹角为45°(或135°),z'轴与x'轴和y'轴所在平面垂直.b.原图形中平行于坐标轴的线段,直观图中仍平行于坐标轴.
c.平行于x轴和z轴的线段在直观图中保持原长度 _____,平行于y轴的线段长度在直观图中变为原来的_______.(3)用斜二测画法画出的平面图形的直观图的面积与原图形面积的关系:S直观图= _________S原图形. 注意 用斜二测画法画直观图时,原图中不与坐标轴平行的直线段可以先画出线段的端点再连线,原图中的曲线段可以通过取一些关键点,作出在直观图中的相应点后,用平滑的曲线连接而画出.
空间几何体的表面积和体积
1. 圆柱、圆锥、圆台的侧面展开图及侧面积公式
说明 圆柱、圆锥、圆台的侧面积公式间的关系:S圆柱侧=2πrl S圆台侧=π(r+r＇)l S圆锥侧=πrl.
2. 空间几何体的表面积与体积
理解自测1.判断正误(正确的打“√”,错误的打“✕”).(1)棱柱的侧棱都相等,侧面都是全等的平行四边形.( )(2)在四棱柱中,若两个过相对侧棱的截面都垂直于底面,则该四棱柱为直四棱柱.( )(3)棱台的侧棱延长后交于一点.( )(4)以直角梯形的一腰所在直线为轴旋转一周所得的旋转体是圆台.( )(5)圆柱、圆锥、圆台的底面都是圆面. ( )(6)以直角三角形的一边所在直线为轴旋转一周所得的旋转体是圆锥.( )(7)圆柱的一个底面积为S,侧面展开图是一个正方形,那么这个圆柱的侧面积是2πS.( )
2.[易错题]如图,长方体ABCD-A'B'C'D'被截去一部分,其中EH∥A'D',剩下的几何体是( ) A.棱台　　B.四棱柱 C.五棱柱 D.六棱柱3.[易错题]圆柱的侧面展开图是边长为6π和4π的矩形,则圆柱的表面积为　　 　　. 4.有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图).∠ABC=45°,AB=AD=1,DC⊥BC,则这块菜地的面积为　　 　　.
24π2+18π或24π2+8π
1.典例 (1)给出下列命题:①在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线;②一个平面截圆锥,得到一个圆锥和一个圆台;③圆锥的所有轴截面都是全等的等腰三角形;④圆锥的轴截面是所有过顶点的截面中,面积最大的一个;⑤三棱锥的四个面中最多有三个直角三角形.其中正确命题的个数是(　　)　　　　A.0B.1 C.2 D.3(2)如图,正三棱锥A-BCD的底面边长为a,侧棱长为2a,点E,F分别为AC,AD上的动点,则截面△BEF周长的最小值为　　　　. 
解析 (1) ①只有当这两点的连线平行于轴时才是母线,故①不正确;②只有平行于圆锥底面的平面截圆锥,才能得到一个圆锥和一个圆台,故②不正确;③正确;④因为圆锥的母线长一定,根据三角形面积公式知,过圆锥顶点的截面中,两条母线的夹角的正弦值越大,截面面积就越大,所以当轴截面中两条母线的夹角为钝角时,轴截面的面积就不是最大的,故④不正确;⑤三棱锥的四个面中最多有四个直角三角形,故⑤不正确.
方法技巧 求解空间几何体表面上两点间的最短距离问题或两条(多条)线段长度和的最小值问题常归结为求平面两点间的最短距离问题,解决此类题的方法就是先把多面体侧面展开成平面图形,再用平面几何的知识去求解.注意 (1)解决展开问题的关键是明确需要展开立体图形中的哪几个面(有时需要分类讨论),以及利用哪些平面几何定理来解决对应的立体图形问题.(2)注意立体图形展开前后线段与角度哪些会改变,哪些不会变.
空间几何体的三视图
3.典例 [2021全国卷甲][文] 在一个正方体中,过顶点A的三条棱的中点分别为E,F,G.该正方体截去三棱锥A-EFG后,所得多面体的三视图中,正视图如图所示,则相应的侧视图是(　)
解析 根据题目条件以及正视图可以得到该几何体的直观图,如图,结合选项可知该几何体的侧视图为选项D所示的图形.
方法技巧 1.三视图与直观图的常见题型及求解策略(1)由直观图求三视图.注意正视图、侧视图和俯视图的观察方向,同时也要注意看到的轮廓线用实线表示,看不到的轮廓线用虚线表示.(2)由几何体的部分三视图画出剩下的三视图.先根据已知的部分三视图,推测、还原直观图的可能形式,然后找剩下部分三视图的可能形式.做选择题时,也可以将选项代入,看给出的部分三视图是否符合要求.
(3)由三视图还原为几何体.要遵循以下三步:①看视图,明关系;②分部分,想整体;③综合起来,定整体.2.根据几何体的三视图判断几何体的结构特征(1)三视图为三个三角形,一般对应三棱锥;(2)三视图为两个三角形,一个四边形,一般对应四棱锥;(3)三视图为两个三角形,一个圆,一般对应圆锥;(4)三视图为一个三角形,两个四边形,一般对应三棱柱;(5)三视图为两个四边形,一个圆,一般对应圆柱.
4.变式 [2020全国卷Ⅱ]如图是一个多面体的三视图,这个多面体某条棱的一个端点在正视图中对应的点为M,在俯视图中对应的点为N,则该端点在侧视图中对应的点为 (　)A.EB.FC.GD.H解析 由三视图知,该几何体是由两个长方体组合而成的,其直观图如图所示,由图知该端点在侧视图中对应的点为E.
求空间几何体的表面积（侧面积）
角度1　求空间几何体的表面积
5.典例 [2018全国卷Ⅰ][文]已知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为 (　　)
方法技巧 求空间几何体的表面积的常见类型及解题思路
S2=4×6a2+2×(10+8)=24a2+36,S3=4×6a2+2×(10+6)=24a2+32.当拼成四棱柱时有三种情况,如图④⑤⑥所示,表面积分别为S4=4×6a2+2×(8+6)=24a2+28,S5=4×6a2+2×(10+8)=24a2+36,S6=4×6a2+2×(10+6)=24a2+32.
求空间几何体的体积
角度1　求空间几何体的体积
8.典例 [2018天津高考][文]如图,已知正方体ABCD-A1B1C1D1的棱长为1,则四棱锥A1-BB1D1D的体积为　　　　. 
方法技巧 求空间几何体体积的常用方法
角度2　体积的最值问题
方法技巧 求解体积的最值问题的方法(1)几何法:根据几何体的结构特征,先确定体积表达式中的常量与变量,然后利用几何知识判断变量什么情况下取得最值,从而确定体积的最值.(2)代数法:先设变量,求出几何体的体积表达式,然后转化为函数最值问题求解即可.
与球有关的切、接问题
角度1　外接球问题解决外接球问题的关键是抓住外接球的特点,即球心到多面体的顶点的距离等于球的半径.
与球有关的切、接问题
方法技巧 1.求几何体外接球半径的思路(1)利用球的截面性质求解.如图所示,设球O的半径为R,截面圆O'的半径为r,M为截面圆上任一点,球心O到截面圆O'的距离为d,则在Rt△OO'M中,OM2=OO'2+O'M2,即R2=d2+r2.(2)将几何体补形成长方体(或正方体),利用几何体与长方体(或正方体)共有外接球的特征,由外接球的直径等于长方体(或正方体)的体对角线长求解.如三条侧棱互相垂直的三棱锥,当侧棱长相等时可补形成正方体,当侧棱长不相等时可补形成长方体.
2. 确定几何体外接球球心的常用结论(1)长方体或正方体的外接球的球心是其体对角线的中点;(2)直三棱柱的外接球的球心是上、下底面三角形外心连线的中点;(3)正棱锥的外接球的球心在其高上,具体位置可通过建立直角三角形运用勾股定理计算得到.
角度2　内切球问题求解多面体的内切球问题,一般是将多面体分割为以内切球球心为顶点,多面体的各侧面为底面的棱锥,利用多面体的体积等于分割后各棱锥的体积之和,求内切球的半径.12.典例 [2020全国卷Ⅲ][文]已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为　　　　. 
方法技巧 1.解与球有关的切、接问题的思维流程通法是作截面,将空间几何问题转化为平面几何问题求解,其解题的思维流程如下:
14.典例 [2019全国卷Ⅲ][文]学生到工厂劳动实践,利用3D打印技术制作模型.如图,该模型为长方体ABCD-A1B1C1D1挖去四棱锥O-EFGH后所得的几何体,其中O为长方体的中心,E,F,G,H分别为所在棱的中点,AB=BC=6 cm,AA1=4 cm.3D打印所用原料密度为0.9 g/cm3.不考虑打印损耗,制作该模型所需原料的质量为　　　　 g. 
16.典例 [2019全国卷Ⅱ][文]中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(如左图).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.右图是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有　　　　个面,其棱长为　　　　. 
立体几何中的截面问题
方法技巧 作截面的三种常用方法一是直接法,解题关键是截面上的点在几何体的棱上,且两两在一个平面内,可以直接借助P154公理1作出截面.二是作平行线法,解题关键是截面与几何体的两个平行平面相交,或者截面上有一条直线与几何体的某一个面平行,可借助线面平行的性质定理和面面平行的性质定理作出截面.三是延长交线得交点,解题关键是截面上的点中至少有两个点在几何体的同一个面上,可通过由作延长线得到的交点辅助得出截面与立体几何图形的交点,进而得交线和截面图形.
1.正方体的基本截面用一个平面截正方体,可以得到的截面形状如下:
在这里需要给大家强调一下,正方体的斜截面不会出现以下几种图形:直角三角形、钝角三角形、直角梯形、正五边形.2.圆柱体的基本截面用一个平面截圆柱,可以得到的截面形状如下:
19.变式 [2021江苏盐城模拟]在棱长为4的正方体ABCD-A1B1C1D1中,P,Q分别为棱A1D1,CC1的中点,过P,Q,A作正方体的截面,则截面多边形的周长是　　 　 　.解析 解法一(由特征点确定平行关系,进而得到截面)　由于P,Q,A三点不共线,因此可以确定一个过点P,Q,A的平面α,平面α与正方体ABCD-A1B1C1D1的各个面的交线形成的多边形即所求的截面.如图,过Q作QM∥AP交BC于M,(根据特征点寻求平行线)易知Rt△A1AP∽Rt△CQM,所以∠APA1=∠CMQ,