2024届人教A版高考数学一轮复习第2章函数第5节指数与指数函数课件

这是一份2024届人教A版高考数学一轮复习第2章函数第5节指数与指数函数课件，共52页。PPT课件主要包含了xn＝a，有理数指数幂，没有意义，ar＋s，ars，arbr，0＋∞，减函数，增函数，四字程序等内容，欢迎下载使用。
考试要求：1．了解指数幂的拓展过程，掌握指数幂的运算性质．2．了解指数函数的实际意义，了解指数函数的概念．3．能画具体指数函数的图象，探索并理解指数函数的单调性与特殊点．
必备知识·回顾教材重“四基”
3.指数函数的概念一般地，函数y＝ax(a>0，且a≠1)叫做指数函数，其中指数x是自变量，定义域是R.形如y＝kax(k≠1)，y＝ax＋k(k∈R且k≠0，a>0且a≠1)的函数叫做指数型函数，不是指数函数．
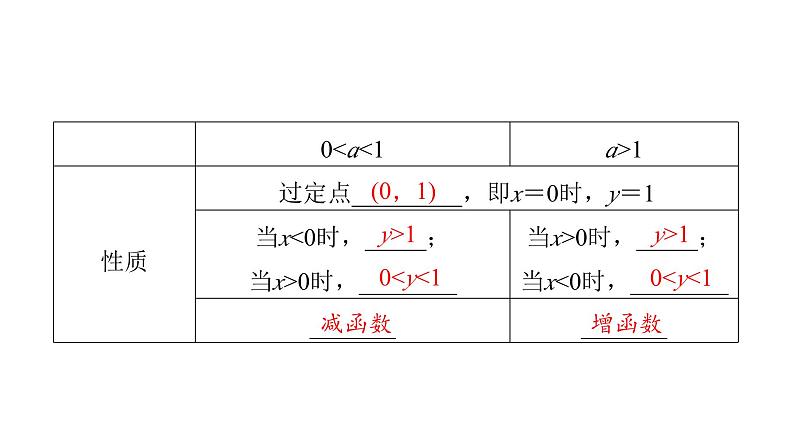
4．指数函数的图象与性质
3．函数y＝(a2－4a＋4)ax是指数函数，则a的值是(　　)A．4B．3C．2D．1B　解析：由指数函数的定义知a2－4a＋4＝1且a≠1，解得a＝3.
关键能力·研析考点强“四翼”
考点1　指数幂的化简与求值——基础性
考点2　指数函数的图象及应用——综合性
考点3　指数函数的性质及应用——应用性
1．解决这类问题要优先考虑将根式、分数指数幂统一为分数指数幂，以便利用法则计算．在运算过程中要先乘除后加减，负指数幂化成正指数幂的倒数，如果底数是负数，先确定符号；底数是小数，先化成分数；底数是带分数的，先化成假分数．2．这类问题的运算结果不能同时含有根号和分数指数，也不能既有分母又含有负指数，形式要力求统一．
例1　(1)已知函数f(x)＝4＋2ax-1(a>1且a≠1)的图象恒过点P，则点P的坐标是(　　)A．(1，6)B．(1，5)C．(0，5)D．(5，0)A　解析：当x＝1时，f(1)＝6，与a无关，所以函数f(x)＝4＋2ax-1的图象恒过点P(1，6)．故选A.
(2)若函数y＝|2x－1|的图象与直线y＝b有两个公共点，则b的取值范围为_________．(0，1)　解析：作出曲线y＝|2x－1|的图象与直线y＝b如图所示．由图象可得b的取值范围是(0，1)．
在本例(2)中，若将条件中的“有两个公共点”，改为“有一个公共点”，则结果如何？b≥1或b＝0　解析：作出曲线y＝|2x－1|的图象与直线y＝b如图所示．由图象可得b的取值范围是b≥1或b＝0.
指数函数图象的应用问题的求解方法(1)有关指数方程、不等式问题的求解，往往是利用相应的指数型函数图象，数形结合求解．(2)根据指数函数图象判断底数大小的问题，可以通过直线x＝1与图象的交点进行判断．
2．若曲线|y|＝2x＋1与直线y＝b没有公共点，则b的取值范围是_________．[－1，1]　解析：作出曲线|y|＝2x＋1的图象，如图所示，要使该曲线与直线y＝b没有公共点，只需－1≤b≤1.
比较幂的大小的方法(1)能化成同底数的先化成同底数幂，再利用单调性比较大小．(2)不能化成同底数的，一般引入“1”等中间量比较大小．
解简单指数不等式的方法先利用幂的运算性质化为同底数幂，再利用单调性转化为一般不等式求解，要注意底数a的取值范围，并在必要时进行分类讨论．
求函数f(x)＝ag(x)单调性的方法(1)先将f(x)＝ag(x)视为是由y＝au与u＝g(x)复合而成的．(2)分别讨论函数y＝au与u＝g(x)的单调性，利用“同增异减”的方法得出函数f(x)＝ag(x)的单调性．
1．研究指数函数的性质与研究一般函数的定义域、单调性(区间)、奇偶性、最值(值域)等性质的方法一致．2．研究复合函数的单调性，要明确复合函数的构成，借助“同增异减”，将问题归结为内层函数相关的问题加以解决．
2．已知函数y＝f(x)的定义域为R，y＝f(x＋1)为偶函数，对任意x1，x2，当x1>x2≥1时，f(x)单调递增，则关于a的不等式f(9a＋1)