2024届人教A版高考数学一轮复习第4章三角函数第4节函数y＝Asin(ωxφ)的图象及简单应用课件

这是一份2024届人教A版高考数学一轮复习第4章三角函数第4节函数y＝Asin(ωxφ)的图象及简单应用课件，共60页。PPT课件主要包含了ωx＋φ，四字程序等内容，欢迎下载使用。

考试要求：1．结合具体实例，了解函数y＝A sin (ωx＋φ)的实际意义．2．能借助图象理解参数A，ω，φ的意义，了解参数的变化对函数图象的影响．3．会用三角函数解决一些简单的实际问题，体会三角函数是描述周期变化现象的重要函数模型．
必备知识·回顾教材重“四基”
一、教材概念·结论·性质重现1．y＝A sin (ωx＋φ)的有关概念
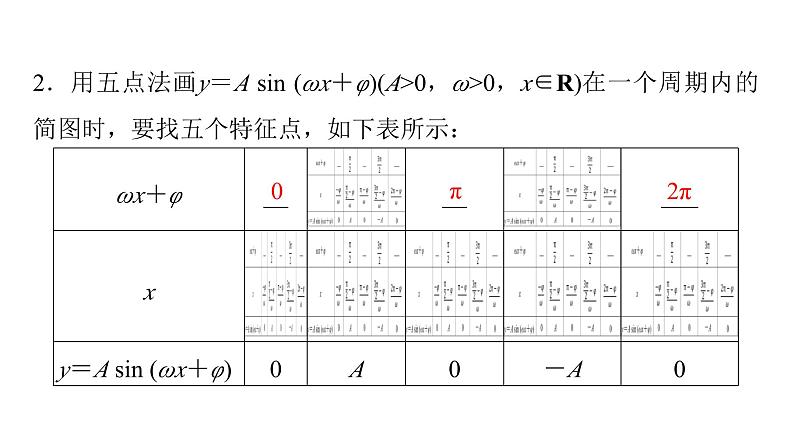
2．用五点法画y＝A sin (ωx＋φ)(A>0，ω>0，x∈R)在一个周期内的简图时，要找五个特征点，如下表所示：
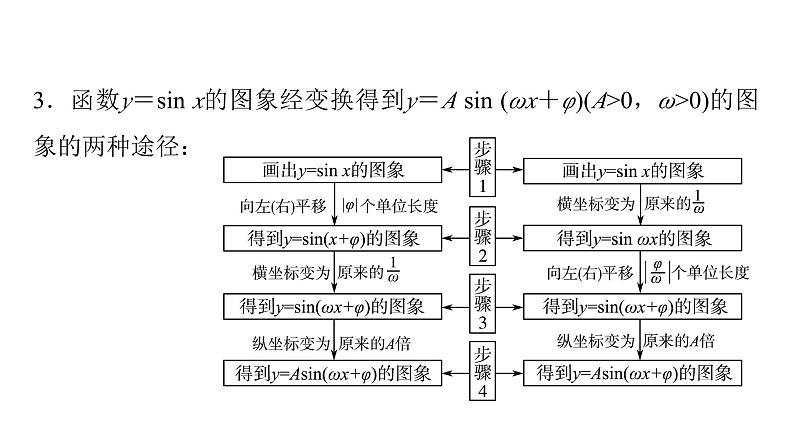
3．函数y＝sin x的图象经变换得到y＝A sin (ωx＋φ)(A>0，ω>0)的图象的两种途径：
5．函数y＝A sin(ωx＋φ)(A，ω，φ为常数，A＞0，ω＞0)在闭区间[－π，0]上的图象如图所示，则ω＝_________．
关键能力·研析考点强“四翼”
考点1　由图象确定y＝A sin (ωx＋φ)的解析式——基础性
考点2　函数y＝A sin (ωx＋φ)的图象变换——综合性
考点3　三角函数模型及其应用——应用性
考点4　三角函数图象与性质的综合问题——综合性
4．如图，某地一天6～14时的温度变化曲线近似满足函数T＝A sin (ωt＋φ)＋b，则这段曲线对应的函数解析式为____________．
1．由函数y＝sin x的图象通过变换得到y＝A sin (ωx＋φ)的图象有两条途径：“先平移后伸缩”与“先伸缩后平移”．要特别注意这两种情况下平移的单位长度．2．当变换前后解析式三角函数名称不同时，要注意利用诱导公式转化．
例2　如图，某大风车的半径为2米，每12秒旋转一周，它的最低点O离地面1米，点O在地面上的射影为A.风车圆周上一点M从最低点O开始，逆时针方向旋转40秒后到达P点，则点P到点A的距离与点P的高度之和为(　　)
三角函数模型的应用体现在两方面：一是已知函数模型求解数学问题；二是把实际问题抽象转化成数学问题，建立数学模型，再利用三角函数的有关知识解决问题．
1．筒车是我国古代发明的一种水利灌溉工具，因其经济又环保，至今还在农业生产中使用．假设在水流量稳定的情况下，筒车上的每一个盛水筒都做逆时针匀速圆周运动．现将筒车抽象为一个几何图形，如图所示，圆O的半径为4 m，P0在水平面上，盛水筒M从点P0处开始运动，OP0与水平面所成角为30°，且2分钟恰好转动1圈，则盛水筒M距离水面的高度H(单位：m)与时间t(单位：s)之间的函数关系式是(　　)
6 000　解析：作出函数简图如图：
1．研究y＝A sin (ωx＋φ)的性质时可将ωx＋φ视为一个整体，利用换元法和数形结合思想进行解题．2．方程根的个数可转化为两个函数图象的交点个数．
1．函数f(x)＝2sin (ωx＋φ)(ω＞0，|φ|＜π)的部分图象如图所示，则下列结论错误的是(　　)
一题N解·深化综合提“素养”
1．基于课程标准，解答本题一般需要提升运算求解能力、逻辑推理能力，体现逻辑推理、数学运算的核心素养．2．基于高考数学评价体系，本题涉及三角恒等变换、三角函数的图象与性质等知识，渗透了转化与化归思想方法，有一定的综合性，属于中低档难度题．