






2024届人教A版高考数学一轮复习第6章立体几何第6节立体几何中的向量方法__证明平行与垂直课件
展开考试要求:1.理解直线的方向向量及平面的法向量,能用向量语言表述线线、线面、面面的平行和垂直关系.2.能用向量方法证明立体几何中有关直线、平面位置关系的判定定理.
必备知识·回顾教材重“四基”
一、教材概念·结论·性质重现1.直线的方向向量与平面的法向量
方向向量和法向量均不为零向量且不唯一.
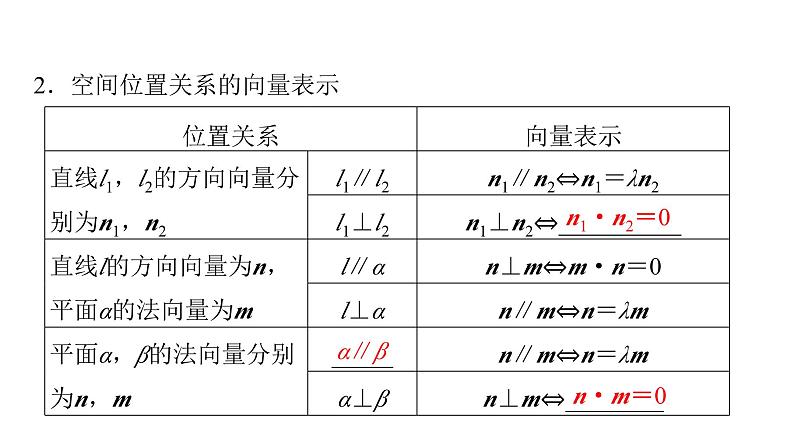
2.空间位置关系的向量表示
二、基本技能·思想·活动经验1.判断下列说法的正误,对的画“√”,错的画“×”.(1)直线的方向向量是唯一确定的.( )(2)平面的单位法向量是唯一确定的.( )(3)若两平面的法向量平行,则两平面平行.( )(4)若两直线的方向向量不平行,则两直线不平行.( )(5)若a∥b,则a所在直线与b所在直线平行.( )(6)若空间向量a平行于平面α,则a所在直线与平面α平行.( )
2.若直线l的方向向量a=(1,-3,5),平面α的法向量n=(-1,3,-5),则有( )A.l∥α B.l⊥αC.l与α斜交D.l⊂α或l∥αB 解析:由a=-n知,n∥a,则有l⊥α.故选B.
3.已知平面α,β的法向量分别为n1=(2,3,5),n2=(-3,1,-4),则( )A.α∥β B.α⊥βC.α,β相交但不垂直 D.以上均不对C 解析:因为n1≠λn2,且n1·n2=2×(-3)+3×1+5×(-4)=-23≠0,所以α,β既不平行,也不垂直.
4.如图,在正方体ABCD-A1B1C1D1中,O是底面正方形ABCD的中心,M是D1D的中点,N是A1B1的中点,则直线ON,AM的位置关系是________.
关键能力·研析考点强“四翼”
考点1 利用空间向量证明平行问题——基础性
考点2 利用空间向量证明垂直问题——应用性
考点3 利用空间向量解决探索性问题——应用性
例1 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,ABCD为正方形,△PAD是直角三角形,且PA=AD=2,E,F,G分别是线段PA,PD,CD的中点.求证:PB∥平面EFG.
证明:因为平面PAD⊥平面ABCD,ABCD为正方形,△PAD是直角三角形,且PA=AD,所以AB,AP,AD两两垂直,以A为坐标原点,建立如图所示的空间直角坐标系Axyz,
利用空间向量证明平行的方法
如图,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°角.求证:CM∥平面PAD.
证明:由题意知,CB,CD,CP两两垂直,以C为坐标原点,CB所在直线为x轴,CD所在直线为y轴,CP所在直线为z轴建立如图所示的空间直角坐标系Cxyz.
例2 如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB.求证:平面BCE⊥平面CDE.
1.利用空间向量证明垂直的方法2.向量法证明空间垂直、平行关系时,是以计算为手段,寻求直线上的线段对应的向量和平面的基向量、法向量的关系,关键是建立空间直角坐标系(或找空间一组基底)及平面的法向量.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.证明:(1)AE⊥CD;(2)PD⊥平面ABE.
证明:以A为原点,AB,AD,AP所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系Axyz.
例3 如图,在正方体ABCD-A1B1C1D1中,E是棱DD1的中点.在棱C1D1上是否存在一点F,使B1F∥平面A1BE?证明你的结论.
解:在棱C1D1上存在一点F(C1D1的中点),使B1F∥平面A1BE.证明如下:依题意,建立如图所示的空间直角坐标系,设正方体ABCD-A1B1C1D1的棱长为1,
向量法解决与垂直、平行有关的探索性问题的思路(1)根据题设条件中的垂直关系,建立适当的空间直角坐标系,将相关点、相关向量用坐标表示.(2)假设所求的点或参数存在,并用相关参数表示相关点的坐标,根据线、面满足的垂直、平行关系,构建方程(组)求解.若能求出参数的值且符合该限定的范围,则存在,否则不存在.
在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E,F分别是AB,PB的中点.(1)求证:EF⊥CD;
证明:由题意知,DA,DC,DP两两垂直.如图所示,以DA,DC,DP所在直线分别为x轴、y轴、z轴建立空间直角坐标系.
高考数学一轮复习第6章第6节立体几何中的向量方法——证明平行与垂直课件: 这是一份高考数学一轮复习第6章第6节立体几何中的向量方法——证明平行与垂直课件,共50页。PPT课件主要包含了平行或重合,方向向量a,α∥β,××√√,考点1考点2考点3等内容,欢迎下载使用。
人教A版高考数学一轮总复习第7章第6节立体几何中的向量方法——证明平行与垂直教学课件: 这是一份人教A版高考数学一轮总复习第7章第6节立体几何中的向量方法——证明平行与垂直教学课件,共56页。
人教B版高考数学一轮总复习41立体几何中的向量方法——证明平行与垂直习题课件: 这是一份人教B版高考数学一轮总复习41立体几何中的向量方法——证明平行与垂直习题课件,共40页。PPT课件主要包含了A组全考点巩固练,B组新高考培优练等内容,欢迎下载使用。












