高中数学2.2 基本不等式示范课课件ppt

这是一份高中数学2.2 基本不等式示范课课件ppt，共15页。

一 、 学 习 目 标(1)理解重要不等式 a²+b²≥2ab基本不等式的几何意义及代数意义；mage(2)能够利用基本不等式求简」二 、 自 学 指 导阅读课本P44--P46思考下列问题1、课本是如何推出基本不等式的?2、基本不等式表明了什么?3、如何证明基本不等式?4、使用基本不等式的条件有哪些?
三、新课讲授：你能给出不等式 a²+b²≥2ab 的证明吗? 证明： (作差法) a²+b²-2ab=(a-b)²当a≠b 时 (a-b)²>0当a=b 时 (a-b)²=0 所以(a-b)²≥0所以a²+b²≥2ab.
重要不等式：若a,b ∈R, 那 么a²+b²≥2ab(当且仅当a=b 时，取“=”号)◆文字叙述为：两数的平方和不小于积的2倍。
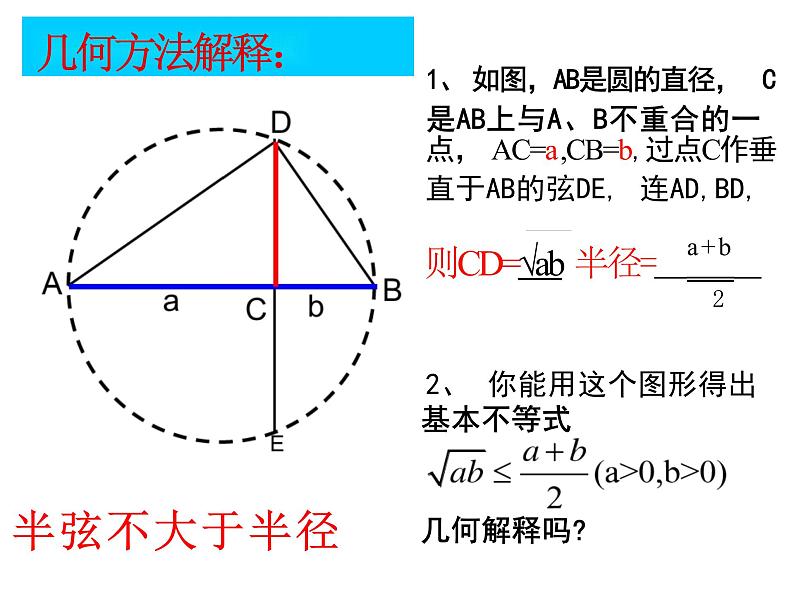
问题一如果a>0,b>0,我们用 √a,√b分别代替a,b,替换后得到： (√a)²+(√b)²≥2√a · √b 即：a+b≥2 √ab即： a+b ≥√ab(a>0,b>0)2问题二你能用几何方法解释这个不等式吗?
是AB上与A、B不重合的一点， AC=a ,CB=b,过点C作垂直于AB的弦DE, 连AD,BD,则CD=√ab 半径= a+b22、 你能用这个图形得出基本不等式
1、 如图，AB是圆的直径， C
基本不等式 剖析公式a+b ≥√ab(a>0,b>0)2(当且仅当a=b 时，取“=”号)· 我们把 叫做a,b的算术平均数，把 √ab 叫做a,b的几何平均数；· 文字叙述为：两个正数的算术平均数不小于它们的几 何平均数， 因此也叫均值不等式；· 从形的角度来看，基本不等式具有特定的几何意义； 从数的角度来看，基本不等式揭示了“和”与“积” 这两种结构间的不等关系；· 正用、逆用，注意成立的条件(1)a、b 是两个正数；(2)当且仅当a=b时“=”号成立。
变式：试判断 b 十 (a>0,b>0) 与2的大小关系?a b
例1.试判断x+ (x>0) 与2的大小关系?X
如果将条件 “x>0”去掉，上述结论是否仍然成立?
利用基本不等式解决最大 (小)值问题例2、已知X,y 都是正数，求证(1)如果积Xj 是定值P, 那么当x= y时，和x+y 有最小值 2√ P(2)如果和X+y 是定值S,那么当X=y 时，积Xy 有最大 值 ⊥s²小结：利用a +b≥2 √ab(a>0,b>0)求最值时要注意下面三条：(1)一正：各项均为正数(2) 二定：两个正数积为定值，和有最小值。两个正数和为定值，积有最大值。(3) 三相等：求最值时一定要考虑不等式是否能取“=”,否 则会出现错误"一正二定 等”,这三个条件缺一不可.
检测：下面几道题的解答可能有错，如果错了，那么( 1 ) 已 知 函 数 ,求函数的最小值
当且仅当x== 即x=±1 时，函数f(x) 取得最小值2X运用均值不等式的过程中，忽略了“正数”这个条件.
错在哪里?和此时x的取值 .
(2)已知x≥二时，求x²+1的最小值； 2解 ：x²+1≥x √x².1=2x, 当 且 仅 当x²=1 时即x=1 时 ，x²+1 有 最 小 值 2x=2用均值不等式求最值，须满足“定值”这个条件.
所以函数的最小值为4用均值不等式求最值，必须注意“相等”的条件.
(3)求函数y=sinα+的最小值。
如果取等的条件不成立，则不能取到该最值.
4sin a =4sin Q
4 ≥2sin a
sin Q
四 、 课 堂 小 结1.两个重要的不等式(1)a,b ∈R,a²+b²≥2ab, 当且仅当a=b 时等号成立(2)√ab≤ (当且仅当a=b 时等号成立) 2.利用基本不等式求最值已知x,y都是正数，P,S 是常数.(1)xy=P→x+y≥2NP(当且仅当x=y 时，取“=”号).(当且仅当x=y 时，取“=”号).求最值时注意把握“一正，二定，三相等”
练2、求以下问题中的最值( 1 ) 若a>0,则当a=-2 时，4a+= 有最小值12a(2)正数x,y满足x+y=20,xy的最大值100
五，当堂训练练1、下列函数的最小值为2的是 B