甘肃省武威市古浪县土门初级中学2022-2023学年上学期期中九年级教情学情诊断试卷（有答案）

这是一份甘肃省武威市古浪县土门初级中学2022-2023学年上学期期中九年级教情学情诊断试卷（有答案），共12页。试卷主要包含了 选择题，填空题，解答题等内容，欢迎下载使用。
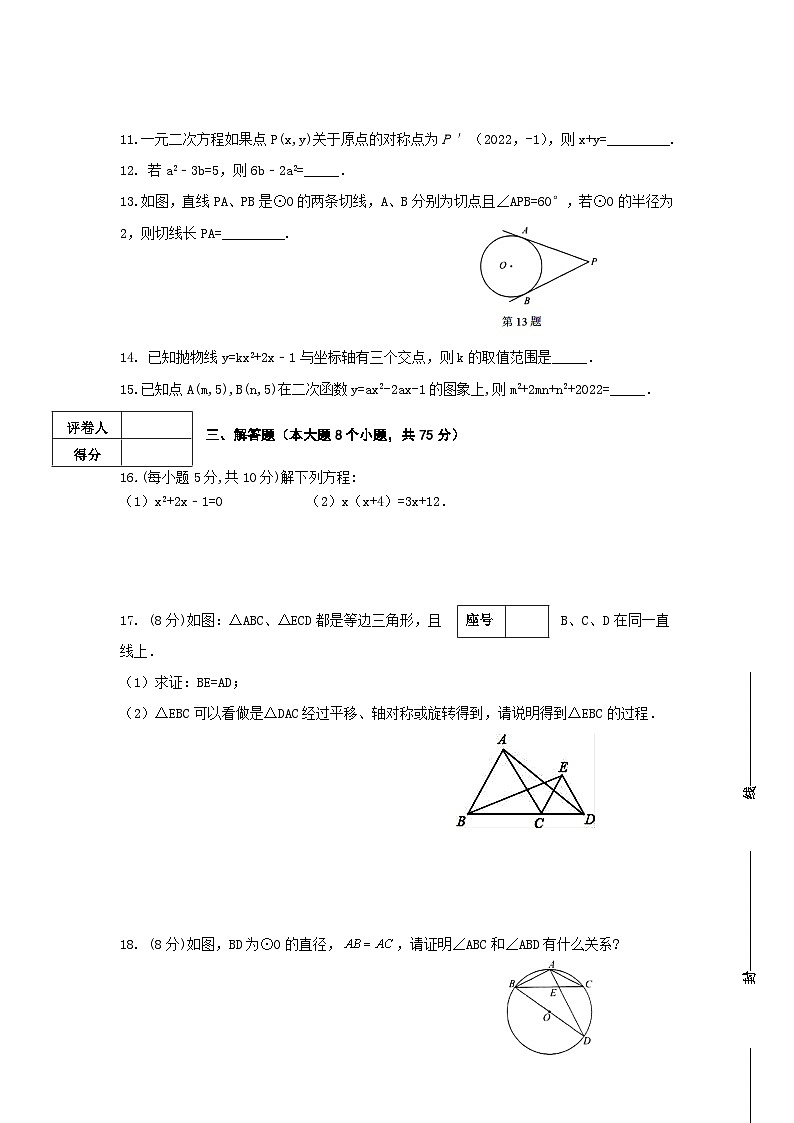
2022-2023学年上学期期中九年级教情学情诊断数 学 注意事项：本试卷共6页，三大题，23个小题，满分120分，考试时间100分钟。请用蓝黑水笔或圆珠笔直接答在试卷上。答题前请将密封线内的项目填写清楚。 题号 一 二三 总分1617181920212223得分            评卷人 得分  一、 选择题（每小题3分，共30分 ） 1.下列图形中，既是轴对称图形又是中心对称图形的是（    ）A.   B.   C.   D. 2. 下列方程中，关于x的一元二次方程是（    ）A.          B.   C. =0             D. 3.一元二次方程配方后可变形为（    ） A.               B.       C.               D. 4.已知x=1是关于x的方程(1-k)x2+k2x-1=0的根,则常数k的值为　(　　)A. 0 B. 1 C. 0或1 D. 0或-15. 把抛物线y=﹣x2向下平移3个单位长度再向左平移2个单位长度的解析式为（　　）A. y=﹣（x+2）2+3             B. y=﹣（x+2）2﹣3C. y=﹣（x+3）2﹣2            D. y=﹣（x﹣3）2+26. 要组织一次排球邀请赛，参赛的每个队之间都要比赛一场，根据场地和时间等条件，赛程计划安排7天，每天安排4场比赛．设比赛组织者应邀请X个队参赛，则x满足的关系式为（　　）A.          B. C. x（x +1）＝28                   D. x（x﹣1）＝287. 若二次函数y=x2+bx+c的图象的对称轴是经过点（2，0）且平行于y轴的直线，且过点（5，5），则关于x的方程x2+bx+c=5的解为（　　）A. x1=0或x2=4              B. x1=1或x2=5                                          C. x1=﹣1或 x2=5                           D. x1=1或x2=﹣58. 已知二次函数y=x2+x+c的图象与x轴的一个交点为（2，0），则它与x轴的另一个交点坐标是 （    ）A. （1，0）     B. （﹣1，0）     C. （2，0）     D. （﹣3，0）9.如图，某小区有一块长为18米，宽为6米的矩形空地，计划在其中修建两块相同的矩形绿地，它们的面积之和为60平方米，两块绿地之间及周边留有宽度相等的人行通道．若设人行道的宽度为x米，则可以列出关于x的方程是(　　)A. x2＋9x－8＝0                  B. x2－9x－8＝0 C. x2－9x＋8＝0                  D. 2x2－9x＋8＝0  （第9题）                      （第10题）10.如图，在平面直角坐标系中，点B、C、E在y轴上，Rt△ABC 经过变换得到Rt△ODE，若点C的坐标为(0，1)，AC=2，则这种变换可以是（    ）A. △ABC绕点C顺时针旋转90°，再向下平移3B. △ABC绕点C顺时针旋转90°，再向下平移1C. △ABC绕点C逆时针旋转90°，再向下平移1D. △ABC绕点C逆时针旋转90°，再向下平移3评卷人 得分   二、填空题（每小题3分，共15分） 11.一元二次方程如果点P(x,y)关于原点的对称点为P ′（2022，-1），则x+y=_________.12. 若a2﹣3b=5，则6b﹣2a2=_____．13.如图，直线PA、PB是⊙O的两条切线，A、B分别为切点且∠APB=60°，若⊙O的半径为2，则切线长PA=_________.   14. 已知抛物线y=kx2+2x﹣1与坐标轴有三个交点，则k的取值范围是_____．15.已知点A(m,5),B(n,5)在二次函数y=ax2-2ax-1的图象上,则m2+2mn+n2+2022=_____．　　　评卷人 得分  三、解答题（本大题8个小题，共75分） 16.(每小题5分,共10分)解下列方程:（1）x2+2x﹣1=0            （2）x（x+4）=3x+12．   座号  17. (8分)如图：△ABC、△ECD都是等边三角形，且B、C、D在同一直线上．（1）求证：BE=AD；（2）△EBC可以看做是△DAC经过平移、轴对称或旋转得到，请说明得到△EBC的过程．    18. (8分)如图，BD为⊙O的直径，，请证明∠ABC和∠ABD有什么关系?     19.(8分) 如图是由边长为1的小正三角形组成的网格图，点O和△ABC的顶点都在正三角形的格点上，将△ABC绕点O逆时针旋转120°得到△A′B′C′．（1）在网格中画出旋转后的△A′B′C′；（2）以O为原点AB所在直线为x轴建立坐标系直接写出A′、B′、C′三点的坐标．       20. (10分)如图，PA为⊙O的切线，A为切点，过A作AB⊥OP，垂足为C，交⊙O于点B，延长BO与PA的延长线交于点D.（1）求证：PB为⊙O的切线；（2）若，，求AB的长.         21.(10分)如图，在Rt△ABC中，∠ACB=90°，点D、E分别在AB、AC上，且，连接CD，将线段CD绕点C按顺时针方向旋转90°后得到CF，连接EF.（1）求证：△BDC≌△EFC；（2）若，，EF//CD，求EF的长.               22. (10分)某数学兴趣小组想借助如图所示的直角墙角∠ADC(两边足够长),用20 m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边).(1)若围成的花园面积为91 m2,求矩形花园AB的长;(2)在点P处有一棵树与墙CD,AD的距离分别为12 m和6 m,要能将这棵树围在花园内(含边界,不考虑树的粗细),又使得花园面积有最大值,求此时矩形花园AB的长.                                               23. (11分)如图，已知二次函数y=ax2+bx+3的图象过点A（﹣1，0），顶点坐标为（1，m）．（1）求该二次函数的关系式和m值；（2）结合图象，解答下列问题：（直接写出答案）①当x取什么值时，该函数的图象在x轴下方？②当﹣1＜x＜2时，直接写出函数y的取值范围．   2022-2023学年上期中九年级数学答案一、选择题．（每小题3分，共30分）1. D  2. A  3.C  4.C  5. B  6. B   7. C  8. D  9.C  10.A二、填空题（每小题3分，共15分）-202112. -1013.14. 且15.2025　【解析】二次函数y=ax2-2ax-1的图象的对称轴是直线x=-=1,∵点A,B的纵坐标相等且都在二次函数的图象上,∴点A,B关于二次函数图象的对称轴对称,∴=1,∴m+n=2,∴m2+2mn+n2+2 022=(m+n)2+2 022=22+2 022=2 026.三、解答题（本大题共75分）16.(每小题5分,共10分)解下列方程:解：（1） 所以 （2） 或 所以 17. （8分）证明：（1）∵△ABC和△ECD都是等边三角形， 即 ... ... ... ... ... ...（3分）在和△BCE中， ≌△BCE.... ... ... ... ... ...（6分）∵△ECD是等边三角形， 同理 以点为旋转中心将逆时针旋转就得到△EBC． ... ... ... ...（8分）18. （8分）答：∠ABC +ABD=90°.证明如下：∵AB=AC∴弧AB=弧AC∴∠ADB=∠ABC ... ... ... ...（4分）又∵BD为⊙O的直径，∴∠BAD=90°∴∠ABD+∠ADB=90°... ... ... ...（6分）又∵∠ADB=∠ABC∴∠ABD+∠ABC=90°... ... ... ...（8分）19. （8分） 解：（1）如图，△A′B′C′即为所求…………………………………5分               （2） 点A′坐标为  点B′坐标为  点C′坐标为 ………………………………………………….3分                                       20. （10分）（1）证明：连接OA，∴由垂径定理可知∠BOC=∠AOC，∵PA是⊙O的切线，∴∠OAP=90°，在△OBP与△OAP中，，∴△OBP≌△OAP（SAS），∴∠OBP=∠OAP=90°，∵OB是⊙O半径，∴PB是⊙O的切线；... ... ... ...（5分）（2）解：∵OB=3，OA=OB，OD=5∴OA=3，DA=4，BD=OB+OD=8，设BP=AP=x，则解得∴BP=6，∴∴S△OPB=BP.OB=OP.BC∴∴又∵AB=2BC，∴... ... ... ...（10分）21. （10分）（1）证明：由旋转的性质，得CD=CF，∠DCF=90°，∴∠DCE+∠ECF=90°，∵∠ACB=90°，∴∠BCD+∠DCE=90°，∴∠BCD=∠ECF，在△BDC和△EFC中，∴△BDC≌△EFC（SAS）；... ... ... ...（5分）（2）解：∵EF//CD，∴∠F+∠DCF=180°，∵∠DCF=90°，∴∠F=90°又∵BC=6，AC=8∴，由得∴CF=4.8又CE=CB=6∴... ... ... ...（10分）22. （10分）解：(1)设AB的长为x m.由题意,得x(20-x)=91, 解得x1=13,x2=7.答:矩形花园AB的长为13 m或7 m. ... ... ... ...（5分） (2)设矩形花园AB的长为a m,面积为s m2.则s=a(20-a)=-a2+20a=-(a-10)2+100.由题意,得解得6≤a≤8.根据二次函数的性质,当6≤a≤8时,s随a的增大而增大,∴当a=8时,s有最大值96.答:此时矩形花园AB的长为8 m. ... ... ... ...（10分）23. （11分）（1）y=﹣x2+2x+3，4；（2）①当x＜﹣1或x＞3时，该函数的图象在x轴下方；②当﹣1＜x＜2时，函数y的取值范围是0＜y≤4解：（1）二次函数的图象过点，顶点坐标为 所以：a-b+3=0解得：   b=2 即二次函数的关系式是 ... ... ... ...（6分）把代入得：  ①∵抛物线开口向下，且经过点 ∴当X＜-1或X＞3时，函数图象在轴下方.②∵抛物线的解析式为：  ∴抛物线的顶点坐标为 ∵抛物线开口向下，∴x=1时，y有最大值，最大值为4.∴当-1＜X＜2时，函数y的取值范围为... ... ... ... ... ... ... ...（11分）