初中数学苏科版八年级上册6.4 用一次函数解决问题课后复习题

这是一份初中数学苏科版八年级上册6.4 用一次函数解决问题课后复习题，共10页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
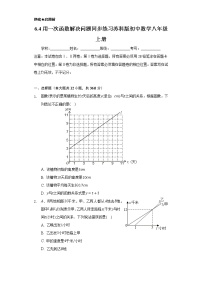
6.4用一次函数解决问题随堂练习-苏科版数学八年级上册学校:___________姓名：___________班级：___________考号：___________ 一、单选题1．下列说法中：①一次函数y＝kx+b，若k＞0，b＜0，那么它的图像过第一、二、三象限；②函数y＝﹣6x是一次函数，且y随着x的增大而减小；③已知一次函数的图像与直线y＝﹣x+1平行，且过点（8，﹣2），那么此一次函数的解析式为y＝﹣x+6；④若一次函数y＝（m﹣6）x+5中，y随x增大而减小，则m的取值范围是m＞6．正确的有（　　）个A．1 B．2 C．3 D．42．在平面直角坐标系中,点A的坐标(-3,2),将点A绕若点O顺时针旋转90°得到点B若正比例函数y=kx的图象经过点B,则k的值为(     )A．6 B．-6 C． D．3．如图，在平面直角坐标系中，点在轴上，在直线上，，若，且、、…、都是等边三角形，从左到右的小三角形（阴影部分）的面积分别记为．则可表示为（    ）  A． B． C． D．4．已知A，B两地相距60km，甲、乙两人沿同一条公路从A地出发到B地，甲骑自行车匀速行驶3h到达，乙骑摩托车．比甲迟1h出发，行至30km处追上甲，停留半小时后继续以原速行驶．他们离开A地的路程y与甲行驶时间x的函数图象如图所示．当乙再次追上甲时距离B地（   ）A．15km B．16km C．44km D．45km5．一个装有进水管和出水管的容器，开始时，先打开进水管注水，3分钟时水量为30升，此时再打开出水管排水，8分钟时水量为20升，此时关闭进水管，直至容器中的水全部排完．在整个过程中，容器中的水量（升）与时间（分钟）之间的函数关系如图所示，则图中容器中的水全部排完图像与轴交点a的值为（   ）A．9 B． C． D．86．某烤鸭店在确定烤鸭的烤制时间时，主要依据的是表中的数据：鸭的质量千克0.511.522.533.54烤制时间分钟406080100120140160180设鸭的质量为x千克，烤制时间为t分钟，估计当x=3.8千克时，t的值约为（    ）A．140 B．160 C．170 D．1807．某星期下午，小强和同学小明相约在某公共汽车站一起乘车回学校，小强从家出发先步行到车站，等小明到了后两人一起乘公共汽车回到学校．图中折线表示小强离开家的路程y（千米）和所用的时间x（分钟）之间的函数关系．下列说法中错误的是（    ）A．小强从家到公共汽车站步行了2千米B．小强在公共汽车站等小明用了10分钟C．公共汽车的平均速度是20千米/小时D．小强乘公共汽车用了20分钟8．如图， 在平面直角坐标系中， 直线与坐标轴交于两点， 于点是线段上的一个动点， 连接， 将线段绕点逆时针旋转， 得到 线段， 连接， 则线段的最小值为（　　）A． B．1 C． D．9．若一次函数的图象不经过第三象限，则下列不等式一定成立的是(    )A． B． C． D．10．关于x的一次函数，下列说法错误的是（    ）A．若函数的图象经过原点，则B．若，则函数的图象经过第一、二、四象限C．函数的图象一定经过点D．当函数的图象经过第一、三、四象限时，m的取值范围是 二、填空题11．小明家和丽丽家相距550米.星期天，小明接到丽丽电话后，两人各自从家同时出发，沿同一条路以各自的速度匀速相向而行，小明出发4分钟后停下休息，等了一会，才与丽丽相遇，然后和丽丽一起返回自己家，返家的速度和丽丽之间的速度相同.若两人距小明家的距离y（米）与他们步行的时间x（分钟）之间的函数关系如上右图所示，结合图象可知，小明中途休息了    分钟.12．如图所示，小明、小白两人分别从A，B两地出发，相向而行，已知小明先出发6分钟后，小白才出发，他们两人相遇后，小白立即以原速返回B地，小明以原速继续向B地前行．小明、小白分别到达B地后停止行走，小明、小白相距的路程y（米）与小明出发的时间x（分钟）之间的关系如图所示，则小白到达B地时，小明与B地相距的路程是     米．13．某航空公司规定，旅客乘机所携带行李的质量x(kg)与其运费y(元)由如图所示的一次函数图象确定，则旅客可携带的免费行李的最大质量为      kg14．如图1，将正方形置于平面直角坐标系中，其中边在轴上，其余各边均与坐标轴平行.直线沿轴的负方向以每秒1个单位的速度平移，在平移的过程中，该直线被正方形的边所截得的线段长为，平移的时间为（秒），与的函数图象如图2所示，则图1中的点的坐标为          ，图2中的值为          .15．已知一次函数图像不经过第一象限，求m的取值范围是          ．16．科学研究发现，空气含氧量y（克/立方米）与海拔高度x（米）之间近似地满足一次函数关系．经测量，在海拔高度为0米的地方，空气含氧量约为299克/立方米；在海拔高度为2100米的地方，空气含氧量约为229克/立方米．已知某山的海拔高度为1200米，该山山顶处的空气含氧量约为      克/立方米．17．若一次函数的图象不经过第四象限，则的取值范围是      ．18．直线经过点和轴负半轴上的一点，如果（为坐标原点）的面积为2，则的值为       ．19．如图，平面直角坐标系中，，，为的中点，是上的一个动点，周长最小时，点的横坐标是      ．20．A、B两地之间的路程为2480米，甲、乙两人分别从A、B两地出发，相向而行，已知甲先出发4分钟后，乙才出发，他们两人在A、B之间的C地相遇，相遇后，甲立即返回A地，乙继续向A地前行甲到达A地时停止行走，乙到达A地时也停止行走，在整个行走过程中，甲、乙两人均保持各自的速度匀速行走，甲、乙两人相距的路程y（米）与甲出发的时间x（分钟）之间的关系如图所示，则乙到达A地时，甲与A地相距的路程是   米． 三、解答题21．为绿化校园，某学校计划购进A、B两种树苗，若购买A树苗10棵，B树苗20棵，需要2300元，若购买A树苗20棵，B树苗10棵，需要2500元，（1）求A、B两种树苗单价各是多少？（2）学校计划购买A、B两种树苗共21棵，且购买B种树苗的数量不超过A种树苗的一半，设购买B种树苗棵，购买两种树苗所需费用为元，请给出一种费用最省的方案，并求出该方案所需费用．22．如图，在平面直角坐标系中，直线与x轴交于点B，与y轴交于点A，，，直线交直线于点C．  (1)求直线的解析式及C点的坐标；(2)如图1，P为直线上一动点且在第一象限内，M、Q为x轴上动点，Q在M右侧且，当时，求最小值；(3)如图2，将沿着射线方向平移，平移后A、O、B三点分别对应D、E、F三点，直线上是否存在N点，使得为等腰直角三角形，若存在，请直接写出N点坐标；若不存在，请说明理由．23．已知一次函数的图象与y轴交点在x轴上方，且y随x的增大而减小，求m的取值范围．24．已知在平面直角坐标系中，A(9,0),直线l：y=.P,Q两点分别同时从O,A出发，P点沿直线l向上运动，Q点沿x轴向左运动，它们的速度相同.连接PQ，当PQ⊥x轴时，P,Q两点同时停止运动.设P点的横坐标为m（m≥0），（1）求m的取值范围；（2）如图1，当△OPQ是以OP为腰的等腰三角形时，求m的值；（3）如果以PQ为边在上方作正方形PQEF,以AQ为边在上方作正方形 QAGH，如图2，①用含m的代数式表示E点的坐标；②当正方形PQEF的某个顶点（Q点除外）落在正方形 QAGH的边上，请直接写出m的值.25．如图，直线分别交x轴、y轴于点A，B，以AB为斜边向左侧作等腰，延长BD交x轴于点C，连接DO，过点D作交y轴于点E．（1）求证：；（2）求OE的长；（3）点P在线段AB上，当PE与的一边平行时，求出所有符合条件的点P的坐标．
参考答案：1．B2．D3．D4．A5．B6．C7．D8．A9．B10．D11．1.512．10013．2014．     （1，0）     5 15．1<m≤216．25917．18．-219．20．300．21．（1）A种树苗单价为90元，B种树苗单价为70元；（2）当A种14棵，B种7棵时所需的费用最省，最小费用为1750元．22．(1)，(2)(3)存在，，或，或，23．24．（1）0≤m≤4；（2）或.（3）①E（9-m，9-）；②m=4, ,.25．（1）略；（2）8；（3）点P的坐标为或．