山东省菏泽市定陶区2022-2023学年八年级下学期期末考试数学试卷(含答案)

这是一份山东省菏泽市定陶区2022-2023学年八年级下学期期末考试数学试卷(含答案)，共10页。试卷主要包含了 函数中自变量取值范围是， 的相反数是，一次函数y＝mx﹣m，已知一次函数的图象过A,B两点，理由如下等内容，欢迎下载使用。
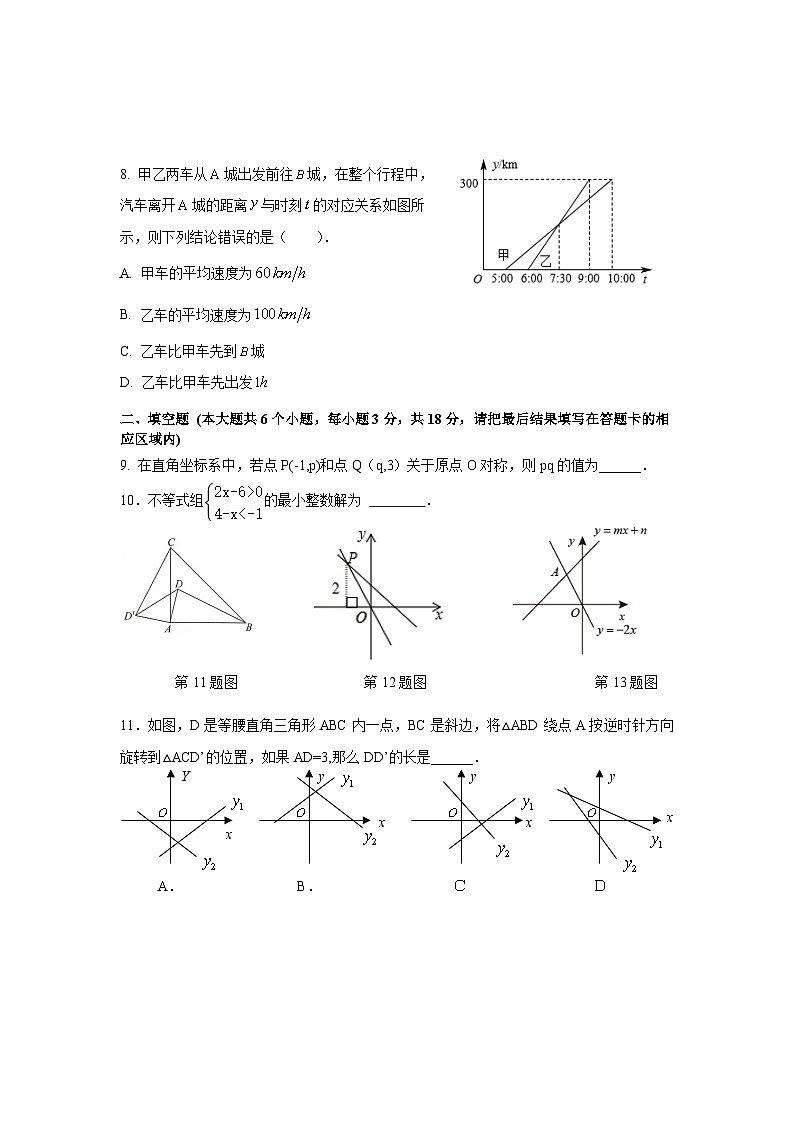
八年级期末数学样题注意事项：1.本试题满分120分,考试时间120分钟   2.请将答案填写在答题卡的相应位置一、选择题(本大题共8个小题，每小题3分，共24分，在每小题给出的四个选项中，只有一个选项是正确的，请把正确的选项涂在答题卡相应位置.)1． 观察下列图形，既是轴对称图形又是中心对称图形的有(   )A. 1个        B. 2个      C. 3个         D. 4个2. 函数中自变量取值范围是（    ）A. 且          B.            C.           D. 且3.        的相反数是（　　）A．﹣3 B．3 C．- D．﹣94．下列属于最简二次根式的是（　　）A． B． C． D．5.一次函数y＝mx﹣m（m为常数且m≠0），若y随x增大而增大，则它的图象经过（　　）A．第一、二、三象限 B．第一、二、四象限 C．第一、三、四象限 D．第二、三、四象限6.如图，在△ABC中，AC=BC，点D、E分别是边AB、AC的中点，将△ABC绕点E旋转180°得△CFE，则四边形ADCF一定是（ ）A. 平行四边形  B. 矩形     C. 菱形  D. 正方形    7. 在同一平面直角坐标系中，一次函数的y1=ax+b与y2=bx+a图象可能是（    ）   8. 甲乙两车从城出发前往城，在整个行程中，汽车离开城的距离与时刻的对应关系如图所示，则下列结论错误的是（    ）．A. 甲车的平均速度为     B. 乙车的平均速度为C. 乙车比甲车先到城          D. 乙车比甲车先出发二、填空题 (本大题共6个小题，每小题3分，共18分，请把最后结果填写在答题卡的相应区域内)9. 在直角坐标系中，若点P(-1,p)和点Q（q,3）关于原点O对称，则pq的值为______．10．不等式组的最小整数解为 　    　．     11．如图，D是等腰直角三角形ABC内一点，BC是斜边，将△ABD绕点A按逆时针方向旋转到△ACD’的位置，如果AD=3,那么DD’的长是______．         12．如图，正比例函数的图象与一次函数y＝﹣x+1的图象相交于点P，点P到x轴的距离是2，则这个正比例函数的解析式是　      　．13.如图，函数y=mx+n与y=-2x的图象交于点A(a,4)，则不等式mx+n＜-2x的解集为_____．14. 三、解答题，一定要细心哟！（本题共78分，请在答题卡上写出必要的计算、推理过程.）15. (4分) 求下列各式的值：（1）                   （2） 16.（6分） 计算：  17. （6分）解不等式组：，并把解集在数轴上表示出来．  （6分）已知直角三角形的两边x、y的长满足求第三边的长.    19.（7分） 已知如图，AD、BF相交于点O，点E、C在BF上，BE=FC，AC=DE，AB=DF，（1）求证：△ABC≌△DFE；(2)连接BD、FA，求证：四边形ABDF是平行四边形．     20.（7分）已知一次函数的图象过A(-3,-5),B(1,3)两点.（1）求这个一次函数的表达式；（2）判断点P（-2,1）是否在这个一次函数的图象上.   21.（8分）如图，在正方形网格中，每个小正方形的边长均为个单位长度，△ABC的三个顶点和点D均在格点上．（1）若将△ABC平移，使点A的对应点为点D，点B，C的对应点分别为点E，F．请画出平移后的△DEF；连接AD，CF，则这两条线段之间存在什么关系？请直接写出结论；（2）将△ABC绕点D顺时针旋转90°得到△A1B1C1，若点D是坐标原点，点A的坐标为(-6,2)．请画出△A1B1C1，并写出点A的对应点A1的坐标．       22．（10分）如图，已知函数y＝x+1和y＝ax+3的图象交于点P，点P的横坐标为1，（1）关于x，y的方程组的解是　                　；（2）a＝　                　；（3）求出函数y＝x+1和y＝ax+3的图象与x轴围成的几何图形的面积．   23.(12分)在抗击新冠肺炎疫情期间,某单位给某乡中小学捐献一批饮用水和蔬菜共320件，其中饮用水比蔬菜多80件.(1) 求饮用水和蔬菜各有多少件?(2) 现计划租用甲、乙两种货车共8辆，一次性将这批饮用水和蔬菜全部运往该乡中小学.已知每辆甲种货车最多可装饮用水40件和蔬菜 10件，每辆乙种货车最多可装饮用水和蔬 菜各20件. 则运输部门安排甲、乙两种货车时有几种方案? 请你帮助设计出来;(3) 在(2)的条件下，如果甲种货车每辆需付运费 400元，乙种货车每辆需付运费360元运 输部门应选择哪种方案可使运费最少? 最少运 费是多少元?           24.(12分) (1) 如图①，已知正方形ABCD，点E，F分别在边BC 、AB上，且BE=BF. 此时AF与CE有怎样的数量关系?(2) 如图②，ΔBEF绕点B顺时针旋转∠a，当0°< a <90°时，连接AF、CE，此时AF与CE仍有(1)中的数量关系吗? 如果成立，请说明理由. 否则，请举出反例;(3)当a=90°时(图③)，连接AF、CE，猜想AB与BE有什么数量关系时，直线AF是EC的垂直平分线? 试说明理由.      八年级期末数学参考答案一、选择题：1．C  2．D  3．A  4．C  5．C    6．  B  7．C  8．D  二、填空题：9．-3   10．x=6   11．  12．y= -2x   13．x＜ -2     14．-2a       三、解答题15．解：（1）……………………………… 2分（2）………………………………2分 16.．解：（1）……………………………………………3分（2）   ……………………………………………3分17．解：解不等式①，得： ，……………………………………2分        解不等式②，得： ，…………………………………4分则不等式组的解集为-4＜x≤1   ………………………………5分解集在数轴上表示如图：…………………6分  解：               ……………………… 2分                    ………………………3分                        ………………………4分………………………5分………………………6分19证明：(1)∵BE=CF∴BE+CE=CF+CE即 BC=EF      ………………………………1分在△ABC和△DFE中，    ……………………………3分∴△ABC≌△DFE（SSS） ………………………4分  (2)∵△ABC≌△DFE∴∠ABF=∠DFE,………………………………5分∴AB∥DF………………………………6分又∵AB=DF∴四边形ABDF是平行四边.形.………………………………7分 20.解：(1)  设这个一次函数的表达式为： ……………………………………1分          将A(-3，5)，B(1，3)代入，得：                                  ……………………………………3分解得                                  …………………………………4分          ………………………5分（2）                 ………………………………6分∴点P(-2，1)不在这个一次函数的图象上.                 ………………………7分 21.（1）如图，△DEF即为所作；                               ……AD∥CF ,                                ………………………………3分 AD=CF;                                 ………………………………4分 （2）                       ………………………………6分     点A1的坐标为（2,  6）                               …………………8分                    22.（1）      ………………………………2分 （2）  -1       ………………………………4分    （3）∵函数y=x+1与x轴交于点A（-1,  0）     ……………5分函数y=-x+3与x轴交于点B（3,  0）     ……………6分∴AB=3-(-1)=4                          ……………7分又∵P(1, 2) ∴点P到x轴的距离为2                ……………8分∴S△PAB=                    ……………10分23.解：(1) （方法不唯一）设饮用水为x件，则蔬菜为（x-80）件，     ……………1分  根据题意，得 x+x-80=320                              ……………2分            解，得  x=200          经检验方程的解符合题意. 此时x-80=120.                          答：饮用水为200件，则蔬菜为120件       ……………3分（2）设租用甲种货车m辆，则租用乙种货车（8-m）辆， …………4分根据题意，得                        ……………6分解得                                 ……………7分∵m为正整数∴m=2或3或4                                 ……………8分                   故安排甲、乙两种货车有种方案：①  甲车2辆，乙车6辆；②  甲车3辆，乙车5辆；③  甲车4辆，乙车4辆；                      ……………9分（3）3种方案的运费分别为：① 2×400+6×300=2960（元）；② 3×400+5×300=3000（元）；③ 4×400+4×300=3040（元）；所以方案① 运费最少，最少运费是2960元.         ……………12分 24.(1)AF与CE的数量关系是AF=CE, 理由如下：              ……………1分   ∵四边形ABCD是正方形∴AB=BC                                                ……………2分 ∵BE=BF∴AB-BF=BC-BE                         即AF=CE                                                  ……………3分 （2）仍有AF=CE成立 理由如下：       ……………………4分  ∵四边形ABCD是正方形∴AB=BC ，∠ABC=∠EBF=90°         ……………………5分∴∠ABC-∠FBC=∠EBF-∠FBC即∠ABF=∠CBE                    ……………………6分在△ABF和△CBE中，    ∴△ABF≌△CBE（SAS）            ……………………7分∴AF=CE                           ……………………8分 (3).理由如下：……………………9分如图③所示，连接AC，当ɑ=90°时，点F落在BC边上，∵∠ABC=∠FBE=90°∴A、B、E三点共线                             ∵直线AF是CE的垂直平分线                       ∴AE=AC                                       ……………………10分∵四边形ABCD是正方形                                ……………………11分                             ……………………12分