第4章 一次函数复习 北师大版八年级上册数学课件

这是一份第4章 一次函数复习 北师大版八年级上册数学课件，共25页。

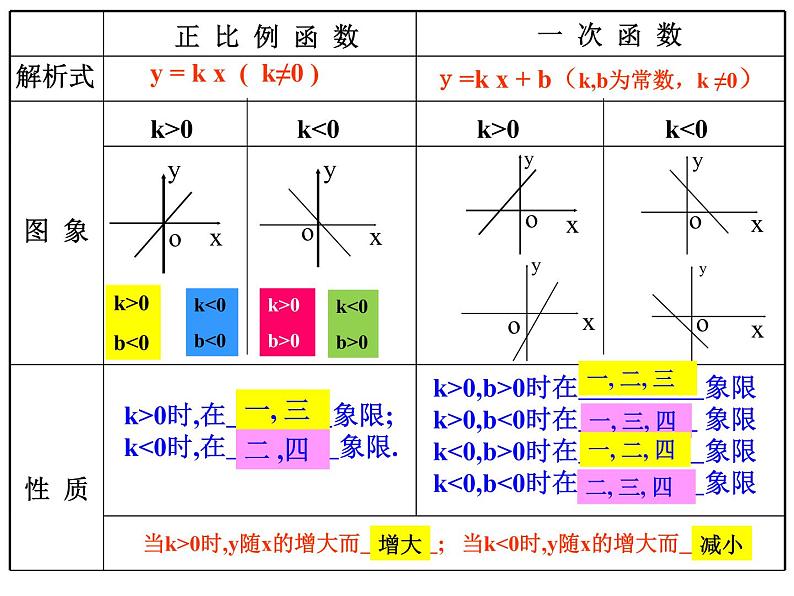
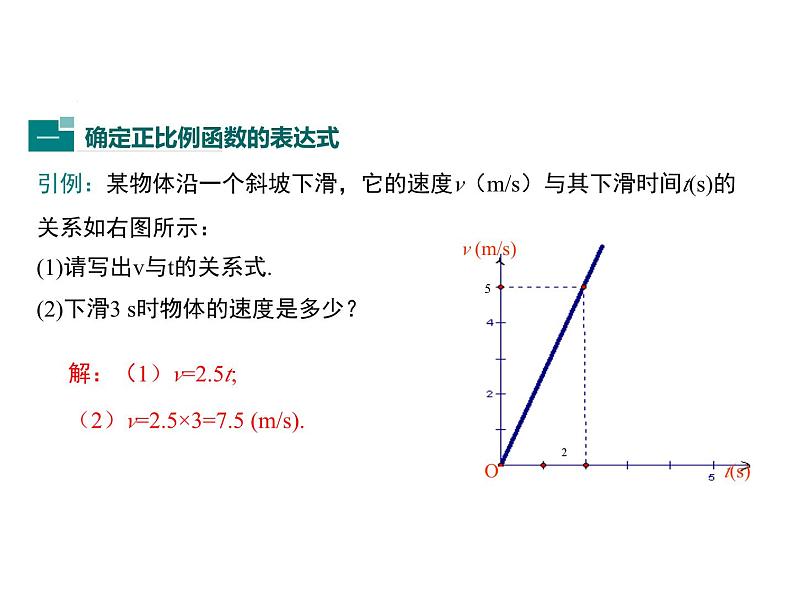
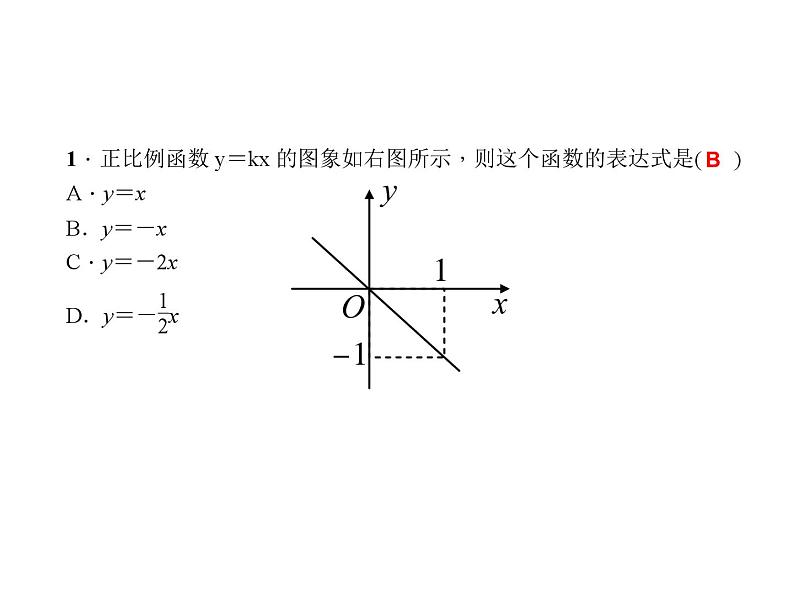
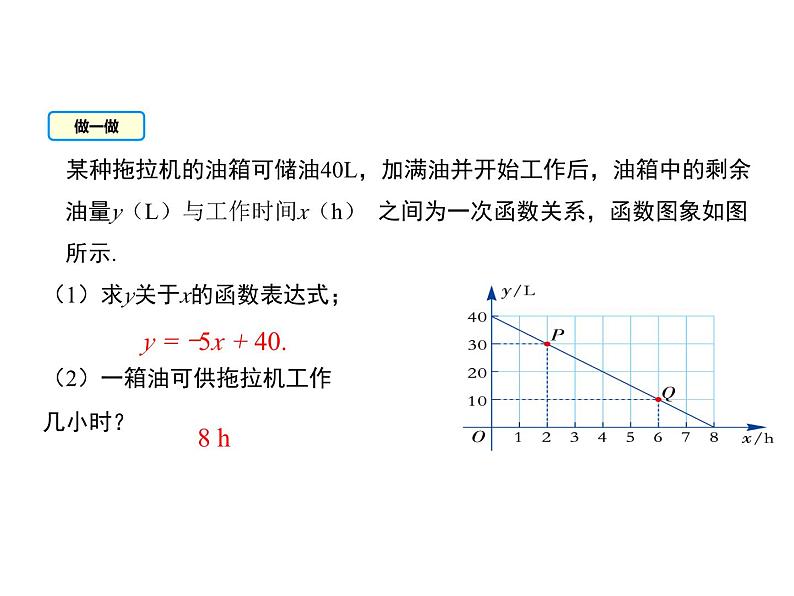
3、一次函数y=kx+b(k≠0)的图象是过点（0，__),（____，0)的一条直线。★概念中要注意： ⑴x的次数是___次。 ⑵x的系数_____。一、知识要点：1、一次函数的概念： 一般地，如果y= (k，b是常数，k≠0)，那么y叫做x的一次函数. 特别地，当______时，一次函数y＝kx＋b变为 y＝kx(k是常数，k≠0)，这时y叫做x的正比例函数．1k≠02、正比例函数y=kx(k≠0)的图象是过点（0， ），(1，__)的一条直线。0kbb＝0 4、一次函数y=kx+b(k ≠ 0)与正比例函数y=kx(k≠0)的性质：kx ＋b 一 次 函 数正 比 例 函 数解析式 图 象性 质 y = k x ( k≠0 ) k<0 k>0b>0k>0b<0k<0b>0k<0b<0k>0时,在 象限;k<0时,在 象限.k>0,b>0时在 象限k>0,b<0时在 象限k<0,b>0时在 象限k<0,b<0时在 象限当k>0时,y随x的增大而 ; 当k<0时,y随x的增大而 . k>0　 k<0 k>0　 ｙ=k x + b（k,b为常数，k ≠0）一, 三二 ,四一, 二, 三一, 三, 四一, 二, 四二, 三, 四增大减小引例：某物体沿一个斜坡下滑，它的速度v（m/s）与其下滑时间t(s)的关系如右图所示： (1)请写出v与t的关系式.(2)下滑3 s时物体的速度是多少？v (m/s)t(s)O解：（1）v=2.5t;（2）v=2.5×3=7.5 (m/s).52B 例2：已知一次函数的图象经过(0，5)、(2，－5)两点，求一次函数的表达式．解：设一次函数的表达式为y＝kx＋b，根据题意得，∴－5＝2k＋b，5＝b，解得b＝5，k＝－5.∴一次函数的表达式为y＝－5x＋5.解：设直线l为y=kx+b,　　∵l与直线y=-2x平行，∴k= -2. 又∵直线过点（0，2）， ∴2=-2×0+b, ∴b=2, ∴直线l的表达式为y=-2x+2.已知直线l与直线y=-2x平行，且与y轴交于点(0，2)，求直线l的表达式.练一练做一做 某种拖拉机的油箱可储油40L，加满油并开始工作后，油箱中的剩余油量y（L）与工作时间x（h） 之间为一次函数关系，函数图象如图所示.（1）求y关于x的函数表达式；（2）一箱油可供拖拉机工作几小时？ y = -5x + 40.8 h 根据图象确定一次函数的表达式的方法：从图象上选取两个已知点的坐标，然后运用待定系数法将两点的横、纵坐标代入所设表达式中求出待定系数，从而求出函数的表达式．归纳总结三、归纳小结1.设—— 一次函数表达式 y=kx+b或者y=kx；2.代—— 将点的坐标代入y=kx+b中,列出关于k、b 的方程;3.解—— 解方程求出k、 b 值；4.定—— 把求出的k、b值代回到表达式中即可.怎样求一次函数的表达式？这种求函数解析式的方法叫做待定系数法例4、已知一次函数的图象如图：求该一次函数的解析式；二、典型例题：1．如图，一次函数的图象过点A，且与正比例函数y＝－x的图象交于点B，则该一次函数的表达式为( )A．y＝－x＋2 B．y＝x＋2C．y＝x－2 D．y＝－xB2．如图，一次函数y＝kx＋2的图象经过A(2，4)，与x轴交于点C，求△AOC的面积．3．某图书馆开展两种方式的租书业务：一种是使用会员卡，另一种是使用租书卡，使用这两种卡租书，租书金额y(元)与租书时间x(天)之间的关系如下图所示：(1)分别写出用租书卡和会员卡租书金额y(元)与租书时间x(天)之间的关系式；(2)两种租书方式每天的收费是多少元？(x<10)解：(1)设使用会员卡租书金额y1(元)与租书时间x(天)之间的关系式为y1＝kx＋b.从图象可知它过(0，20)，可得b＝20，将(10，50)，代入关系式得k＝3.∴y1＝3x＋20.设使用租书卡租书金额y2(元)与租书时间x(天)之间的关系式为y2＝mx.它经过(10，50)，代入得10m＝50，m＝5.∴y2＝5x　(2)会员卡方式每天收费(50－20)÷10＝3(元)，租书卡方式每天收费5元4．某省由于持续高温和连日无雨，水库蓄水量普遍下降，如图所示是某水库蓄水量V(万立方米)与干旱时间t(天)之间的关系图．请你根据此图填空：(1)水库原蓄水量是________万立方米，干旱持续10天，蓄水量为_______万立方米；(2)若水库的蓄水量小于400万立方米时，将发出严重干旱预报，则持续干旱_______天后，将发出严重干旱预报．按此规律，持续干旱_______天时，水库的水将干涸．10008003050知识点二：从一次函数图象中获取信息5．早晨，小张去公园晨练，如图是他离家的距离y(千米)与时间t(分钟)的函数图象，根据图象信息，下列说法正确的是( )A．小张去时所用的时间多于回家所用的时间B．小张在公园锻炼了20分钟C．小张去时的速度大于回家的速度D．小张去时走上坡路，回家时走下坡路C6．李老师开车从甲地到相距240千米的乙地，如果油箱剩余油量y(升)与行驶里程x(千米)之间是一次函数关系，其图象如图所示，那么到达乙地时油箱剩余油量是______升．27．如图，汽车由天津驶往相距120 km的北京，s(km)表示汽车离开天津的距离，t(h)表示汽车行驶的时间．(1)汽车行驶______h可从天津到北京，速度是___________；(2)当汽车行驶了1 h，离开天津_______km.430 km/h308．某种摩托车油箱最多可储油10升，加满油后，油箱中剩余量y(升)与摩托车行驶路程x(千米)之间关系如图所示，据图象回答：(1)一箱汽油可供摩托车行驶多少千米？(2)摩托车每行驶100千米消耗多少升汽油？(3)油箱中剩余量小于1升时摩托车将自动报警，行驶多少千米后，摩托车将自动报警？解：(1)由题可得y＝－0.02x＋10，当y＝0，则0＝－0.02x＋10，解得x＝500，∴一箱汽油可供摩托车行驶500千米　(2)10÷(500÷100)＝2(升)，摩托车每行驶100千米消耗2升汽油(3)当y＝1时，1＝－0.02x＋10，解得x＝450，当摩托车行驶了450千米后将自动报警9．(2017·泸州模拟)五一节期间，王老师一家自驾游去了离家170千米的某地，如图是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象，当他们离目的地还有20千米时，汽车一共行驶的时间是( )A．2小时 B．2.2小时C．2.25小时 D．2.4小时C5.一次函数y=ax+b与y=ax+c(a>0)在同一坐标系中的图象可能是（　 　）4.已知一次函数y=kx+b,y随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是( 　) 　(A) 　　　　 　(B) 　（C） 　　（D）AA三、练一练 6.如图，一次函数y=kx+b的图象与正比例函数y=2x的图象平行且经过点A(1,﹣2)，求k与b的值。 三、练一练解：∵直线y=kx+b与直线y=2x平行∴直线为y =2x - 4∴k= 2又直线过点A(1,-2) ∴-２＝２×1+b∴b= -41．一次函数y＝－x＋2的图象不经过的象限是(　　) A．第一象限 B．第二象限 C．第三象限 D．第四象限2．直线y＝2x－4与y轴的交点坐标是(　　) A．(4，0) B．(0，4) C．(－4，0) D．(0，－4)3.关于直线m：y＝kx＋k(k≠0)，下列说法不正确的是(　　) A．点(0，k)在m上 B．m经过定点(－1，0) C．当k＞0时，y随x的增大而增大 D．m经过第一、二、三象限4．将函数y＝－3x的图象沿y轴向上平移2个单位长度后，所得图象对应的函数关系式为(　　) A．y＝－3x＋2 B．y＝－3x－2 C．y＝－3(x＋2) D．y＝－3(x－2) 5．已知点(－1，y1)，(4，y2)在一次函数y＝3x－2的图象上，则y1，y2，0的大小关系是(　　)A．00时，x的取值范围是(　　)A．x＜0 B．x＞0 C．x＞－2 D．x＜－27．在同一平面直角坐标系中，直线y＝4x＋1与直线y＝－x＋b的交点不可能在(　　)A．第一象限 B．第二象限 C．第三象限 D．第四象限8．函数y1＝－2x和y2＝ax＋3的图象相交于点A(m，2)，则关于x的不等式－2x＞ax＋3的解集是(　　)A．x＞2 B．x＜2C．x＞－1 D．x＜－1