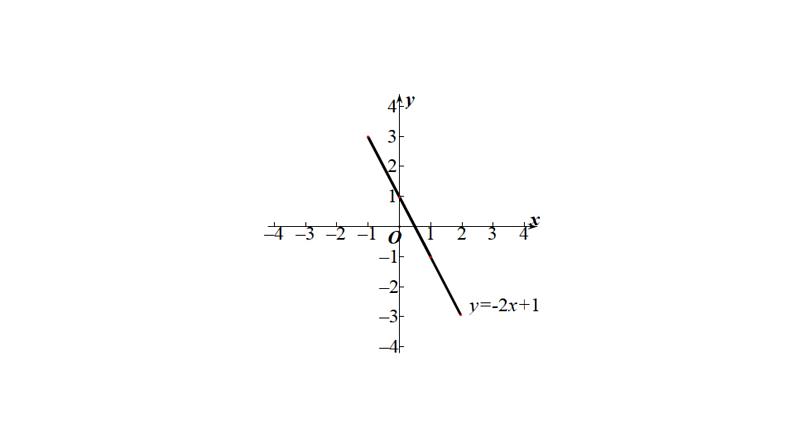
北师大版八年级上册4 一次函数的应用教学课件ppt

这是一份北师大版八年级上册4 一次函数的应用教学课件ppt，共24页。PPT课件主要包含了学习目标，复习导入，探究新知，解列表，典例精讲，课堂练习，课堂小结等内容，欢迎下载使用。

1．经历一次函数图象的画图过程，初步了解画函数图象的一般步骤；经历一次函数图象变化情况的探索过程，发展数形结合的意识和能力。2．能熟练画出一次函数的图象；掌握一次函数及其图象的简单性质。
1．什么叫函数?在某个变化过程中，有两个变量x和y，如果给定一个x值，相应地就确定一个y值，那么我们称y是x的函数，其中x是自变量，y是因变量．2．函数的表示方法有哪几种?（1）解析法；（2）列表法；（3）图象法．3．上节课我们学习了正比例函数的图象，请画出正比例函数y=－2x的图象。
要回答这个问题，必须弄清楚以下几点：（1）函数的图象是由无数个点构成的．（2）这些点在坐标系中是一对一对的有序实数．（3）此解析式实际上是一个二元一次方程，它的一对一对的x、y值可看作是图象上的点的坐标．
（4）要找出它的某个点，实际上就是求出这个二元一次方程的一组解．（5）把x的值作为横坐标，y的值作为纵坐标．（6）把函数作图问题转化为求方程的解的问题 ．
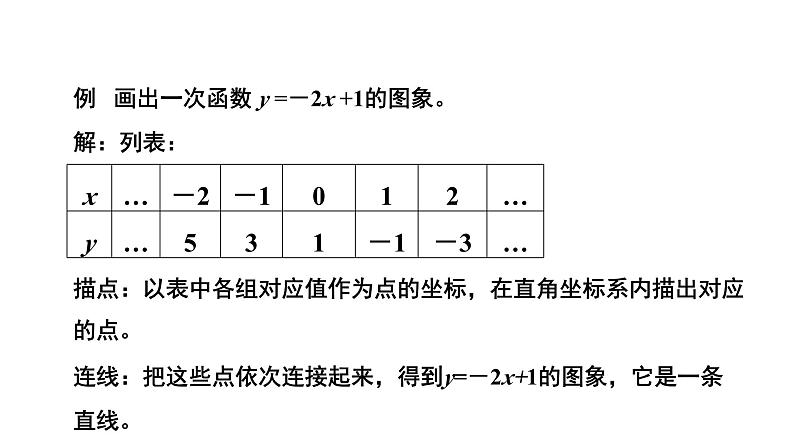
例 画出一次函数 y =－2x +1的图象。
描点：以表中各组对应值作为点的坐标，在直角坐标系内描出对应的点。
连线：把这些点依次连接起来，得到y=－2x+1的图象，它是一条直线。
议一议：问题1：一次函数y=－2x+1图象是什么形状呢？问题2：凡是满足关系式y =－2x+1的x，y的值所对应的点(x，y)，如(1，－1)，(4，－7)…．都在一次函数y=－2x+1的图象上吗？问题3：请你从一次函数y =－2x+1的图像上任意取一点，检验该点的横坐标x和纵坐标y是否满足关系式y =－2x+1．
问题4：一次函数y=kx+b(k≠0)的图像都是一条直线吗？举例验证．问题5：几个点可以确定一条直线？问题6：画一次函数图像时，只要取几个点？
画一次函数图象，只过两个点画直线就行．
问题7：你认为一次函数y=kx+b的图象是什么形状?有什么特点？你是怎样理解的？
画出一次函数图象的关键是选取适当的两点，然后连线即可．为了描点方便，对于一次函数y=kx+b(k，b是常数，k≠0)通常选取(0，b)与(－ ，0)两点．
1．一次函数y=kx+b的图象的特点：一次函数y=kx+b的图象是一条直线作一次函数y=kx+b的图象只要确定两个点，再过这两个点作直线就可以了．一次函数y=kx+b的图象也称为直线y=kx+b。
2．作函数图象的一般步骤：列表：列出自变量和函数的对应值描点：根据上表的对应值描出点的位置连线：根据描出点的发展趋势，用光滑的线把点连接起来．
做一做 ：在同一直角坐标系内分别画出一次函数y=2x+3，y=－x，y=－x+3和y=5x－2的图象
议一议（1）上述四个函数中，随着x值的增大，y的值分别如何变化？相应图象上点的变化趋势如何？（2）直线y =－x与y =－x+3的位置关系如何？你能通过适当的移动将直线y =－x变为直线y =－x+3吗？一般地，直线 y =kx+b与y=kx+5又有怎样的位置关系呢？（3）直线y =2x+3与y =－x+3有什么共同点？一般地，你能从函数y=kx+b的图象上直接看出b的数值吗？
问题：对于直线y=kx+b(k，b是常数，k≠0)，常数k和b的取值对于直线的位置各有什么影响？说说你的看法．
当k值相同，且b值也相同时，两个函数图象又是什么样的位置关系?
小结：一次函数y=kx+b的图象经过点（0，b）。
两个一次函数k相等时，图象互相平行；两个一次函数b相等时，过同一点（0，b）。
当k>0时，y值随x值的增大而增大；当k<0时，y值随x值的增大而减小。
正比例函数或一次函数(y=kx+b)的图象如图所示，请确定k、b的情况：
解：（1）由图可以看出，k=1，b=0．（2）由图可以看出，k=－1，b=0．（3）由图可以看出，k=－1，b=1．（4）由图可以看出，k=－1，b=－1．
1．下列函数中，y的值随x值的增大而增大的函数是 ( )A．y=－2x B．y=－2x+1C．y=x－2 D．y=－x－22．若一次函数y=kx+b中，y随x的增大而减小，则（ ）A．k＜0，b＜0 B．k＜0，b＞0C．k＜0，b≠0 D．k＜0，b为任意数
3．若直线y=kx+b经过A（1，0），B（0，1），则（ ）A．k=－1，b=－1 B．k=1，b=1C．k=1，b=－1 D．k=－1，b=14．一次函数y=5kx－5k－3，当k=______时，图象过原点；当k______时，y随x的增大而增大5．直线y=3－9x与x轴的交点坐标为______，与y轴的交点坐标为______．
6 ．（1）对于函数y＝5x＋6，y的值随x值的减小而______ ；（2）对于函数 ，y的值随x值的______而增大．
7 ．对于一次函数y＝（2－m）x＋1 ．（1）若y的值随x值的增大而增大，则m的取值范围是什么？（2）若y的值随x值的增大而减小，则m的取值范围是什么？
解：（1）由题意得2－m＞0，所以m＜2．（2）由题意得2－m＜0，所以m＞2 ．
这节课的收获有哪些?1．一次函数图象是直线，所以可以说直线y=kx+b(k≠0) ．会用“两点法”画一次函数的图象．2．学习一次函数，既离不开数，也离不开图形．3．当k值相同，b值不同时，两个一次函数图象平行，当k值不同时，两个一次函数图象相交．
4．一条直线通过平移可以得到另一条直线，函数关系式中k，b值的变化情况．5．一次函数y=kx+b（k≠0) ，当k>0时，y值随x值的增大而增大；k<0时，y值随x值的增大而减小．6．一条直线通过平移可以得到另一条k值相等直线