初中人教版28.1 锐角三角函数教学课件ppt

这是一份初中人教版28.1 锐角三角函数教学课件ppt，共17页。PPT课件主要包含了教学目标，教学重难点，教学设计，教材P62探究．，固定值，对边与斜边的比，活动4例题与练习，活动5，正弦的定义及运用等内容，欢迎下载使用。
1．理解锐角正弦的概念，能够运用sin A表示直角三角形两边的比值及进行简单的计算．2．体会数形结合思想在解决数学问题中的广泛应用．
理解锐角正弦sin A的意义，能用它进行简单的计算．
活动1 新课导入
为了绿化荒山，某地打算从位于山脚下的机井房沿着山坡铺设水管，在山坡上建一座扬水站，对坡面绿地进行喷灌.先测得斜坡的坡脚（∠A）为30°，为使出水口的高度为35m,需要准备多长的水管？
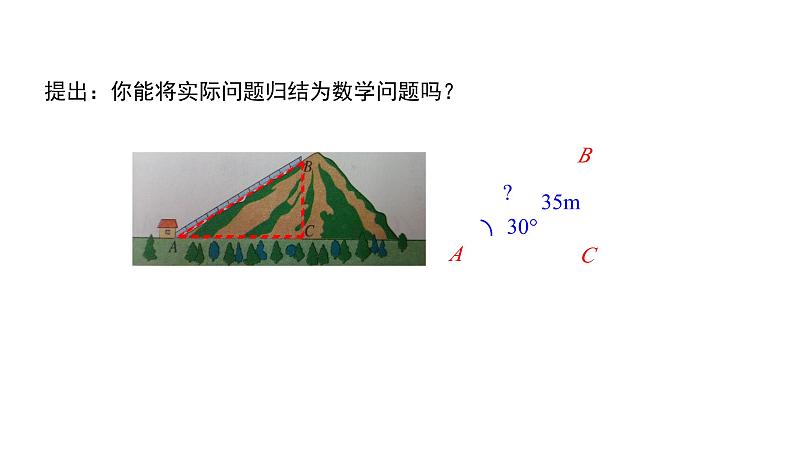
提出：你能将实际问题归结为数学问题吗？
如图，在Rt△ABC中，∠C=90°，∠A=30°，BC=35m,求AB.
活动2 探究新知
1．教材P61问题．提出问题：(1)问题中是根据什么求出水管长度的？(2)如果出水口的高度是40 m时，需要准备多长的水管？(3)如果出水口的高度是a m时，需要准备多长的水管？你从中发现了什么规律？(4)教材P61第1个思考，由此你能得出什么结论？
2．教材P61第2个思考．提出问题：(1)已知条件是什么？要求的是什么？我们可以根据什么定理来求解？根据勾股定理，你列出的等式是什么？ 的值与三角形的大小有关系吗？由此，你能得出什么结论？(2)在上面求AB(所需水管的长度)和∠A的对边与斜边的比 的过程中，你能得出什么结论？可以相互交流．(3)当∠A是任意一个确定的锐角时，它的对边与斜边的比是否也是一个固定值呢？
活动3 知识归纳
1．在Rt△ABC中，当锐角A的度数一定时，无论这个直角三角形大小如何，∠A的对边与斜边的比都是一个________．
2．如图，在Rt△ABC中，∠C＝90°，我们把锐角A的______________叫做∠A的正弦，记作sin A，即sin A＝____．
如图，在Rt△ABC中，∠C=90°，求sinA 和sinB的值.
解析：求sinA 和sinB的值，实质就是求∠A与∠B的对边与斜边的比.
例1　教材P63例1.
解：如图(1),在Rt△ABC中，由勾股定理得
如图(2),在Rt△ABC中，由勾股定理得
例2　如图，在矩形ABCD中，DE⊥AC于点E.设∠ADE＝α且sin α＝ ，AB＝4，求AD的长．
解：∵∠ADE＋∠DAC＝90°，∠DAC＋∠BAC＝90°， ∴∠ADE＝∠BAC，
设AC＝5x，BC＝4x，则AB＝3x＝4，
例3　如图，⊙O是△ABC的外接圆，AD是⊙O的直径．若⊙O的半径为 ，AC＝2，求sin B的值．
解：连接CD.∵AD是⊙O的直径，∴∠ACD＝90°，
由圆周角定理，得∠B＝∠D，
1．教材P64练习第1题．
2．如图，在⊙O中过直径AB延长线上的点C作⊙O的一条切线，切点为D.若AC＝7，AB＝4，则sin C的值为_____．
3．如图，把含30°角的三角尺ABC绕点B按逆时针方向旋转90°到三角尺DBE的位置，连接AD，求sin ∠ADE的值．
解：过点E作EF⊥AD于点F.设BD＝x.由旋转的性质，得∠ABD＝90°，AB＝BD＝x，∠EDB＝30°，∴∠DAB＝45°，AD＝x.
∵∠AFE＝90°，∠DAB＝45°，∴△AEF是等腰直角三角形，
完成《名师测控》随堂反馈手册《精英新课堂》变式训练手册
活动6 课堂小结