江西省南昌市雷式学校2023-2024学年九年级上学期月考数学试题(无答案)

南昌市雷式学校2023－2024上学期10月份大练习

九年级数学试卷

一、单选题（每题3分，共18分）

1．抛物线y＝3x2向右平移1个单位，再向下平移2个单位，所得到的抛物线是（    ）

A．y＝3（x－1）2－2 B．y＝3（x＋1）2－2 C．y＝3（x＋1）2＋2 D．y＝3（x－1）2＋2

2．下列图形中，是中心对称图形的是（    ）

A．B．C．D．

3．下列说法正确的是（    ）

A．平分弦的直径垂直于弦 B．三角形的外心到这个三角形的三边距离相等

C．相等的圆心角所对的弧相等 D．等弧所对的圆心角相等

4．已知二次函数的图象如图所示，给出下列结论：①abc<0；②4a－2b＋c>0；③a－b>m（am＋b）（m为任意实数）；④；其中正确的结论有（    ）

A．1个 B．2个 C．3个 D．4个

5．关于x的一元二次方程根的情况，下列判断正确的是（    ）

A．因为m可以取不同实数，因此方程可能有两个不相等的实数根，或两个相等的实数根，也可能无实数根

B．当时，方程变为，而有两个不相等实数根，因此有两个不相等的实数根

C．方程总有两个实数根

D．当时，方程变为，而有两个相等实数根，因此有两个相等的实数根

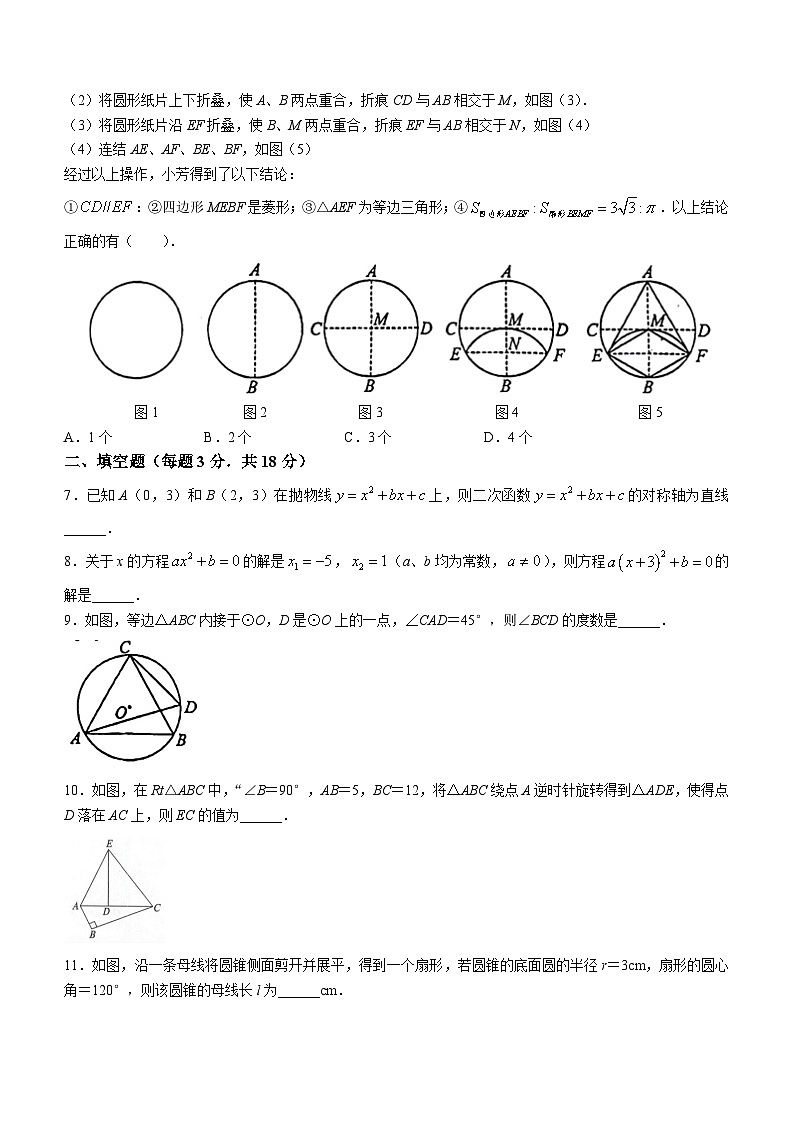
6．一张圆形纸片，小芳进行了如下连续操作：

（1）将圆形纸片左右对折，折痕为AB，如图（2）

（2）将圆形纸片上下折叠，使A、B两点重合，折痕CD与AB相交于M，如图（3）．

（3）将圆形纸片沿EF折叠，使B、M两点重合，折痕EF与AB相交于N，如图（4）

（4）连结AE、AF、BE、BF，如图（5）

经过以上操作，小芳得到了以下结论：

①：②四边形MEBF是菱形；③△AEF为等边三角形；④．以上结论正确的有（    ）．

图1            图2             图3                图4                 图5

A．1个 B．2个 C．3个 D．4个

二、填空题（每题3分．共18分）

7．已知A（0，3）和B（2，3）在抛物线上，则二次函数的对称轴为直线______．

8．关于x的方程的解是，（a、b均为常数，），则方程的解是______．

9．如图，等边△ABC内接于⊙O，D是⊙O上的一点，∠CAD＝45°，则∠BCD的度数是______．

10．如图，在Rt△ABC中，“∠B＝90°，AB＝5，BC＝12，将△ABC绕点A逆时针旋转得到△ADE，使得点D落在AC上，则EC的值为______．

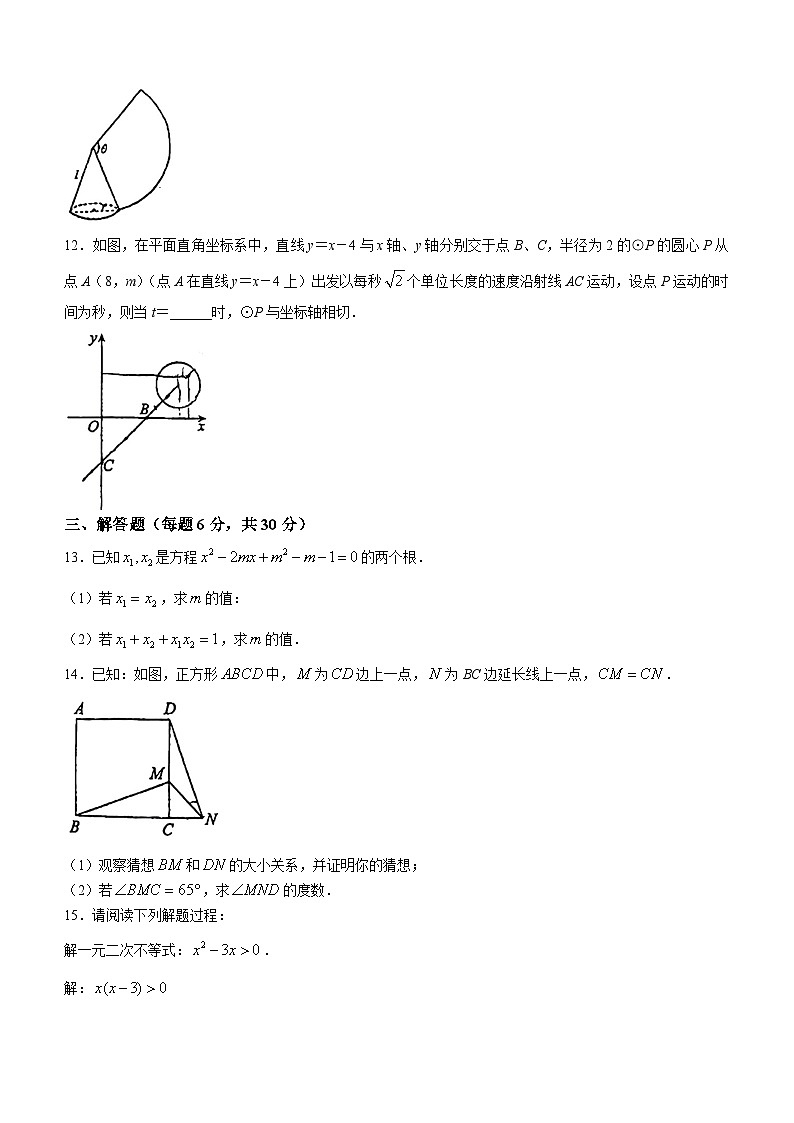
11．如图，沿一条母线将圆锥侧面剪开并展平，得到一个扇形，若圆锥的底面圆的半径r＝3cm，扇形的圆心角＝120°，则该圆锥的母线长l为______cm．

12．如图，在平面直角坐标系中，直线y＝x－4与x轴、y轴分别交于点B、C，半径为2的⊙P的圆心P从点A（8，m）（点A在直线y＝x－4上）出发以每秒个单位长度的速度沿射线AC运动，设点P运动的时间为秒，则当t＝______时，⊙P与坐标轴相切．

三、解答题（每题6分，共30分）

13．已知是方程的两个根．

（1）若，求的值：

（2）若，求的值．

14．已知：如图，正方形中，为边上一点，为BC边延长线上一点，．

（1）观察猜想和的大小关系，并证明你的猜想；

（2）若，求的度数．

15．请阅读下列解题过程：

解一元二次不等式：．

解：

∴，或，解得或．

∴一元二次不等式的解集为或．

结合上述解答过程回答下列问题：

（1）上述解题过程渗透的数学思想为______．

（2）一元二次不等式的解集为______．

（3）请用类似的方法解一元二次不等式：．

16．已知：如图；是的直径，点在上，请用无刻度直尺画图（保留作图痕迹，不写画法）．

图①                         图②

（1）如图①，若M是半圆的中点，且与C点在同侧，画出∠ACB的平分线CN．并说明理由；

（2）如图②，若，画出∠ACB的平分线CP．

17．如图，△ABC的顶点坐标分别为A（0，1），B（3，3），C（1，3）．

（1）将△ABC绕点A逆时针旋转90°得△AB1C1；直接写出点C1的坐标为______．

（2）求在△ABC旋转到△AB1C1的过程中，点C所经过的路径长．

四、解答题（每题8分，共24分）

18．如图，AB为⊙O的直径，AE平分∠BAC，AC⊥PQ于C，交于D．

（1）求证：PQ为⊙O的切线；

（2）若AD＝EC＝4，求⊙O的半径．

19．施工队要修建一个横断面为抛物线的公路隧道，其高度为6米，宽度OM为12米，现在O点为原点，OM所在直线为x轴建立直角坐标系（如图所示）．

（1）直接写出点M及抛物线顶点P的坐标；

（2）求出这条抛物线的函数解析式；

（3）施工队计划在隧道门口搭建一个矩形“脚手架”ABCD，使A、D点在抛物线上，B、C点在地面OM上．为了筹备材料，需求出“脚手架”三根木杆AB、AD、DC的长度之和的最大值是多少？请你帮施工队计算一下．

20．如图，点A在第一象限内，⊙A与x轴相切于点B，与y轴相交于点C，D，连接AB，过点A作AH⊥CD于点H．

（1）求证：四边形ABOH为矩形．

（2）已知⊙A的半径为4，，求弦CD的长．

五、解答题（每题9分，共18分）

21．已知：如图，点P是正方形ABCD内一点，连接PA、PB、PC．

（1）将△PAB绕点B顺时针旋转90°得到△PCB，若AB＝m，PB＝n（n<m）．

求△PAB旋转过程中边PA扫过区域（阴影部分）的面积；

（2）若，，∠APB＝135°，求PC的长．

22．如图，抛物线与x轴交于A，B两点，与y轴交于C点，且经过点（2，－3a），对称轴是直线x＝1，顶点是M．

（1）求抛物线对应的函数表达式；

（2）经过C，M两点作直线与x轴交于点N，在抛物线上是否存在这样的点P，满足以点P，A，C，N为顶点的四边形为平行四边形？若存在，请求出点P的坐标；若不存在，请说明理由；

（3）设直线y＝－x＋3与y轴的交点是D，在线段BD上任取一点E（不与B，D重合），经过A，B，E三点的圆交直线BC于点F，试判断△AEF的形状，并说明理由．

五、解答题（共12分）

23．我们定义：如图1，在△ABC中，把AB绕点A顺时针旋转得到AB'，把AC绕点A逆时针旋转得到，连接，当时，我们称是△ABC的“旋补三角形”，边上的中线AD叫做△ABC的“旋补中线”，点A叫做“旋补中心”．特例感知：

（1）在图2，图3中，是△ABC的“旋补三角形”，AD是△ABC的“旋补中线”．

①如图2，在△ABC为等边三角形时，AD与BC的数量关系为AD＝______BC．

图1                 图2                   图3                  图4

②如图3，当∠BAC＝90°，BC＝18时，则AD长为______．

猜想论证：

（2）在图1中，当△ABC为任意三角形时，猜想AD与BC的数量关系，并给予证明．

（3）如图4，在四边形ABCD中，∠C＝90°，∠D＝150°，BC＝12，，DA＝6，在四边形内部是否存在点P，使△PDC是△PAB的“旋补三角形"？若存在，给予证明，并求△PAB的“旋补中线”长；若不存在，说明理由．