数学八年级上册第十二章 全等三角形12.2 三角形全等的判定当堂达标检测题

第12章 全等三角形

第2课时 12.2三角形全等的判定（1）——边边边

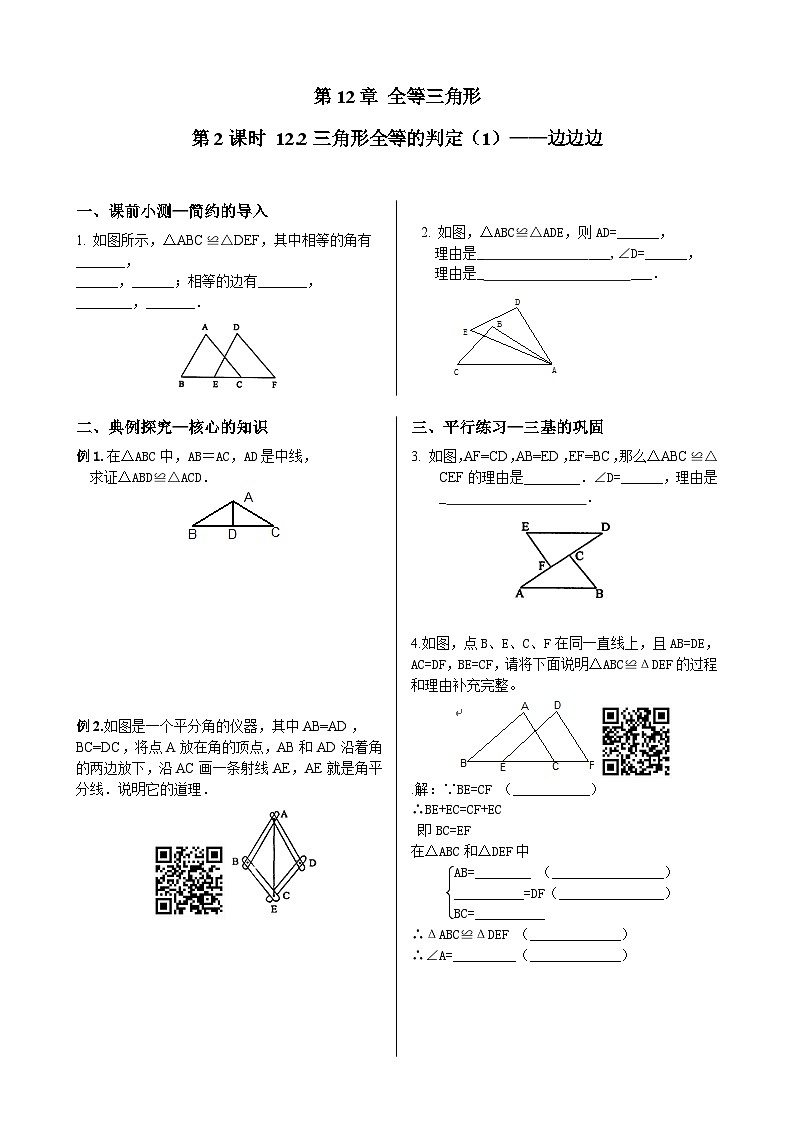
一、课前小测—简约的导入

1. 如图所示，△ABC≌△DEF，其中相等的角有_______，

______，______；相等的边有_______，________，_______．

2. 如图，△ABC≌△ADE，则AD=______，

理由是_               ___,∠D=______，

理由是_                     ___．

二、典例探究—核心的知识

例1.在△ABC中，AB＝AC，AD是中线，

求证△ABD≌△ACD．

例2.如图是一个平分角的仪器，其中AB=AD，BC=DC，将点A放在角的顶点，AB和AD沿着角的两边放下，沿AC画一条射线AE，AE就是角平分线．说明它的道理．

三、平行练习—三基的巩固

3. 如图，AF=CD，AB=ED，EF=BC，那么△ABC≌△CEF的理由是________．∠D=______，理由是_                    ．

4.如图，点B、E、C、F在同一直线上，且AB=DE，AC=DF，BE=CF，请将下面说明ΔABC≌ΔDEF的过程和理由补充完整。

.解：∵BE=CF （___________）

∴BE+EC=CF+EC

即BC=EF

在ΔABC和ΔDEF中

  AB=________ （________________）

  __________=DF（_______________）

  BC=__________

∴ΔABC≌ΔDEF （_____________）

∴∠A=_________（_____________）

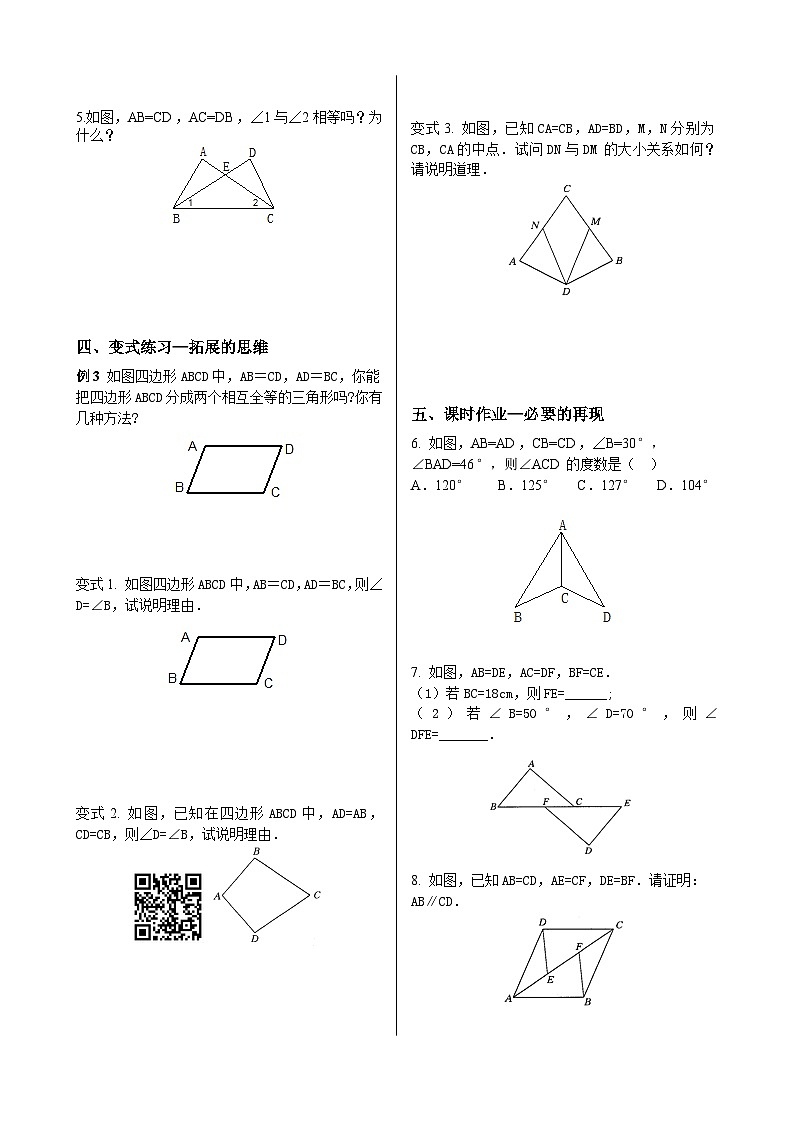
5.如图，AB=CD，AC=DB，∠1与∠2相等吗？为什么？

四、变式练习—拓展的思维

例3 如图四边形ABCD中，AB＝CD，AD＝BC，你能把四边形ABCD分成两个相互全等的三角形吗?你有几种方法?

变式1. 如图四边形ABCD中，AB＝CD，AD＝BC，则∠D=∠B，试说明理由．

变式2. 如图，已知在四边形ABCD中，AD=AB，CD=CB，则∠D=∠B，试说明理由．

变式3. 如图，已知CA=CB，AD=BD，M，N分别为CB，CA的中点．试问DN与DM的大小关系如何？请说明道理．

五、课时作业—必要的再现

6. 如图，AB=AD，CB=CD，∠B=30°，

∠BAD=46°，则∠ACD的度数是（  ）

A．120°    B．125°   C．127°   D．104°

7. 如图，AB=DE，AC=DF，BF=CE．

（1）若BC=18cm，则FE=______;

（2）若∠B=50°，∠D=70°，则∠DFE=_______．

8. 如图，已知AB=CD，AE=CF，DE=BF．请证明：

AB∥CD．

9. 如图，AB=DC，AC=DB，请说明OA与OD相等的理由．

答案:

1.∠A=∠D,∠B=∠DEF, ∠ACB=∠F , AB=DE.  AC=DF. BC=EF.

2.AB，全等三角形对应边相等; ∠B, 全等三角形对应角相等

例1.解：在△ABC中，AD是中线，

     ∴BD=CD，

在△ABD和△ACD中，

△     ABD≌△ACD（SSS）

例2.解：在△ABC和△ADC中，

∴△ABC≌△ADC （SSS）

∴∠BAC＝∠DAC.

3. SSS，∠A, 全等三角形对应角相等。

4.已知,DE,已知,AC,已知，EF, SSS,∠D, 全等三角形对应角相等.

5.解：∠1=∠2，理由如下：连接BC，在△DBC和△ACB中，

∴△DBC≌△ACB（SSS），

∴∠1=∠2 .

例3 解：能把四边形ABCD分成两个相互全等的三角形。方法是：连接AC或BD.

变式1.解：连接AC,

在△ABC和△ADC中，

∴△ABC≌△ADC （SSS）

∴∠B＝∠D。

变式2.连接AC，在△ADC与△ABC中，

    ∵

∴△ADC≌△ABC（SSS），

∴∠D=∠B．

变式3.连接CD．

    在△CAD和△CBD中，

∴△CAD≌△CBD（SSS），∴∠A=∠B．

    又∵AC=CB，M，N分别为CB，CA的中点，

∴AN=BM，

∴△ADN≌△BDM，∴DN=DM．

6.C.

7. (1）18cm  （2）60°

8.证明： ∵AE=CF ∴AF=CE

在△CDE和△ABF中

∴△CDE≌△ABF（SSS），

∴∠DCE=∠BAF，

∴CD∥AB．

9.解：在△ABC和△DCB中

∴△ABC≌△DCB（SSS）

  ∴∠A=∠D（全等三角形的对应角相等）

在△AOB和△DOC中

∴△AOB≌△DOC（AAS） 

∴OA=OD（全等三角形的对应边相等）