江苏省苏州市吴江区汾湖教育集团2023-2024学年九年级上学期第一次阶段测试数学试卷（月考）

这是一份江苏省苏州市吴江区汾湖教育集团2023-2024学年九年级上学期第一次阶段测试数学试卷（月考），文件包含初三数学试卷202310docx、初三数学参考答案202310docx等2份试卷配套教学资源，其中试卷共13页， 欢迎下载使用。
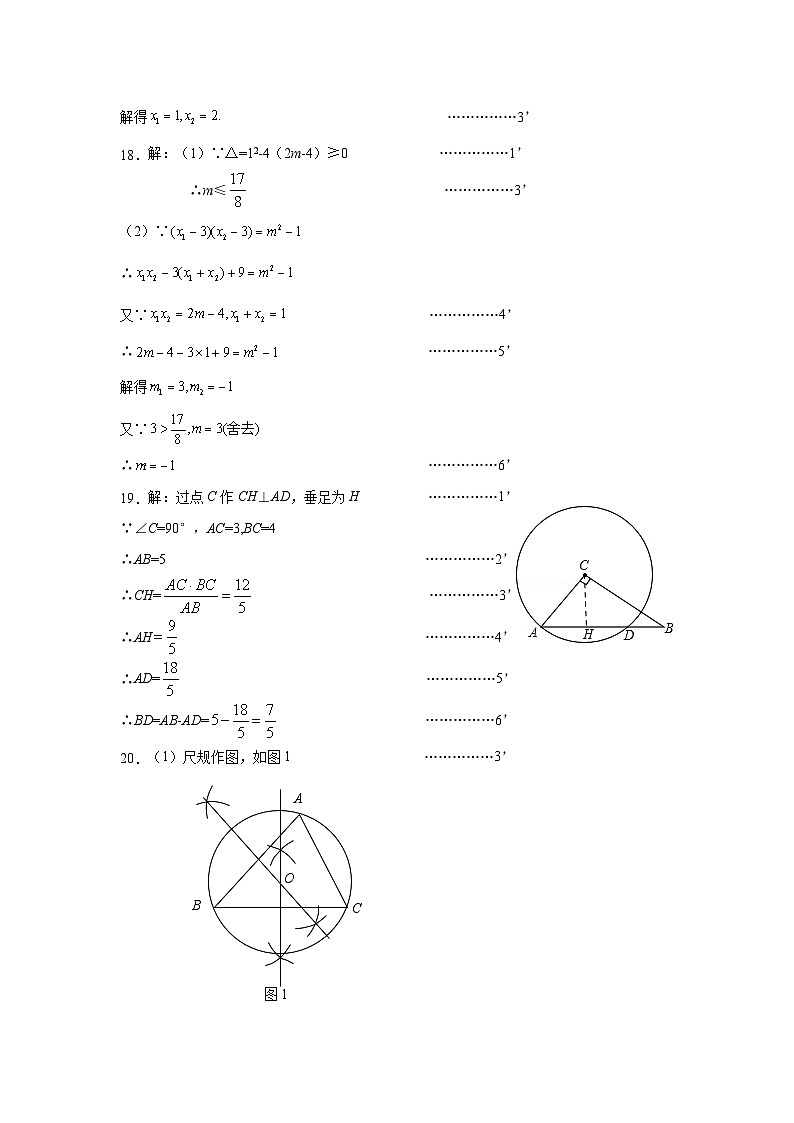
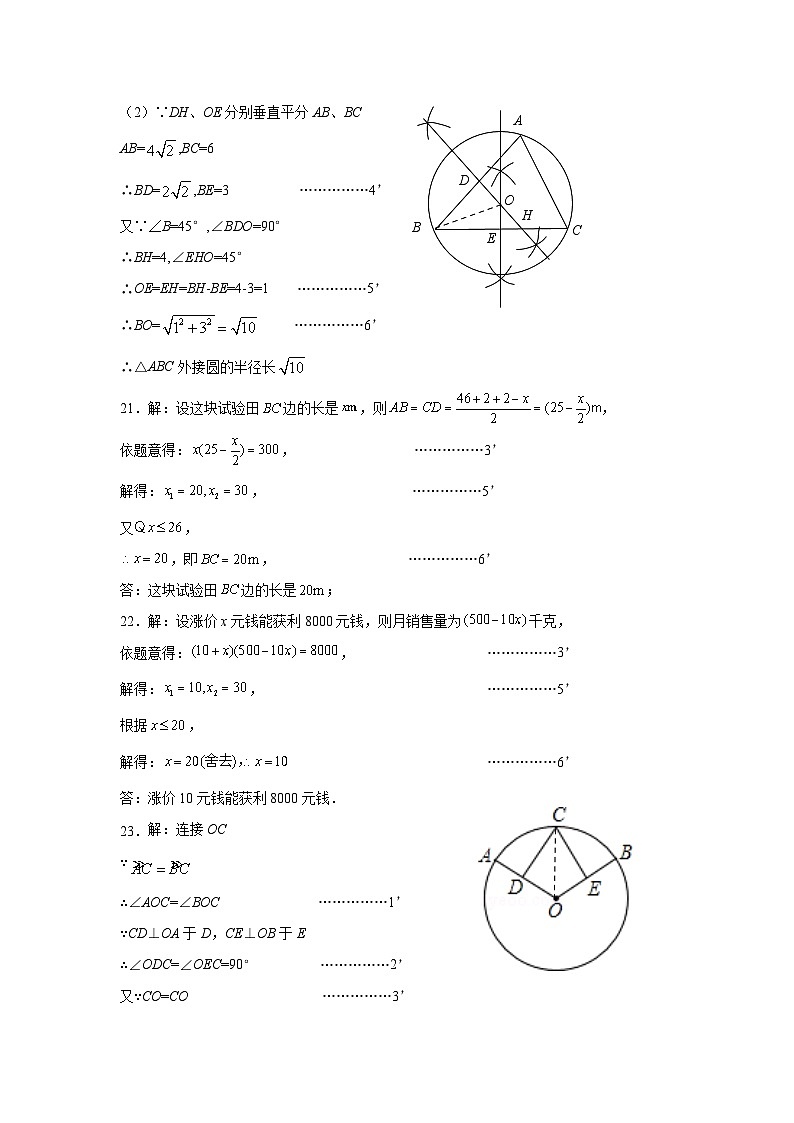
2023-2024学年第一学期第一次阶段测试初三数学                                     2023.10试卷分值：130分  考试用时：120分钟一、选择题（共8小题，每小题3分，共24分.）1．将方程化为一元二次方程的一般形式，其中二次项系数为，一次项系数、常数项分别是（    ）A．， B．， C．， D．，2．下列各式（1﹣x）=0，=0，=0，，x2+3x=0，其中一元二次方程的个数为（    ）A．2个 B．3个 C．4个 D．5个3．关于x的一元二次方程x2+2x﹣m=0有两个实数根，则m的取值范围是（    ）A．m＞﹣1 B．m≥﹣1 C．m≤﹣1且m≠0 D．m≥﹣1且m≠04．唐代李皋发明了“桨轮船”，这种船是原始形态的轮船，是近代明轮航行模式之先导，如图，某桨轮船的轮子被水面截得的弦长，轮子的吃水深度为，则该浆轮船的轮子半径OA为（    ）A．   B．    C．    D．       （第4题）              （第6题）                 （第7题）5．下列命题中： ①在同圆或等圆中，同弦或等弦所对的圆周角相等；②AB、CD是⊙O的弦，若AB＝CD，则AB∥CD ；③垂直于弦的直径平分弦，并且平分弦所对的弧；④圆是轴对称图形，对称轴是圆的每一条直径．其中假命题的是（    ）A．只有③④ B．只有②④ C．只有①④ D．只有①②④6．勒洛三角形是分别以等边三角形的顶点为圆心，以其边长为半径作圆弧，由三段圆弧组成的曲边三角形．如图，该勒洛三角形绕其中心旋转一定角度后能与自身重合，则该角度可以为（    ）A． B． C． D．7．如图，在Rt△ABC中，∠BAC＝90°，AB＝AC，BC＝2，点D是AC边上一动点，连接BD，作AE⊥BD于点E，连接CE，则线段CE长度的最小值为（    ）A．3 B． C． D．18．对于一元二次方程，下列说法：①若，则；②若方程有两个不相等的实根，则方程必有两个不相等的实根；③若是方程的一个根，则一定有成立；④若是一元二次方程的根，则其中正确的：（    ）A．只有① B．只有①② C．①②③ D．只有①②④二、填空题（共8小题，每小题3分，共24分.）9．方程的根是         ．10．方程转化为一元二次方程的一般形式是         ．11．读一读下面的诗词：大江东去浪淘尽，千古风流数人物；而立之年督东吴，早逝英年两位数；十位恰小个位三，个位平方与寿同．诗词大意是周瑜三十岁当上了东吴都督，去世时年龄是两位数，十位数比个位数小3，个位数的平方等于他去世时的年龄，则他去世时年龄为         ．12. 一个矩形，长大于宽，沿长边对折，所得矩形与原矩形相似，则原矩形的长与宽之比为         ．13．如图，⊙O的半径是5，弦AB的长为8，点P在线段AB上运动，则OP的长有          个不同的整数.         （第13题）              （第14题）            （第15题）           （第16题）14．一条排水管的截面如图所示，已知排水管的半径，水面宽，某天下雨后，水面宽度变为，则此时排水管水面上升了         ．15．如图，△ABC中，，截△ABC三条边所得弦长相等，则         ．16．如图，MN是⊙O的直径，OM=2，点A在⊙O上，，B为弧AN的中点， P是直径MN上一动点，则PA+PB的最小值为         .   三、解答题（共11题，共82分）17．（本题满分12分）解方程：（1）；  （2）；（3）；  （4）．     18．（本题满分6分）已知关于的一元二次方程有两个实数根．（1）求的取值范围；（2）若方程的两根满足，求的值．           19.（本题满分6分）如图，∠C=90°，以AC为半径的圆C与AB相交于点D．若AC=3，CB=4，求BD长．            20.（本题满分6分）（1）尺规作图，作出△ABC的外接圆（不写作图过程，但保留作图痕迹）.（2）若AB=,∠B=45°，BC=6，求△ABC外接圆的半径长.             21.（本题满分6分）农民张老伯要尝试种植一种新式水果，在一面长的院墙一边，用长的篱笆围城一块面积为的长方形试验田，为了方便出入在张老伯留了两个宽的门，请问这块试验田边的长是多少？       22.（本题满分6分）某水果投放市场，发现每千克盈利10元时，一个月能售出500千克；若销售价每上涨1元，月销售量就减少10千克；若涨价不得超过20元，请问要涨价多少元，才能获利8000元？     23．（本小题满分6分）如图，在⊙O中，，CD⊥OA于D，CE⊥OB于E，求证：AD=BE．     24．（本小题满分6分）如图，在⊙O中，C是弦AB上的一个动点，连接OC，过点C作CD⊥OC交⊙O于点D．（1）试说明当点C在AB的什么位置时,CD的长取得最大值?（2）若AB=2，求CD长的最大值．   25．（本题满分8分）如图，在矩形中，，，动点P，Q分别从点A、C同时出发，点P以2厘米/秒的速度向终点B移动，点Q以1厘米秒的速度向D移动，当有一点到达终点时，另一点也停止运动，设运动的时间为t秒，问：（1）当t为何值时，点P和点Q距离是？（2）当t为何值时，以点P、Q、D为顶点的三角形是以PQ为腰的等腰三角形．       26．（本题满分8分）阅读材料，解答问题：【材料1】为了解方程，如果我们把看作一个整体，然后设，则原方程可化为，经过运算，原方程的解为，．我们把以上这种解决问题的方法通常叫做换元法．【材料2】已知实数，满足，，且，显然，是方程的两个不相等的实数根，由韦达定理可知，．根据上述材料，解决以下问题：（1）直接应用：方程的解为            ；（2）间接应用：已知实数，满足：，且，求的值．    27．（本题满分12分）如图，在△和△中，，，，连接交于点，交于点，连接．（1）求证；（2）求的度数；（3）若，求证．