
广东省深圳市福田区华富中学2023-2024学年上学期九年级10月月考数学试卷
展开福田区华富中学2023-2024学年第一学期九年级10月月考数学试卷
一.选择题(每题3分,共30分)
1.用配方法解方程x2﹣6x+5=0,配方后可得( )
A.(x+3)2=4 B.(x﹣3)2=4 C.(x﹣3)2=14 D.(x﹣3)2=9
2.如图,矩形ABCD的对角线AC、BD相交于点O,点E是CD的中点,若OE=3,则BC的长为( )
A.3 B.4 C.5 D.6
3.下列说法正确的是( )
A.四边相等的四边形是正方形 B.对角线互相垂直且相等的四边形是正方形
C.对角线互相垂直平分的四边形是菱形 D.对角线相等的四边形是矩形
4.如图,在平面直角坐标系中,菱形ABCD的顶点A,B,C在坐标轴上,若点A、B的坐标分别为(0,2)、(﹣1,0),则点D的坐标为( )
A.(,2) B.(2,) C.(,2) D.(2,)
5.如图,矩形ABCD中,对角线AC,BD交于点O.若∠AOB=60°,BD=8,则AD的长为( )
A.4 B.5 C.3 D.4
6.如图,在菱形ABCD中,∠ABC=70°,对角线AC、BD相交于点O,E为BC中点,则∠COE的度数为( )
A.70° B.65° C.55° D.35°
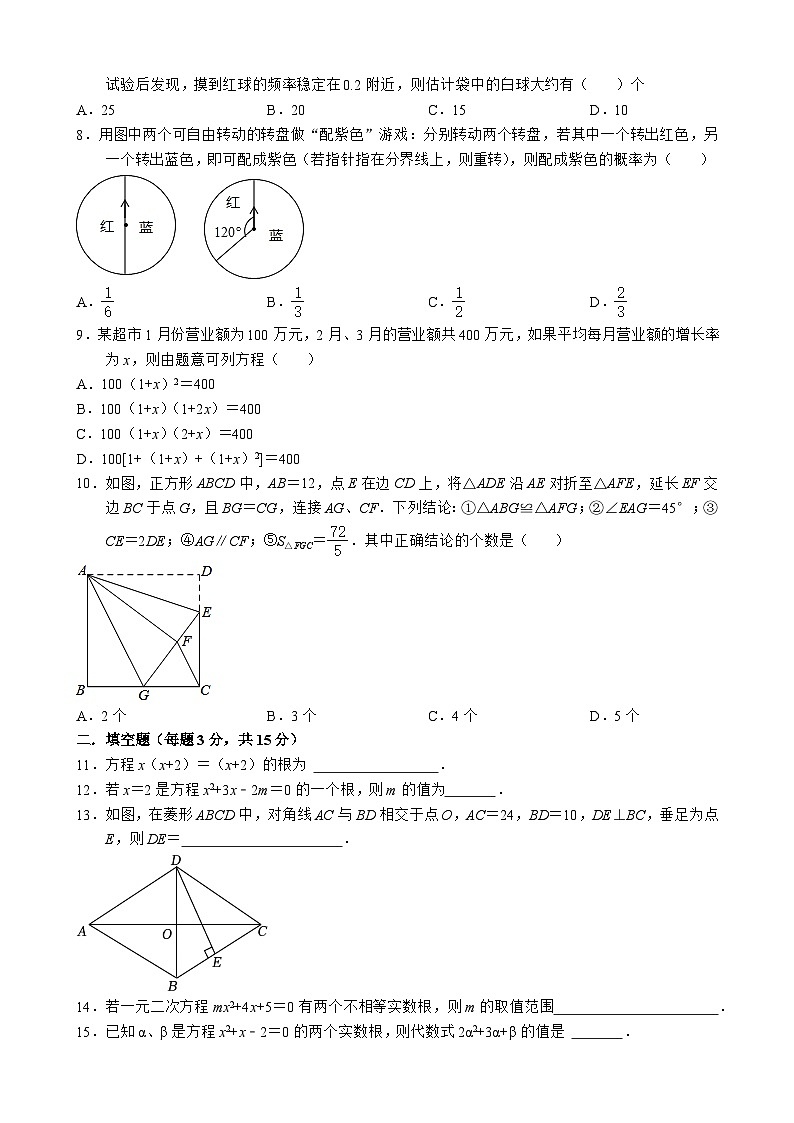
7.在一个不透明的袋子里装有5个红球和若干个白球,它们除颜色外其余完全相同,通过多次摸球试验后发现,摸到红球的频率稳定在0.2附近,则估计袋中的白球大约有( )个
A.25 B.20 C.15 D.10
8.用图中两个可自由转动的转盘做“配紫色”游戏:分别转动两个转盘,若其中一个转出红色,另一个转出蓝色,即可配成紫色(若指针指在分界线上,则重转),则配成紫色的概率为( )
A. B. C. D.
9.某超市1月份营业额为100万元,2月、3月的营业额共400万元,如果平均每月营业额的增长率为x,则由题意可列方程( )
A.100(1+x)2=400
B.100(1+x)(1+2x)=400
C.100(1+x)(2+x)=400
D.100[1+(1+x)+(1+x)2]=400
10.如图,正方形ABCD中,AB=12,点E在边CD上,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,且BG=CG,连接AG、CF.下列结论:①△ABG≌△AFG;②∠EAG=45°;③CE=2DE;④AG∥CF;⑤S△FGC=.其中正确结论的个数是( )
A.2个 B.3个 C.4个 D.5个
二.填空题(每题3分,共15分)
11.方程x(x+2)=(x+2)的根为 .
12.若x=2是方程x2+3x﹣2m=0的一个根,则m的值为 .
13.如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=24,BD=10,DE⊥BC,垂足为点E,则DE= .
14.若一元二次方程mx2+4x+5=0有两个不相等实数根,则m的取值范围 .
15.已知α、β是方程x2+x﹣2=0的两个实数根,则代数式2α2+3α+β的值是 .
三.解答题(共55分)
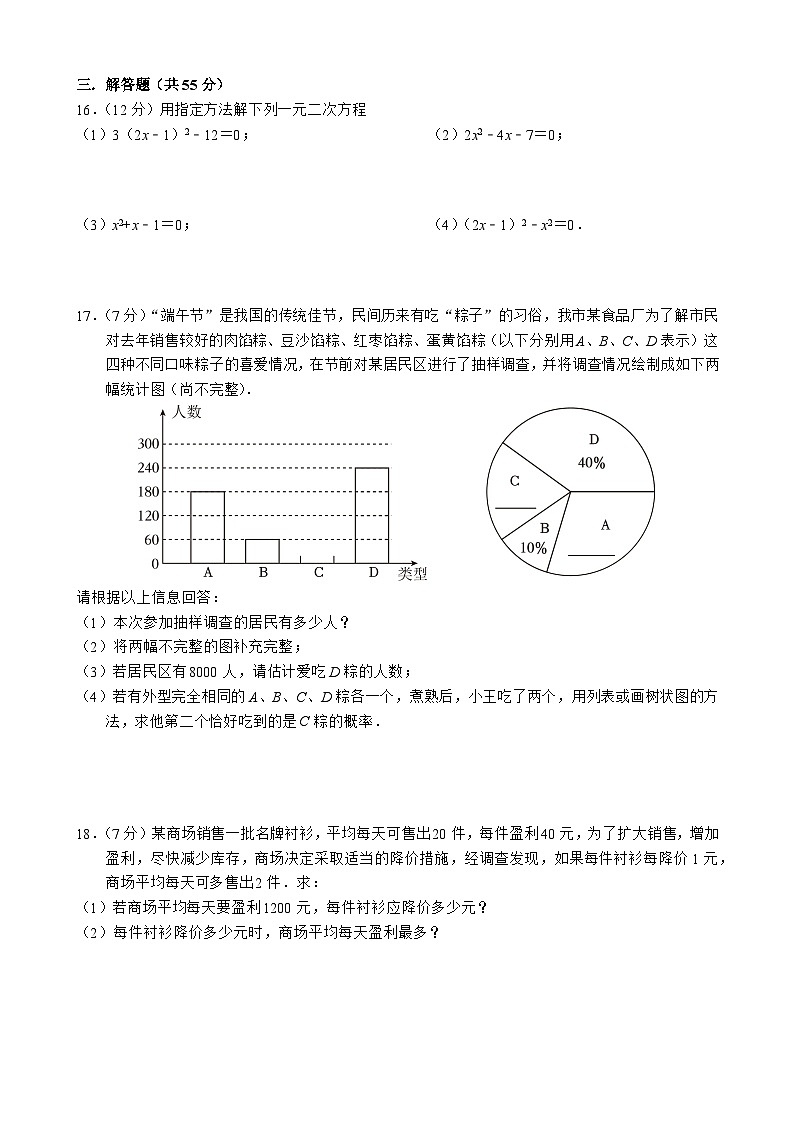
16.(12分)用指定方法解下列一元二次方程
(1)3(2x﹣1)2﹣12=0; (2)2x2﹣4x﹣7=0;
(3)x2+x﹣1=0; (4)(2x﹣1)2﹣x2=0.
17.(7分)“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗,我市某食品厂为了解市民对去年销售较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).
请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数;
(4)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小王吃了两个,用列表或画树状图的方法,求他第二个恰好吃到的是C粽的概率.
18.(7分)某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件.求:
(1)若商场平均每天要盈利1200元,每件衬衫应降价多少元?
(2)每件衬衫降价多少元时,商场平均每天盈利最多?
19.(6分)已知关于x,y的方程组与的解相同.
(1)求a,b的值;
(2)若一个三角形的一条边的长为2,另外两条边的长是关于x的方程x2+ax+b=0的解.试判断该三角形的形状,并说明理由.
20.(7分)如图,已知:在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF∥AE.
(1)求证:四边形BECF是菱形;
(2)当∠A= °时,四边形BECF是正方形;
(3)在(2)的条件下,若AC=4,则四边形ABFC的面积为 .
21.(8分)如图,△ABC中,∠C=90°,AC=8cm,BC=6cm,动点D从点A出发以4cm/s速度向点C移动,同时动点E从C出发以3cm/s的速度向点B移动,设它们的运动时间为ts.
(1)根据题意知:CE= ,CD= ;(用含t的代数式表示)
(2)t为何值时,△CDE的面积等于四边形ABED的面积的?
(3)点D、E运动时,DE的长可以是4cm吗?如果可以,请求出t的值,如果不可以,请说明理由.
22.(8分)小明学习了平行四边形这一章后,对特殊四边形的探究产生了兴趣,发现另外一类特殊四边形,如图1,我们把两条对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解:在平行四边形、矩形、菱形、正方形中,一定是垂美四边形的是
(2)性质探究:通过探究,直接写出垂直四边形ABCD的面积S与两对角线AC,BD之间的数量关系: .
(3)问题解决:如图2,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CG,BE,GE,已知AC=4,AB=5.
①求证:四边形BCGE为垂美四边形;
②求出四边形BCGE的面积.
华富中学10月月考参考答案与试题解析
一.选择题(共10小题)
1.用配方法解方程x2﹣6x+5=0,配方后可得( )
A.(x+3)2=4 B.(x﹣3)2=4 C.(x﹣3)2=14 D.(x﹣3)2=9
【解答】解:x2﹣6x+5=0,
x2﹣6x=﹣5,
x2﹣6x+9=4,
(x﹣3)2=4.
故选:B.
2.如图,矩形ABCD的对角线AC、BD相交于点O,点E是CD的中点,若OE=3,则BC的长为( )
A.3 B.4 C.5 D.6
【解答】解:∵四边形ABCD为矩形,
∴DO=BO,
∵点E是CD的中点,OE=3,
∴BC=2OE=6,
故选:D.
3.下列说法正确的是( )
A.四边相等的四边形是正方形
B.对角线互相垂直且相等的四边形是正方形
C.对角线互相垂直平分的四边形是菱形
D.对角线相等的四边形是矩形
【解答】解:A、四边相等的四边形是菱形,说法错误,不符合题意;
B、对角线平分互相垂直且相等的四边形是正方形,说法错误,不符合题意;
C、对角线互相垂直平分的四边形是菱形,说法正确,符合题意;
D、对角线平分且相等的四边形是矩形,说法错误,不符合题意;
故选:C.
4.如图,在平面直角坐标系中,菱形ABCD的顶点A,B,C在坐标轴上,若点A、B的坐标分别为(0,2)、(﹣1,0),则点D的坐标为( )
A.(,2) B.(2,) C.(,2) D.(2,)
【解答】解:∵点A、B的坐标分别为(0,2)、(﹣1,0),
∴OB=1,AO=2,
∴AB==,
∵四边形ABCD是菱形,
∴AD=AB=,AD∥BC,
∴点D坐标为(,2),
故选A.
5.如图,矩形ABCD中,对角线AC,BD交于点O.若∠AOB=60°,BD=8,则AD的长为( )
A.4 B.5 C.3 D.4
【解答】解:∵四边形ABCD是矩形,BD=8,
∴AC=BD=8,∠ABC=90°,
∴OA=OB=4,
∵∠AOB=60°,
∴△ABO是等边三角形,
∴AB=OA=4,
∴AD==4,
故选:D.
6.如图,在菱形ABCD中,∠ABC=70°,对角线AC、BD相交于点O,E为BC中点,则∠COE的度数为( )
A.70° B.65° C.55° D.35°
【解答】解:在菱形ABCD中,AC⊥BD,∠ABC=70°,
∴∠BOC=90°,∠COB=∠ABC=35°,
∴∠OCB=90°﹣35°=55°,
∵E为BC的中点,
∴OE=CE,
∴∠COE=∠OCB=55°.
故选:C.
7.在一个不透明的袋子里装有5个红球和若干个白球,它们除颜色外其余完全相同,通过多次摸球试验后发现,摸到红球的频率稳定在0.2附近,则估计袋中的白球大约有( )个
A.25 B.20 C.15 D.10
【解答】解:设白球个数为x个,
∵摸到红色球的频率稳定在0.2左右,
∴口袋中得到红色球的概率为0.2,
∴=0.2,
解得:x=20,
即袋中的白球大约有20个;
故选:B.
8.用图中两个可自由转动的转盘做“配紫色”游戏:分别转动两个转盘,若其中一个转出红色,另一个转出蓝色,即可配成紫色(若指针指在分界线上,则重转),则配成紫色的概率为( )
A. B. C. D.
【解答】解:列表如下:
红
蓝
红
(红,红)
(蓝,红)
蓝
(红,蓝)
(蓝,蓝)
蓝
(红,蓝)
(蓝,蓝)
由表格知共有6种等可能出现的结果数,其中能配成紫色的结果数有3种,
则P(配成紫色)==,
故选:C.
9.某超市1月份营业额为100万元,2月、3月的营业额共400万元,如果平均每月营业额的增长率为x,则由题意可列方程( )
A.100(1+x)2=400
B.100(1+x)(1+2x)=400
C.100(1+x)(2+x)=400
D.100[1+(1+x)+(1+x)2]=400
【解答】解:设平均每月增长率为x,
100[(1+x)+(1+x)2]=400.
即:100(1+x)(2+x)=400,
故选:C.
10.如图,正方形ABCD中,AB=12,点E在边CD上,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,且BG=CG,连接AG、CF.下列结论:①△ABG≌△AFG;②∠EAG=45°;③CE=2DE;④AG∥CF;⑤S△FGC=.其中正确结论的个数是( )
A.2个 B.3个 C.4个 D.5个
【解答】解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD=12,∠B=∠GCE=∠D=90°,
由折叠的性质得:AF=AD,∠AFE=∠D=90°,
∴∠AFG=90°=∠B,AB=AF,
在Rt△ABG和Rt△AFG中,
,
∴Rt△ABG≌Rt△AFG(HL),故①正确;
∴∠BAG=∠FAG,
由折叠可得,∠DAE=∠FAE,
∴∠EAG=∠BAD=45°,故②正确;
由题意得:EF=DE,BG=CG=6=GF,
设DE=EF=x,则CE=12﹣x.
在直角△ECG中,根据勾股定理,得CE2+CG2=GE2,
即(12﹣x)2+62=(x+6)2,
解得:x=4,
∴DE=4,CE=8,
∴CE=2DE,故③正确;
∵CG=BG,BG=GF,
∴CG=GF,
∴∠GFC=∠GCF.
又∵Rt△ABG≌Rt△AFG,
∴∠AGB=∠AGF,
∵∠AGB+∠AGF=2∠AGB=∠GFC+∠GCF=2∠GCF,
∴∠AGB=∠GCF,
∴AG∥CF,故④正确;
∵S△GCE=GC•CE=×6×8=24,
∵GF=6,EF=4,△GFC和△FCE等高,
∴S△GFC:S△FCE=3:2,
∴S△GFC=×24=,故⑤正确.
故选:D.
二.填空题(共5小题)
11.方程x(x+2)=(x+2)的根为 x1=1,x2=﹣2 .
【解答】解:x(x+2)﹣(x+2)=0,
(x+2)(x﹣1)=0,
x+2=0或x﹣1=0,
x=﹣2或1.
故答案为:x1=﹣2,x2=1.
12.若x=2是方程x2+3x﹣2m=0的一个根,则m的值为 5 .
【解答】解:把x=2代入,得
22+3×2﹣2m=0,
解得:m=5.
故答案为:5.
13.如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=24,BD=10,DE⊥BC,垂足为点E,则DE= .
【解答】解:∵四边形ABCD是菱形,
∴AD=BC,AC⊥BD,AO=OC,DO=BO,
∵AC=24,BD=10,
∴AO=12,OD=5,由勾股定理得:AD=13,
∴BC=13,
∴S菱形ABCD=AC•BD=BC×DE,
∴×24×10=13×DE,
解得:DE=,
故答案为:.
14.若一元二次方程mx2+4x+5=0有两个不相等实数根,则m的取值范围 m<且m≠0 .
【解答】解:∵一元二次方程mx2+4x+5=0有两个不相等实数根,
∴Δ=b2﹣4ac=42﹣4×m×5=16﹣20m>0,
解得:m<,
∵m≠0,
∴m的取值范围为:m< 且m≠0.
故答案为:m< 且m≠0.
15.已知α、β是方程x2+x﹣2=0的两个实数根,则代数式2α2+3α+β的值是 3 .
【解答】解:∵α、β是方程x2+x﹣2=0的两个实数根,
∴α+β=﹣1,αβ=﹣2,α2+α﹣2=0,
∴α2+α=2,
∴2α2+3α+β
=2(α2+α)+α+β
=2×2﹣1
=3.
故答案为:3.
三.解答题(共7小题)
16.用指定方法解下列一元二次方程
(1)3(2x﹣1)2﹣12=0;
(2)2x2﹣4x﹣7=0;
(3)x2+x﹣1=0;
(4)(2x﹣1)2﹣x2=0.
【解答】解:(1)3(2x﹣1)2﹣12=0,
移项,得 3(2x﹣1)2=12,
两边都除以3,得(2x﹣1)2=4,
两边开平方,得2x﹣1=±2,
移项,得2x=1±2,
解得:x1=,x2=﹣;
(2)2x2﹣4x﹣7=0,
两边都除以2,得x2﹣2x﹣=0,
移项,得x2﹣2x=,
配方,得x2﹣2x+1=,即(x﹣1)2=,
解得:x﹣1=±,
即x1=1+,x2=1﹣;
(3)x2+x﹣1=0,
这里a=1,b=1,c=﹣1,
∵b2﹣4ac=12﹣4×1×(﹣1)=5,
∴x=,
解得:x1=,x2=;
(4)(2x﹣1)2﹣x2=0,
方程左边因式分解,得(2x﹣1+x)(2x﹣1﹣x)=0,即(3x﹣1)(x﹣1)=0,
解得:x1=,x2=1.
17.“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗,我市某食品厂为了解市民对去年销售较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).
请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数;
(4)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小王吃了两个,用列表或画树状图的方法,求他第二个恰好吃到的是C粽的概率.
【解答】解:(1)60÷10%=600(人)
答:本次参加抽样调查的居民由600人;
(2)600﹣180﹣60﹣240=120,120÷600×100%=20%,100%﹣10%﹣40%﹣20%=30%
补全统计图如图所示:
(3)8000×40%=3200(人)
答:该居民区有8000人,估计爱吃D粽的人有3200人.
(4)如图:
共有12种等可能情形,第二个恰好吃到的是C粽有3种情形,
P(C粽)=.
18.某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件.求:
(1)若商场平均每天要盈利1200元,每件衬衫应降价多少元?
(2)每件衬衫降价多少元时,商场平均每天盈利最多?
【解答】解:(1)设每件衬衫降价x元,商场平均每天盈利y元,
则y=(40﹣x)(20+2x)=800+80x﹣20x﹣2x2=﹣2x2+60x+800,
当y=1200时,1200=(40﹣x)(20+2x),
解得 x1=10,x2=20,
经检验,x1=10,x2=20都是原方程的解,但要尽快减少库存,
所以x=20,
答:每件衬衫应降价20元;
(2)∵y=﹣2x2+60x+800=﹣2(x﹣15)2+1250,
∴当x=15时,y的最大值为1250,
答:当每件衬衫降价15元时,专卖店每天获得的利润最大,最大利润是1250元.
19.已知关于x,y的方程组与的解相同.
(1)求a,b的值;
(2)若一个三角形的一条边的长为2,另外两条边的长是关于x的方程x2+ax+b=0的解.试判断该三角形的形状,并说明理由.
【解答】解:(1)由题意得,关于x,y的方程组的相同解,就是方程组的解,
解得,,代入原方程组得,a=﹣4,b=12;
(2)该三角形是等腰直角三角形,理由如下:
当a=﹣4,b=12时,关于x的方程x2+ax+b=0就变为x2﹣4x+12=0,
解得,x1=x2=2,
又∵(2)2+(2)2=(2)2,
∴以2、2、2为边的三角形是等腰直角三角形.
20.如图,已知:在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF∥AE.
(1)求证:四边形BECF是菱形;
(2)当∠A= 45 °时,四边形BECF是正方形;
(3)在(2)的条件下,若AC=4,则四边形ABFC的面积为 12 .
【解答】(1)证明:∵EF垂直平分BC,
∴BF=FC,BE=EC,
∴∠FCB=∠FBC,
∵CF∥AE
∴∠FCB=∠CBE,
∴∠FBC=∠CBE,
∵∠FDB=∠EDB,BD=BD,
∴△FDB≌△EDB(ASA),
∴BF=BE,
∴BE=EC=FC=BF,
∴四边形BECF是菱形;
(2)解:当∠A=45°时,四边形BECF是正方形,理由如下:
若四边形BECF是正方形,则∠ECB=∠FCB=45°,
∵∠ACB=90°,
∴∠ACE=45°,
∵∠A=45°,
∴∠AEC=90°,
由(1)知四边形BECF是菱形,
∴四边形BECF是正方形;
故答案为:45;
(3)解:由(2)知,四边形BECF是正方形,AE=BE=CE=2,
∴四边形ABFC的面积为=12,
故答案为:12.
21.如图,△ABC中,∠C=90°,AC=8cm,BC=6cm,动点D从点A出发以4cm/s速度向点C移动,同时动点E从C出发以3cm/s的速度向点B移动,设它们的运动时间为ts.
(1)根据题意知:CE= 3tcm ,CD= (8﹣4t)cm ;(用含t的代数式表示)
(2)t为何值时,△CDE的面积等于四边形ABED的面积的?
(3)点D、E运动时,DE的长可以是4cm吗?如果可以,请求出t的值,如果不可以,请说明理由.
【解答】解:(1)∵动点D、E同时出发,动点E从C出发向点B移动,
∴CE=3tcm,
∵动点D从点A出发向点C移动,
∴CD=(8﹣4t)cm,
故答案为:3tcm,(8﹣4t)cm.
(2)当△CDE的面积等于四边形ABED的面积的时,则△CDE的面积等于△ABC的面积的,
根据题意得×3t(8﹣4t)=××8×6,
整理得t2﹣2t+1=0,
解得t1=t2=1,
答:t=1,即运动1秒时,△CDE的面积等于四边形ABED的面积的.
(3)不可以,理由如下:
如果可以,则由勾股定理得(3t)2+(8﹣4t)2=42,
整理得25t2﹣64t+48=0,
∵Δ=(﹣64)2﹣4×25×48=﹣704<0,
∴该方程没有实数根,
∴DE的长不可以是4cm.
22.小明学习了平行四边形这一章后,对特殊四边形的探究产生了兴趣,发现另外一类特殊四边形,如图1,我们把两条对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解:在平行四边形、矩形、菱形、正方形中,一定是垂美四边形的是 菱形、正方形
(2)性质探究:通过探究,直接写出垂直四边形ABCD的面积S与两对角线AC,BD之间的数量关系: AC•BD .
(3)问题解决:如图2,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CG,BE,GE,已知AC=4,AB=5.
①求证:四边形BCGE为垂美四边形;
②求出四边形BCGE的面积.
【解答】(1)解:在平行四边形、矩形、菱形、正方形中,两条对角线互相垂直的四边形是菱形、正方形,
∴菱形和正方形一定是垂美四边形;
故答案为:菱形、正方形;
(2)解:如图1所示:
∵四边形ABCD的面积=△ABC的面积+△ADC的面积=AC•BO+AC•DO=AC(BO+DO)=AC•BD;
故答案为:AC•BD;
(3)①证明:连接CG、BE,如图2所示:
∵四边形ACFG和四边形ABDE是正方形,
∴∠F=∠CAG=∠BAE=90°,FG=AG=AC=CF,AB=AE,
∴∠CAG+∠BAC=∠BAE+∠BAC,
即∠GAB=∠CAE,
在△GAB和△CAE中,
,
∴△GAB≌△CAE(SAS),
∴BG=CE,∠ABG=∠AEC,
又∵∠AEC+∠AME=90°,∠AME=∠BMN,
∴∠ABG+∠BMN=90°,
∴∠BNM=90°,
∴BG⊥CE,
∴四边形BCGE为垂美四边形;
②解:∵FG=CF=AC=4,∠ACB=90°,AB=5,
∴BC==3,
∴BF=BC+CF=7,
在Rt△BFG中,BG===,
∴CE=BG=,
∵四边形BCGE为垂美四边形,
∴四边形BCGE的面积=BG•CE=.
2023-2024学年广东省深圳市福田区红岭中学九年级(上)月考数学试卷(12月份)(含解析): 这是一份2023-2024学年广东省深圳市福田区红岭中学九年级(上)月考数学试卷(12月份)(含解析),共21页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
+广东省深圳市福田区华富中学2023-2024学年九年级上学期期中数学试卷: 这是一份+广东省深圳市福田区华富中学2023-2024学年九年级上学期期中数学试卷,共5页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023-2024学年广东省深圳市福田区华富中学九年级(上)月考数学试卷(10月份)(含解析): 这是一份2023-2024学年广东省深圳市福田区华富中学九年级(上)月考数学试卷(10月份)(含解析),共11页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。












