广东省深圳市教育科学研究院实验学校（光明）2023-2024学年上学期九年级10月月考数学试卷

这是一份广东省深圳市教育科学研究院实验学校（光明）2023-2024学年上学期九年级10月月考数学试卷，共16页。试卷主要包含了使分式有意义的条件是等内容，欢迎下载使用。
深圳教科院实验学校（光明）2023-2024学年第一学期九年级10月月考数学试卷

一．选择题（每题3分，共30分）
1．已知a＞b，则下列不等式一定成立的是（　　）
A．a+c＜b+c B．a﹣3＞b﹣3
C．am＞bm D．a（c2+1）＜b（c2+1）
2．使分式有意义的条件是（　　）
A．x＝±1 B．x≠±1 C．x≠1 D．x≠﹣1
3．如图，把线段AB经过平移得到线段CD，其中A，B的对应点分别为C，D．已知A（﹣1，0），B（﹣2，3），C（2，1），则点D的坐标为（　　）

A．（1，4） B．（1，3） C．（2，4） D．（2，3）
4．一次函数y1＝kx+b和y2＝2x的图象如图所示，则kx+b≥2x的解集是（　　）

A．x≥1 B．x≤2 C．x＜1 D．x≤1
5．关于x的一元二次方程x2+2x﹣3＝0的根的情况是（　　）
A．有两个不相等的实数根 B．只有一个实数根
C．有两个相等的实数根 D．没有实数根
6．如图，在△ABC中，点D、点E分别是AB，AC的中点，点F是DE上一点，且∠AFC＝90°，若BC＝12，AC＝8，则DF的长为（　　）

A．1 B．2 C．3 D．4
7．如图，在▱ABCD中，DE平分∠ADC，AD＝8，BE＝3，则▱ABCD的周长是（　　）

A．16 B．14 C．26 D．24
8．如图，在△ABC中，点D，E，F分别是AB，BC，AC的中点，则下列四个判断中不一定正确的是（　　）

A．四边形ADEF一定是平行四边形
B．若∠B+∠C＝90°，则四边形ADEF是矩形
C．若四边形ADEF是菱形，则△ABC是等边三角形
D．若四边形ADEF是正方形，则△ABC是等腰直角三角形
9．如图，在矩形ABCD中，点A的坐标是（1，0），点C的坐标是（﹣2，4），则BD的长是（　　）


A． B．5 C．3 D．4
10．如图，正方形ABCD外取一点E，连接AE、BE、DE．过点A作AE的垂线交DE于点P，若AE＝AP＝1，PB＝．下列结论：①EB⊥ED；②点B到直线DE的距离为； ③S△APD+S△APB＝； ④S正方形ABCD＝2．其中正确结论的序号是（　　）

A．①③④ B．①②③ C．②③④ D．①②③④
二．填空题（每题3分，共15分）
11．分解因式：ab2+4ab+4a＝　 　．
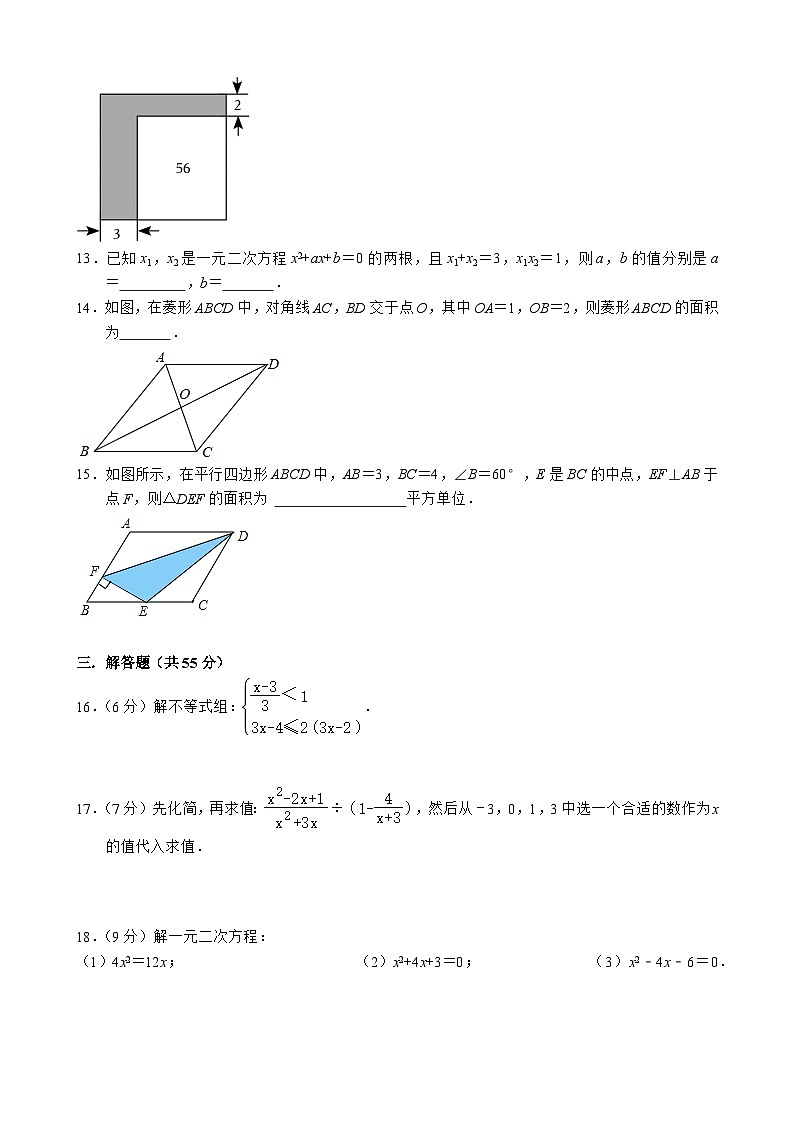
12．公园原有一块正方形空地，后来从这块空地上划出部分区域栽种鲜花（阴影部分），原空地一边减少了3m，另一边减少了2m，剩余空地面积为56m2，设正方形空地原来的边长为xm，则可列方程为 　 　．

13．已知x1，x2是一元二次方程x2+ax+b＝0的两根，且x1+x2＝3，x1x2＝1，则a，b的值分别是a＝　 　，b＝　 　．
14．如图，在菱形ABCD中，对角线AC，BD交于点O，其中OA＝1，OB＝2，则菱形ABCD的面积为　 　．

15．如图所示，在平行四边形ABCD中，AB＝3，BC＝4，∠B＝60°，E是BC的中点，EF⊥AB于点F，则△DEF的面积为 　 　平方单位．


三．解答题（共55分）
16．（6分）解不等式组：．


17．（7分）先化简，再求值：，然后从﹣3，0，1，3中选一个合适的数作为x的值代入求值．



18．（9分）解一元二次方程：
（1）4x2＝12x； （2）x2+4x+3＝0； （3）x2﹣4x﹣6＝0．



19．（8分）已知关于x的一元二次方程x2﹣6x+2m﹣1＝0有x1，x2两实数根．
（1）若x1＝1，求x2及m的值；
（2）是否存在实数m，满足（x1﹣1）（x2﹣1）＝？若存在，求出实数m的值；若不存在，请说明理由．






20．（7分）如图，在平行四边形ABCD中，对角线AC、BD交于点O，点E为BC的中点，EF⊥CD于点F，点G为CD上一点，连接OG，OE，且OG∥EF．
（1）求证：四边形OEFG为矩形；
（2）若AD＝15，OG＝6，∠ABD＝45°，求AB的长．







21．（8分）端午节前夕，某超市从厂家分两次购进蛋黄粽子、红豆粽子，两次进货时，两种粽子的进价不变．第一次购进蛋黄粽子60袋和红豆粽子90袋，总费用为4800元；第二次购进蛋黄粽子40袋和红豆粽子80袋，总费用为3600元．
（1）求蛋黄粽子、红豆粽子每袋的进价各是多少元？
（2）当蛋黄粽子销售价为每袋70元时，每天可售出20袋，为了促销，该超市决定对蛋黄粽子进行降价销售，经市场调研，若每袋的销售价每降低1元，则每天的销售量将增加5袋．当蛋黄粽子每袋的销售价为多少元时，每天售出蛋黄粽子所获得的利润为220元？









22．（10分）如图，在平面直角坐标系xOy中，直线AB：y＝﹣x+3与直线CD：y＝kx﹣2相交于点M（4，a），分别交坐标轴于点A，B，C，D．
（1）求a和k的值；
（2）如图，点P是直线CD上的一个动点，设点P的横坐标为m，当S△PBM＝20成立时，求点P的坐标；
（3）直线AB上有一点F，在平面直角坐标系内找一点N，使得以BF为一边，以点B，D，F，N为顶点的四边形是菱形，请直接写出符合条件的点N的坐标．


深圳教科院学校光明部10月月考参考答案与试题解析
一．选择题（共10小题）
1．已知a＞b，则下列不等式一定成立的是（　　）
A．a+c＜b+c B．a﹣3＞b﹣3
C．am＞bm D．a（c2+1）＜b（c2+1）
【解答】解：A、∵a＞b，
∴a+c＞b+c，
故A不符合题意；
B、∵a＞b，
∴a﹣3＞b﹣3，
故B符合题意；
C、∵a＞b，m＞0，
∴am＞bm，
故C不符合题意；
D、∵a＞b，
∴a（c2+1）＞b（c2+1），
故D不符合题意；
故选：B．
2．使分式有意义的条件是（　　）
A．x＝±1 B．x≠±1 C．x≠1 D．x≠﹣1
【解答】解：分式有意义的条件是：x﹣1≠0，
解得：x≠1．
故选：C．
3．如图，把线段AB经过平移得到线段CD，其中A，B的对应点分别为C，D．已知A（﹣1，0），B（﹣2，3），C（2，1），则点D的坐标为（　　）

A．（1，4） B．（1，3） C．（2，4） D．（2，3）
【解答】解：∵A（﹣1，0）的对应点C的坐标为（2，1），
∴平移规律为横坐标加3，纵坐标加1，
∵点B（﹣2，3）的对应点为D，
∴D的坐标为（1，4）．
故选：A．
4．一次函数y1＝kx+b和y2＝2x的图象如图所示，则kx+b≥2x的解集是（　　）

A．x≥1 B．x≤2 C．x＜1 D．x≤1
【解答】解：当x≤1时，kx+b≥2x，
所以不等式kx+b≥2x的解集为x≤1．
故选：D．
5．关于x的一元二次方程x2+2x﹣3＝0的根的情况是（　　）
A．有两个不相等的实数根 B．只有一个实数根
C．有两个相等的实数根 D．没有实数根
【解答】解：在方程x2+2x﹣3＝0中，Δ＝22﹣4×1×（﹣3）＝16＞0，
∴方程x2+2x﹣3＝0有两个不相等的实数根．
故选：A．
6．如图，在△ABC中，点D、点E分别是AB，AC的中点，点F是DE上一点，且∠AFC＝90°，若BC＝12，AC＝8，则DF的长为（　　）

A．1 B．2 C．3 D．4
【解答】解：∵点D、点E分别是AB，AC的中点，
∴DE是△ABC的中位线，
∴DE＝BC，
∵BC＝12，
∴DE＝6，
在Rt△AFC中，∠AFC＝90°，点E是AC的中点，AC＝8，
∴FE＝AC＝4，
∴DF＝DE﹣FE＝6﹣4＝2，
故选：B．
7．如图，在▱ABCD中，DE平分∠ADC，AD＝8，BE＝3，则▱ABCD的周长是（　　）

A．16 B．14 C．26 D．24
【解答】解：∵在▱ABCD中，AD＝8，
∴BC＝AD＝8，AD∥BC，
∴CE＝BC﹣BE＝8﹣3＝5，∠ADE＝∠CED，
∵DE平分∠ADC，
∴∠ADE＝∠CDE，
∴∠CDE＝∠CED，
∴CD＝CE＝5，
∴▱ABCD的周长是：2（AD+CD）＝26．
故选：C．
8．如图，在△ABC中，点D，E，F分别是AB，BC，AC的中点，则下列四个判断中不一定正确的是（　　）

A．四边形ADEF一定是平行四边形
B．若∠B+∠C＝90°，则四边形ADEF是矩形
C．若四边形ADEF是菱形，则△ABC是等边三角形
D．若四边形ADEF是正方形，则△ABC是等腰直角三角形
【解答】解：∵点D，E，F分别是AB，BC，AC的中点，
∴EF＝AD＝DB＝AB，DE＝AF＝FC＝AC，EF∥AB，DE∥AC
∴四边形ADEF是平行四边形
故A正确，
若∠B+∠C＝90°，则∠A＝90°
∴四边形ADEF是矩形，
故B正确，
若四边形ADEF是菱形，则AD＝AF，
∴AB＝AC
∴△ABC是等腰三角形
故C不一定正确
若四边形ADEF是正方形，则AD＝AF，∠A＝90°
∴AB＝AC，∠A＝90°
∴△ABC是等腰直角三角形
故D正确
故选：C．
9．如图，在矩形ABCD中，点A的坐标是（1，0），点C的坐标是（﹣2，4），则BD的长是（　　）


A． B．5 C．3 D．4
【解答】解：连接AC，如图：
∵四边形ABCD是矩形，
∴BD＝AC，
∵点A的坐标是（1，0），点C的坐标是（﹣2，4），
∴AC＝＝5，
∴BD＝AC＝5，
故选：B．

10．如图，正方形ABCD外取一点E，连接AE、BE、DE．过点A作AE的垂线交DE于点P，若AE＝AP＝1，PB＝．下列结论：①EB⊥ED；②点B到直线DE的距离为； ③S△APD+S△APB＝； ④S正方形ABCD＝2．其中正确结论的序号是（　　）

A．①③④ B．①②③ C．②③④ D．①②③④
【解答】解：如图，∵四边形ABCD是正方形，
∴AD＝AB，∠BAD＝ADC＝90°，
∵AE⊥AP，
∴∠EAP＝90°，
∴∠BAE+∠BAP＝∠BAP+∠DAP＝90°，
∴∠BAE＝∠DAP，
∵AE＝AP＝1，
∴△ABE≌△ADP（SAS），
∴∠AEB＝∠APD，BE＝DP，
∵△AEP是等腰直角三角形，
∴∠AEP＝∠APE＝45°，EP＝AE＝，
∴∠APD＝180°﹣∠APE＝180°﹣45°＝135°，
∴∠AEB＝135°，
∴∠BED＝∠AEB﹣∠AEP＝135°﹣45°＝90°，
∴EB⊥ED，
∴①正确；
∴BE＝＝＝1＝AE，
∴②不正确；
∵△ABE≌△ADP，
∴S△ABE＝S△ADP，
∵∠BAP＝90°，AE＝AP＝1，PB＝，
∴EP＝，∠AEP＝45°，
∵∠AEB＝135°，
∴∠BEP＝135°﹣45°＝90°，
∴S△APD+S△APB＝S△AEB+S△APB＝S△AEP+S△EPB＝AE×AP+EP×BE＝×1×1+××1＝，
∴③正确；
如图，过点B作BO⊥AE，交AE的延长线于点O，
则∠O＝90°，
∵∠BEO＝180°﹣∠AEB＝180°﹣135°＝45°，
∴△BOE是等腰直角三角形，
∴OE＝OB＝BE＝，
∴AO＝AE+OE＝1+，
在Rt△ABO中，∵AB2＝AO2+OB2＝（1+）2+（）2＝2+，
∴S正方形ABCD＝AB2＝2+；
∴④正确；
故选：A．

二．填空题（共5小题）
11．分解因式：ab2+4ab+4a＝　a（b+2）2　．
【解答】解：原式＝a（b2+4b+4）＝a（b+2）2，
故答案为：a（b+2）2．
12．公园原有一块正方形空地，后来从这块空地上划出部分区域栽种鲜花（阴影部分），原空地一边减少了3m，另一边减少了2m，剩余空地面积为56m2，设正方形空地原来的边长为xm，则可列方程为 　（x﹣3）（x﹣2）＝56　．

【解答】解：由图可得，
（x﹣3）（x﹣2）＝56，
故答案为：（x﹣3）（x﹣2）＝56．
13．已知x1，x2是一元二次方程x2+ax+b＝0的两根，且x1+x2＝3，x1x2＝1，则a，b的值分别是a＝　﹣3　，b＝　1　．
【解答】解：∵x1，x2是一元二次方程x2+ax+b＝0的两根，
∴x1+x2＝﹣a，x1x2＝b，
∵x1+x2＝3，x1x2＝1，
∴﹣a＝3，b＝1，
即a＝﹣3，b＝1．
故答案为：﹣3，1．
14．如图，在菱形ABCD中，对角线AC，BD交于点O，其中OA＝1，OB＝2，则菱形ABCD的面积为　4　．

【解答】解：∵OA＝1，OB＝2，
∴AC＝2，BD＝4，
∴菱形ABCD的面积为×2×4＝4．
故答案为：4．
15．如图所示，在平行四边形ABCD中，AB＝3，BC＝4，∠B＝60°，E是BC的中点，EF⊥AB于点F，则△DEF的面积为 　2　平方单位．

【解答】解：如图，延长DC和FE交于点G，
在平行四边形ABCD中，AB∥CD，

∴∠B＝∠ECG，
∵E为BC的中点，
∴BE＝CE＝BC＝×4＝2，
在△BEF和△CEG中，，
∴△BEF≌△CEG（ASA），
∴BF＝CG，
∵∠B＝60°，
∴∠FEB＝30°，
∴BF＝BE＝1，
∴EF＝，
∵CG＝BF＝1，CD＝AB＝3，
∴DG＝CD+CG＝3+1＝4，
∵EF⊥AB，AB∥CD，
∴DG⊥FG，
∴S△DEF＝EF•DG＝××4＝2．
故答案为：2．
三．解答题（共7小题）
16．解不等式组：．
【解答】解：，
解不等式＜1，得x＜6，
解不等式3x﹣4≤2（3x﹣2），得x≥0，
所以不等式组的解集是0≤x＜6．
17．先化简，再求值：，然后从﹣3，0，1，3中选一个合适的数作为x的值代入求值．
【解答】解：原式＝÷
＝÷
＝•
＝，
∵x（x+3）≠0，x﹣1≠0，
∴x≠0，x≠﹣3，x≠1，
∴x＝3，
∴原式＝＝．
18．解一元二次方程：
（1）4x2＝12x；（2）x2+4x+3＝0；（3）x2﹣4x﹣6＝0．
【解答】解：（1）4x2＝12x，
4x2﹣12x＝0，
4x（x﹣3）＝0，
解得x1＝0，x2＝3；
（2）x2+4x+3＝0，
（x+1）（x+3）＝0，
解得x1＝﹣1，x2＝﹣3；
（3）x2﹣4x﹣6＝0，
x2﹣4x＝6，
x2﹣4x+4＝10，
（x﹣2）2＝10，
，
∴．
19．已知关于x的一元二次方程x2﹣6x+2m﹣1＝0有x1，x2两实数根．
（1）若x1＝1，求x2及m的值；
（2）是否存在实数m，满足（x1﹣1）（x2﹣1）＝？若存在，求出实数m的值；若不存在，请说明理由．
【解答】解：（1）根据题意得，x1x2＝＝2m﹣1，x1+x2＝6，
若x1＝1，1+x2＝6，解得x2＝5，
∵5＝＝2m﹣1，
解得：x2＝5，m＝3；
（2）∵（x1﹣1）（x2﹣1）＝，
∴x1x2﹣（x1+x2）+1＝，
∵x1+x2＝6，x1x2＝2m﹣1，
∴2m﹣1﹣6+1＝，
整理得：m2﹣8m+12＝0，
解得：m1＝2，m2＝6，
经检验m1＝2，m2＝6为原方程的解，
又∵一元二次方程x2﹣6x+2m﹣1＝0有两个实数根，
∴Δ＝（﹣6）2﹣4（2m﹣1）≥0，
解得：m≤5，
∴m＝2．
20．如图，在平行四边形ABCD中，对角线AC、BD交于点O，点E为BC的中点，EF⊥CD于点F，点G为CD上一点，连接OG，OE，且OG∥EF．
（1）求证：四边形OEFG为矩形；
（2）若AD＝15，OG＝6，∠ABD＝45°，求AB的长．

【解答】（1）证明：∵四边形ABCD是平行四边形，
∴OB＝OD，
∵点E为BC的中点，
∴OE是△BCD的中位线，
∴OE∥CD，
∵OG∥EF，
∴四边形OEFG是平行四边形，
又∵EF⊥CD，
∴∠EFG＝90°，
∴平行四边形OEFG为矩形；
（2）解：∵四边形ABCD是平行四边形，
∴AB∥CD，OB＝OD，
∴∠ODG＝∠ABD＝45°，
由（1）可知，四边形OEFG为矩形，
∴∠OGF＝90°，
∴∠OGD＝90°，
∴△ODG是等腰直角三角形，
∴OD＝OG＝6，
∴BD＝2OD＝12，
如图，过D作DM⊥AB于M，
则△BDM是等腰直角三角形，
∴DM＝BM＝BD＝12，
在Rt△ADM中，由勾股定理得：AM＝＝＝9，
∴AB＝AM+BM＝9+12＝21，
即AB的长为21．

21．端午节前夕，某超市从厂家分两次购进蛋黄粽子、红豆粽子，两次进货时，两种粽子的进价不变．第一次购进蛋黄粽子60袋和红豆粽子90袋，总费用为4800元；第二次购进蛋黄粽子40袋和红豆粽子80袋，总费用为3600元．
（1）求蛋黄粽子、红豆粽子每袋的进价各是多少元？
（2）当蛋黄粽子销售价为每袋70元时，每天可售出20袋，为了促销，该超市决定对蛋黄粽子进行降价销售，经市场调研，若每袋的销售价每降低1元，则每天的销售量将增加5袋．当蛋黄粽子每袋的销售价为多少元时，每天售出蛋黄粽子所获得的利润为220元？
【解答】解：（1）设蛋黄粽子的进价是x元/袋，红豆粽子的进价是y元/袋，
根据题意得：，
解得：．
答：蛋黄粽子的进价是50元/袋，红豆粽子的进价是20元/袋；
（2）设蛋黄粽子的销售价格为m元/袋，则每袋的销售利润为（m﹣50）元，每天可售出20+5（70﹣m）＝（370﹣5m）袋，
根据题意得：（m﹣50）（370﹣5m）＝220，
解得：m2﹣124m+3744＝0，
解得：m1＝52，m2＝72（不符合题意，舍去）．
答：当蛋黄粽子每袋的销售价为52元时，每天售出蛋黄粽子所获得的利润为220元．
22．如图，在平面直角坐标系xOy中，直线AB：y＝﹣x+3与直线CD：y＝kx﹣2相交于点M（4，a），分别交坐标轴于点A，B，C，D．

（1）求a和k的值；
（2）如图，点P是直线CD上的一个动点，设点P的横坐标为m，当S△PBM＝20成立时，求点P的坐标；
（3）直线AB上有一点F，在平面直角坐标系内找一点N，使得以BF为一边，以点B，D，F，N为顶点的四边形是菱形，请直接写出符合条件的点N的坐标．
【解答】解：（1）将点M的坐标代入y＝﹣x+3并解得：a＝1，故点M（4，1），
将点M的坐标代入y＝kx﹣2，得4k﹣2＝1，解得：k＝，∴a＝1，k＝；
（2）由（1）得直线CD的表达式为：y＝x﹣2，
则点D（0，﹣2），
∴△PBM的面积＝S△BDM+S△BDP＝×BD×|xM﹣xP|＝×（3+2）|4﹣xP|＝20，
解得：xP＝﹣4或xP＝12，
故点P（﹣4，﹣5）或P（12，7）；
（3）设点F的坐标为（m，﹣m+3），点N（a，b），
由（1）知，点B、D的坐标分别为（0，3）、（0，﹣2），则BD＝5，
当BD是边时，当点F在点N的上方时，则BD＝BF，即52＝m2+（﹣m）2，
解得m＝±2，
则点F的坐标为（2，﹣+3）或（﹣2，+3）
点N在点F的正下方5个单位，
则点N（2，﹣﹣2）或（﹣2，﹣2）；
当点F在点N的下方时，则BD＝DF，
即52＝m2+（﹣m+3+2）2，解得m＝0（舍去）或4，
同理可得，点N（4，6）；
综上，点N的坐标为（2，﹣﹣2）或（﹣2，﹣2）或（4，6）．