

2023-2024学年湖南省常德市安乡县九年级(上)第一次质检数学试卷(含解析)
展开
这是一份2023-2024学年湖南省常德市安乡县九年级(上)第一次质检数学试卷(含解析),共18页。试卷主要包含了选择题,填空题等内容,欢迎下载使用。
2023-2024学年湖南省常德市安乡县九年级第一学期第一次质检数学试卷
一、选择题(共有8小题,每小题3分,共24分.)
1.﹣3的绝对值是( )
A.3 B. C. D.﹣3
2.下列等式是一元二次方程的为( )
①x2﹣2x+1=0;
②2t2=t﹣4;
③px2﹣5x=6+x(px+1);
④.
A.① B.①② C.①②③ D.①②③④
3.方程2x2﹣5x=8的二次项系数和常数项分别为( )
A.2x2和8 B.2x2和﹣8 C.2和﹣8 D.2和8
4.如图,直线l1∥l2,∠1=30°,∠2=85°,则∠3等于( )
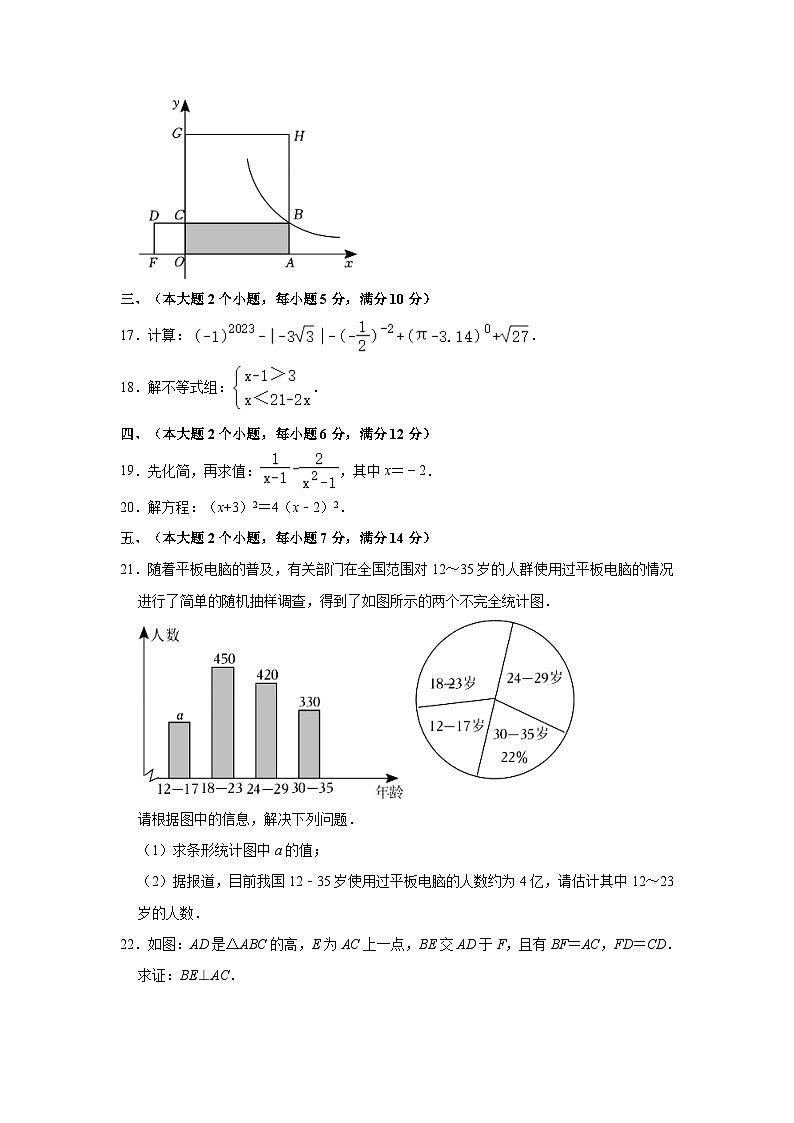
A.45° B.55° C.65° D.75°
5.下列函数中,是反比例函数的是( )
A.y=2x+1 B.y= C.y= D.y=
6.下列命题正确的是( )
A.等腰三角形是轴对称图形
B.直角三角形是中心对称图形
C.平行四边形的对角线互相垂直
D.一组邻边相等的四边形是菱形
7.安乡子龙汽车站与常德市柳叶湖汽车站相距约63.1km,则汽车由子龙汽车站行驶到柳叶湖汽车站所用时间y(小时)与行驶速度x(千米/时)之间的函数图象大致是( )
A. B.
C. D.
8.定义:如果两个一元二次方程有且只有一个相同的实数根,我们就称这两个方程为“友好方程”.如果关于x的一元二次方程x2﹣2x=0与x2+2x+m+1=0为“友好方程”,则m的值为( )
A.﹣1 B.﹣9 C.1或﹣9 D.﹣1或﹣9
二、填空题(本大题8个小题,每小题3分,满分24分)
9.计算:×= .
10.用配方法解方程x2﹣6x+1=0,则方程可配方为 .
11.要使二次根式有意义,则x应满足的条件是 .
12.国家统计局发布的2022年,中国国内国民生产总值约为121万亿,用科学记数法表示为 .
13.已知a是方程x2﹣3x﹣1011=0的一个根,则代数式2a2﹣6a+1的值是 .
14.若k的取值范围如图所示,则在反比例函数的图象的每一个分支上,y随x的增大而 .
15.对于实数a,b,我们定义一种新的运算#,规定:a#b=a2﹣b,若关于x的方程(x﹣1)#(3k)=0的一个实数根为4,则k= .
16.如图,点B是反比例函数上一点,矩形OABC的周长是16,正方形BCGH和正方形OCDF的面积之和为56,则反比例函数的解析式是 .
三、(本大题2个小题,每小题5分,满分10分)
17.计算:.
18.解不等式组:.
四、(本大题2个小题,每小题6分,满分12分)
19.先化简,再求值:,其中x=﹣2.
20.解方程:(x+3)2=4(x﹣2)2.
五、(本大题2个小题,每小题7分,满分14分)
21.随着平板电脑的普及,有关部门在全国范围对12~35岁的人群使用过平板电脑的情况进行了简单的随机抽样调查,得到了如图所示的两个不完全统计图.
请根据图中的信息,解决下列问题.
(1)求条形统计图中a的值;
(2)据报道,目前我国12﹣35岁使用过平板电脑的人数约为4亿,请估计其中12~23岁的人数.
22.如图:AD是△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD.求证:BE⊥AC.
六、(本大题2个小题,每小题8分,满分16分)
23.如图,一次函数y=mx+n(m≠0)的图象与反比例函数y=(k≠0)的图象交于第二、四象限的点A(﹣2,a)和点B(b,﹣1),过A点作x轴的垂线,垂足为点C,△AOC的面积为4.
(1)分别求出a和b的值;
(2)结合图象直接写出mx+n>中x的取值范围.
24.已知关于x的一元二次方程x2﹣2kx+k2+k﹣1=0有两个不相等的实数根.
(1)求实数k的取值范围;
(2)设方程两个实数根分别为x1,x2,且满足(x1+x2)2﹣x1•x2=5,求k的值.
七、(本大题2个小题,每小题10分,满分20分)
25.直播购物逐渐走进了人们的生活,某电商在某APP上对一款成本价为每件8元的小商品进行直播销售.如果按每件10元销售,每天可卖出200件.通过市场调查发现,每件小商品的售价每上涨1元,每天的销售件数就减少20件.将每件小商品的售价定为x(元),每天销售量y(件).
(1)求y(件)与x(元)之间的函数表达式;
(2)若电商按每件小商品的销售单价不低于成本价,且不高于15元的价格销售,要使销售该商品每天获得的利润为640元,求每件小商品的销售价应为多少元?
26.如图,平面直角坐标系xOy中,▱OABC的边OC在x轴上,对角线AC,OB交于点M,反比例函数y=(x>0)的图象经过点A(3,5)和点M.
(1)求k的值和点M的坐标;
(2)若坐标轴上有一点P,满足△OCP的面积是▱OABC的面积的2倍,求点P的坐标.
参考答案
一、选择题(本大题共有8小题,每小题3分,共24分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置上)
1.﹣3的绝对值是( )
A.3 B. C. D.﹣3
【分析】根据一个负数的绝对值是它的相反数即可求解.
解:﹣3的绝对值是3.
故选:A.
【点评】本题考查了绝对值,如果用字母a表示有理数,则数a 的绝对值要由字母a本身的取值来确定:①当a是正数时,a的绝对值是它本身a;②当a是负数时,a的绝对值是它的相反数﹣a;③当a是零时,a的绝对值是零.
2.下列等式是一元二次方程的为( )
①x2﹣2x+1=0;
②2t2=t﹣4;
③px2﹣5x=6+x(px+1);
④.
A.① B.①② C.①②③ D.①②③④
【分析】根据一元二次方程的定义:形如ax2+bx+c=0(a,b,c为常数且a≠0)的方程是一元二次方程,逐一判断即可解答.
解:①x2﹣2x+1=0,是一元二次方程;
②2t2=t﹣4,是一元二次方程;
③px2﹣5x=6+x(px+1),是一元一次方程;
④,不是一元二次方程;
所以,上列等式是一元二次方程的为①②,
故选:B.
【点评】本题考查了一元二次方程的定义,熟练掌握一元二次方程的定义是解题的关键.
3.方程2x2﹣5x=8的二次项系数和常数项分别为( )
A.2x2和8 B.2x2和﹣8 C.2和﹣8 D.2和8
【分析】根据一元二次方程的一般形式:形如ax2+bx+c=0(a,b,c为常数且a≠0),即可解答.
解:2x2﹣5x=8,
整理得:2x2﹣5x﹣8=0,
∴方程2x2﹣5x=8的二次项系数和常数项分别为2和﹣8,
故选:C.
【点评】本题考查了一元二次方程的一般形式,熟练掌握一元二次方程的一般形式是解题的关键.
4.如图,直线l1∥l2,∠1=30°,∠2=85°,则∠3等于( )
A.45° B.55° C.65° D.75°
【分析】根据平行线的性质和三角形内角和,可以求得∠3的度数.
解:∵l1∥l2,∠1=30°,
∴∠1=∠4=30°,
∵∠2=85°,∠2=∠5,
∴∠5=85°,
∵∠3+∠4+∠5=180°,
∴∠3=180°﹣∠4﹣∠5=180°﹣30°﹣85°=65°,
故选:C.
【点评】本题考查平行线的性质,解答本题的关键是明确题意,利用数形结合的思想解答.
5.下列函数中,是反比例函数的是( )
A.y=2x+1 B.y= C.y= D.y=
【分析】直接利用一次函数与反比例函数的定义分析得出答案.
解:A、y=2x+1,是一次函数,故此选项错误;
B、y=,y是x+1的反比例函数,故此选项错误;
C、y=,是反比例函数,故此选项正确;
D、y=,是正比例函数,故此选项错误;
故选:C.
【点评】此题主要考查了反比例函数与一次函数的定义,正确掌握定义是解题关键.
6.下列命题正确的是( )
A.等腰三角形是轴对称图形
B.直角三角形是中心对称图形
C.平行四边形的对角线互相垂直
D.一组邻边相等的四边形是菱形
【分析】根据轴对称图形,中心对称图形的概念,平行四边形,菱形的判定逐项判断.
解:等腰三角形是轴对称图形,故A正确,符合题意;
直角三角形不一定是中心对称图形,故B不正确,不符合题意;
平行四边形的对角线互相平分,故C不正确,不符合题意;
一组邻边相等的平行四边形是菱形,故D不正确,不符合题意;
故选:A.
【点评】本题考查命题与定理,解题的关键是掌握轴对称图形,中心对称图形的概念及平行四边形,菱形的判定.
7.安乡子龙汽车站与常德市柳叶湖汽车站相距约63.1km,则汽车由子龙汽车站行驶到柳叶湖汽车站所用时间y(小时)与行驶速度x(千米/时)之间的函数图象大致是( )
A. B.
C. D.
【分析】由y=且x>0,得双曲线为第一象限的一支即可.
解:由y=且x>0,
得双曲线为第一象限的一支;
故选:B.
【点评】本题主要考查列函数关系式以及反比例函数的图象,解题关键是注意函数自变量的范围.
8.定义:如果两个一元二次方程有且只有一个相同的实数根,我们就称这两个方程为“友好方程”.如果关于x的一元二次方程x2﹣2x=0与x2+2x+m+1=0为“友好方程”,则m的值为( )
A.﹣1 B.﹣9 C.1或﹣9 D.﹣1或﹣9
【分析】先利用因式分解法求出x2﹣2x=0的根,然后分别代入x2+2x+m+1=0,求出m的值即可.
解:x2﹣2x=0,
x(x﹣2)=0,
x1=0,x2=2,
把x1=0代入x2+2x+m+1=0得:m=﹣1,
把x2=2代入x2+2x+m+1=0得:m=﹣9,
∴m的值为﹣1或﹣9,
故选:D.
【点评】本题主要考查了一元二次方程的解,解题关键是熟练掌握一元二次方程解的定义.
二、填空题(本大题8个小题,每小题3分,满分24分)
9.计算:×= 6 .
【分析】根据二次根式的乘法法则,进行计算即可解答.
解:×=
=
=6,
故答案为:6.
【点评】本题考查了二次根式的乘除法,熟练掌握二次根式的乘法法则是解题的关键.
10.用配方法解方程x2﹣6x+1=0,则方程可配方为 (x﹣3)2=8 .
【分析】将常数项移到方程的右边,两边都加上一次项系数一半的平方配成完全平方式后即可得出答案.
解:∵x2﹣6x+1=0,
∴x2﹣6x=﹣1,
则x2﹣6x+9=﹣1+9,即(x﹣3)2=8,
故答案为:(x﹣3)2=8.
【点评】本题主要考查解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.
11.要使二次根式有意义,则x应满足的条件是 x>4 .
【分析】根据二次根式的被开方数是非负数、分母不为零列出不等式,解不等式得到答案.
解:由题意得:x﹣4>0,
解得:x>4,
故答案为:x>4.
【点评】本题考查的是二次根式有意义的条件,熟记二次根式的被开方数是非负数、分母不为零是解题的关键.
12.国家统计局发布的2022年,中国国内国民生产总值约为121万亿,用科学记数法表示为 1.21×1014 .
【分析】将一个数表示成a×10n的形式,其中1≤|a|<10,n为整数,这种记数方法叫做科学记数法,据此即可求得答案.
解:121万亿=121000000000000=1.21×1014,
故答案为:1.21×1014.
【点评】本题考查科学记数法表示较大的数,熟练掌握其定义是解题的关键.
13.已知a是方程x2﹣3x﹣1011=0的一个根,则代数式2a2﹣6a+1的值是 2023 .
【分析】先根据已知条件,求出代数式a2﹣3a的值,然后再把所求的代数式的前两项提取公因数2,再整体代入计算即可.
解:∵a是方程x2﹣3x﹣1011=0的一个根,
∴a2﹣3a﹣1011=0,
a2﹣3a=1011,
∴2a2﹣6a+1
=2(a2﹣3a)+1
=2×1011+1
=2022+1
=2023,
故答案为:2023.
【点评】本题主要考查了一元二次方程的解.解题关键是熟练掌握一元二次方程解的定义.
14.若k的取值范围如图所示,则在反比例函数的图象的每一个分支上,y随x的增大而 增大 .
【分析】由图得k<2,即k<5,得k﹣5<0,故反比例函数的图象在二四象限,故反比例函数的图象的每一个分支上,y随x的增大而增大.
解:由图得k<2,即k<5,
得k﹣5<0,
故反比例函数的图象在二四象限,
故反比例函数的图象的每一个分支上,y随x的增大而增大.
故答案为:增大.
【点评】本题主要考查反比例函数的图象双曲线的增减性,解题关键是注意每一个分支上.
15.对于实数a,b,我们定义一种新的运算#,规定:a#b=a2﹣b,若关于x的方程(x﹣1)#(3k)=0的一个实数根为4,则k= 3 .
【分析】先关键新的运算法则列出方程,然后根据方程的解的定义代入即可求出k的值.
解:由题意得,(x﹣1)2﹣3k=0,
∵其一个实数根为4,
∴(4﹣1)2﹣3k=0,
解得k=3,
故答案为:3.
【点评】本题考查了实数的运算,一元一次方程的解的定义,根据题意列出方程,熟练掌握方程的解的定义是解题的关键.
16.如图,点B是反比例函数上一点,矩形OABC的周长是16,正方形BCGH和正方形OCDF的面积之和为56,则反比例函数的解析式是 (x>0) .
【分析】首先设点B的坐标为(a,b),依题意得a>0,b>0,OA=a,OC=b,然后根据矩形OABC的周长是16得a+b=8,根据正方形BCGH和正方形OCDF的面积之和为56得a2+b2=56,据此可求出ab=4,进而可得反比例函数的解析式.
解:设点B的坐标为(a,b),
∵点B是反比例函数上一点,
∴a>0,b>0,
∴OA=a,OC=b,
∵矩形OABC的周长是16,
∴2(a+b)=16,
即:a+b=8,
又∵正方形BCGH和正方形OCDF的面积之和为56,
∴a2+b2=56,
由a+b=8,得:(a+b)2=64,
即:a2+b2+2ab=64,
将a2+b2=56代入上式,得:ab=4,
∴k=ab=4,
∴反比例函数的解析式为:(x>0).
【点评】此题主要考查了待定系数法求函数的解析式,理解题意,设出点B的坐标,并用点B的坐标分别表示出矩形OABC的周长以及正方形BCGH和正方形OCDF的面积之和是解答此题的关键.
三、(本大题2个小题,每小题5分,满分10分)
17.计算:.
【分析】根据实数的运算法则计算即可.
解:原式=﹣4+1+
=﹣4.
【点评】本题考查了实数的运算,熟练掌握零指数幂的运算法则、负整数指数幂的运算法则、绝对值的定义、有理数的乘方、算术平方根的定义是解题的关键.
18.解不等式组:.
【分析】按照解一元一次不等式组的步骤进行计算,即可解答.
解:,
解不等式①得:x>4,
解不等式②得:x<7,
∴原不等式组的解集为:4<x<7.
【点评】本题考查了解一元一次不等式组,熟练掌握解一元一次不等式组的步骤是解题的关键.
四、(本大题2个小题,每小题6分,满分12分)
19.先化简,再求值:,其中x=﹣2.
【分析】先通分,然后进行四则运算,最后将x=﹣2代入计算即可.
解:原式=,
当x=﹣2时,原式==﹣1.
【点评】解答此题的关键是把分式化到最简,然后代值计算.
20.解方程:(x+3)2=4(x﹣2)2.
【分析】利用直接开平方得两个关于x的一元一次方程,求解一元一次方程即可.
解:(x+3)2=4(x﹣2)2,
两边开平方,得x+3=±2(x﹣2),
∴x+3=2(x﹣2)或x+3=﹣2(x﹣2).
∴x+3=2x﹣4或x+3=﹣2x+4.
∴x=7或x=.
所以原方程的解为:.
【点评】本题考查了解一元二次方程,掌握直接开平方法是解决本题的关键.
五、(本大题2个小题,每小题7分,满分14分)
21.随着平板电脑的普及,有关部门在全国范围对12~35岁的人群使用过平板电脑的情况进行了简单的随机抽样调查,得到了如图所示的两个不完全统计图.
请根据图中的信息,解决下列问题.
(1)求条形统计图中a的值;
(2)据报道,目前我国12﹣35岁使用过平板电脑的人数约为4亿,请估计其中12~23岁的人数.
【分析】(1)由30﹣35岁人数及其所占百分比求出总人数,继而可得a的值;
(2)先求出12﹣23岁人数所占百分比,再乘以总人数即可得出答案.
解:(1)∵被调查的总人数为330÷22%=1500 (人),
∴a=1500﹣450﹣420﹣330=300 (人);
(2)×100%=50%,
4亿×50%=2亿.
答:估计其中12~23岁的人数为2亿.
【点评】本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
22.如图:AD是△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD.求证:BE⊥AC.
【分析】由题中条件可得Rt△BDF≌Rt△ADC,得出对应角相等,再通过角之间的转化,进而可得出结论.
【解答】证明:∵AD⊥BC,
∴∠ADC=∠BDF=90°,
∵BF=AC,FD=CD,
∴Rt△BDF≌Rt△ADC(HL),
∴∠C=∠BFD,
∵∠DBF+∠BFD=90°,
∴∠C+∠DBF=90°,
∵∠C+∠DBF+∠BEC=180°
∴∠BEC=90°,即BE⊥AC.
【点评】本题主要考查了全等三角形的判定及性质,能够熟练运用其性质求解一些简单的计算、证明问题.
六、(本大题2个小题,每小题8分,满分16分)
23.如图,一次函数y=mx+n(m≠0)的图象与反比例函数y=(k≠0)的图象交于第二、四象限的点A(﹣2,a)和点B(b,﹣1),过A点作x轴的垂线,垂足为点C,△AOC的面积为4.
(1)分别求出a和b的值;
(2)结合图象直接写出mx+n>中x的取值范围.
【分析】(1)根据△AOC的面积为4和反比例函数图象的位置,可以确定k的值,进而确定反比例函数的关系式,代入可求出点A、B的坐标,求出a、b的值;
(2)根据图象直接写出mx+n>的解集.
解:(1)∵△AOC的面积为4,
∴|k|=4,
解得,k=﹣8或k=8(正值不符合题意舍去),
∴反比例函数的关系式为y=﹣,
把点A(﹣2,a)和点B(b,﹣1)代入y=﹣得,a=﹣=4,b=﹣=8;
∴a=4,b=8;
(2)根据一次函数与反比例函数的图象可知,不等式mx+n>的解集为x<﹣2或0<x<8.
【点评】本题考查反比例函数和一次函数的交点问题,三角形的面积、待定系数法求反比例函数、一次函数的解析式,求得交点坐标是解题的关键.
24.已知关于x的一元二次方程x2﹣2kx+k2+k﹣1=0有两个不相等的实数根.
(1)求实数k的取值范围;
(2)设方程两个实数根分别为x1,x2,且满足(x1+x2)2﹣x1•x2=5,求k的值.
【分析】(1)由方程根的情况,根据根的判别式可得到关于k的不等式,则可求得k的取值范围;
(2)利用根与系数的关系,用k表示出x1+x2和x1•x2的值,由条件可得到关于k的方程,则可求得k的值.
解:(1)∵方程有两个不相等的实数根,
∴Δ>0,即(2k)2﹣4×1(k2+k﹣1)>0,
解得k<1;
(2)由根与系数的关系可得x1+x2=2k,x1•x2=k2+k﹣1,
由题意可得(2k)2﹣(k2+k﹣1)=5,
解得k=﹣1或,
∵k<1,
∴k=﹣1.
【点评】本题有要考查根的判别式,熟练掌握一元二次方程根的个数与根的判别式的关系是解题的关键.
七、(本大题2个小题,每小题10分,满分20分)
25.直播购物逐渐走进了人们的生活,某电商在某APP上对一款成本价为每件8元的小商品进行直播销售.如果按每件10元销售,每天可卖出200件.通过市场调查发现,每件小商品的售价每上涨1元,每天的销售件数就减少20件.将每件小商品的售价定为x(元),每天销售量y(件).
(1)求y(件)与x(元)之间的函数表达式;
(2)若电商按每件小商品的销售单价不低于成本价,且不高于15元的价格销售,要使销售该商品每天获得的利润为640元,求每件小商品的销售价应为多少元?
【分析】(1)由每件小商品的售价每上涨1元,每天的销售件数就减少20件,即可求解;
(2)由利润=每件商品利润×数量,列出方程可求解.
解:(1)设y与x之间的函数表达式为y=200﹣20(x﹣10)=﹣20x+400,
∴y与x之间的函数表达式为 y=﹣20x+400;
(2)由题意可得:(400﹣20x)(x﹣8)=640,
整理,得 x2﹣28x+192=0,
解得:x1=12,x2=16.
又每件小商品的销售单价不低于成本价,且不高于15元的价格,
所以 x=12,
答:将每件小商品的售价定为12元时,才能使每天的利润为640元.
【点评】本题考查了一元二次方程的应用,找到正确的数量关系是解题的关键.
26.如图,平面直角坐标系xOy中,▱OABC的边OC在x轴上,对角线AC,OB交于点M,反比例函数y=(x>0)的图象经过点A(3,5)和点M.
(1)求k的值和点M的坐标;
(2)若坐标轴上有一点P,满足△OCP的面积是▱OABC的面积的2倍,求点P的坐标.
【分析】(1)利用待定系数法求出k,再利用平行四边形的性质,推出AM=CM,推出点M的纵坐标为2.5.
(2)求出点C的坐标,即可求得▱OABC的面积,然后根据三角形面积公式求得OP的长即可解决问题.
解:(1)∵反比例函数y=(x>0)的图象经过点A(3,5),
∴k=3×5=15,
∵四边形OABC是平行四边形,
∴AM=MC,
∴点M的纵坐标为2.5,
∵点M在y=的图象上,
∴M(6,2.5).
(2)∵AM=MC,A(3,5),M(6,2.5),
∴C(9,0),
∴S▱OABC=9×5=45,
∵△OCP的面积是▱OABC的面积的2倍,
∴S△OCP=OC•OP=90,即9•OP=90,
∴OP=20,
∴P(0,20)或(0,﹣20).
【点评】本题考查反比例函数图象上的点的坐标特征,平行四边形的性质以及三角形面积等,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
相关试卷
这是一份2023-2024学年湖南省常德市安乡县八年级(上)期末数学试卷(含解析),共16页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份湖南省常德市安乡县2023-2024学年九年级上学期期末数学试题(含解析),共26页。试卷主要包含了5 毫米黑色墨水签字等内容,欢迎下载使用。
这是一份湖南省常德市安乡县2023--2024学年上学期九年级第一次质量监测考试数学试卷,文件包含湖南省常德市安乡县2023年下学期九年级第一次质量监测考试数学试卷pdf、湖南省常德市安乡县2023年下学期九年级第一次质量监测考试数学答案pdf等2份试卷配套教学资源,其中试卷共7页, 欢迎下载使用。









