2023-—2024学年北师大版数学九年级上册期中复习小卷+

这是一份2023-—2024学年北师大版数学九年级上册期中复习小卷+，文件包含2023-2024学年度第一学期九年级数学期中复习小卷及解答docx、2023-2024学年度第一学期九年级数学期中复习小卷docx等2份试卷配套教学资源，其中试卷共18页， 欢迎下载使用。
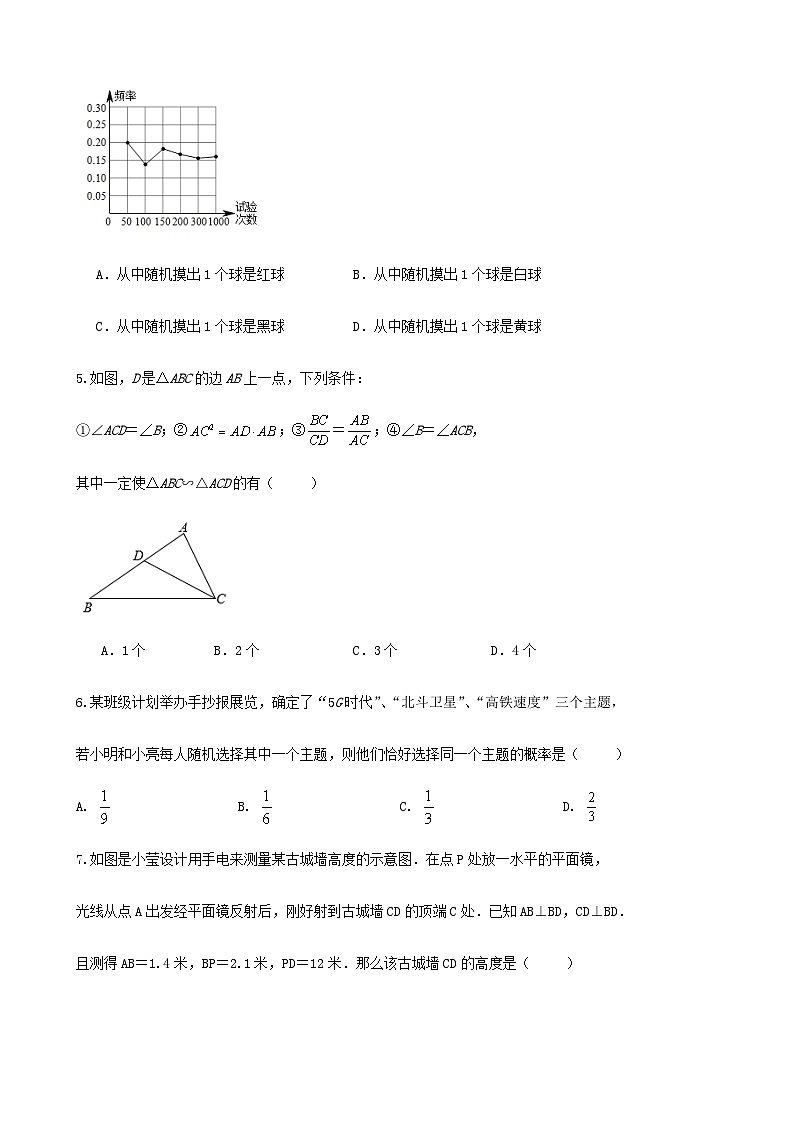
            2023-2024学年度第一学期九年级数学期中复习小卷及解答一、选择题（本大题共有10个小题，每小题3分，共30分）1．如图，AD∥BE∥CF，AB=3，AC=9，DE=2，则EF的值为（   ）A．2 B．3 C．4 D．5【答案】C2.如图，身高为1.6m的吴格霆想测量学校旗杆的高度，当她站在C处时，她头顶端的影子正好与旗杆顶端的影子重合，并测得AC＝2.0m，BC＝8.0m，则旗杆的高度是（   ）A．6m B．7m C．8m D．9m【答案】C3．一元二次方程的根的情况是（   ）A．有两个不相等的实数根 B．有两个相等的实数根C．只有一个实数根 D．没有实数根【答案】D4.某数学兴趣小组做“用频率估计概率”的试验时，在不透明的口袋中放有6个除颜色外均相同的小球，其中有3个红球，2个白球和1个黑球．用折线统计图统计了某一结果出现的频率，则符合这一结果的试验最有可能是（   ）A．从中随机摸出1个球是红球 B．从中随机摸出1个球是白球C．从中随机摸出1个球是黑球 D．从中随机摸出1个球是黄球【答案】C5.如图，D是△ABC的边AB上一点，下列条件：①∠ACD＝∠B；②；③＝；④∠B＝∠ACB，其中一定使△ABC∽△ACD的有（   ）A．1个 B．2个 C．3个 D．4个【答案】B6.某班级计划举办手抄报展览，确定了“5G时代”、“北斗卫星”、“高铁速度”三个主题，若小明和小亮每人随机选择其中一个主题，则他们恰好选择同一个主题的概率是（   ）A.  B.  C.  D. 【答案】C7.如图是小莹设计用手电来测量某古城墙高度的示意图．在点P处放一水平的平面镜，光线从点A出发经平面镜反射后，刚好射到古城墙CD的顶端C处．已知AB⊥BD，CD⊥BD．且测得AB＝1.4米，BP＝2.1米，PD＝12米．那么该古城墙CD的高度是（   ）A．6米；  B．8米；   C．10米；   D．12米．【答案】B 8．反比例函数与一次函数在同一坐标系的图象可能是（   ）A．   B．   C． D．【答案】B10．如图，路灯距地面米，身高米的小明从距离灯底（点）米的点处，沿所在直线行走米到达点时，小明身影长度（   ）A．变长2.5米 B．变短2米 C．变短2.5米 D．变短3米【答案】D二、填空题（本大题共有5个小题，每小题4分，共20分）11．已知一口袋中放有红、白、黑三种颜色的球共个，它们除颜色外其他都一样，一位同学通过多次试验后发现摸到红、白色的频率基本稳定是和，则袋中黑球的个数可能是__________【答案】2012．关于x的一元二次方程（k－1）x2－2x+1=0有两个不相等的实数根，则实数k的取值范围是       ．【答案】k＜2且k≠1 13．若点、、在反比例函数的图像上，则下列结论正确的是_______【答案】15.如图，∠ACB＝∠ADC＝90°，AC＝，AD＝2 . 当AB＝        时，△ABC∽△ACD．【答案】315．如图，在平面直角坐标系中，点在函数的图象上，点在函数图象上，若，，则的值为        ．       【答案】2三、解答题（本大题共有5个小题，共50分）16．解下列方程    (1)    (2)解：（1）所以；（2）或所以 17．如图，中，，，，，求的长度       解：∵，∴，∴，∴，即，∴，解得，  如图，在路灯下，小明的身高如图中线段AB所示，他在地面上的影子如图中线段AC所示，小亮的身高如图中线段FG所示，路灯灯泡P在线段DE上．（1）请你确定灯泡P所在的位置，并画出小亮在灯光下形成的影子．（2）如果小明的身高AB＝1.8m，他的影子长AC＝1.5m，且他到路灯的距离AD＝2m，求灯泡P距地面的高度．       解：（1）如图，点P为灯泡所在的位置，线段FH为小亮在灯光下形成的影子．         （2），，∴，∴PD＝4.2（m）．∴灯泡的高为4.2m．19．如图，已知一次函数与反比例函数的图象交于A、B两点，其中点A的坐标为．       (1)    求一次函数与反比例函数的解析式；(2)    求点B的坐标；(3)    请根据图象直接写出不等式的解集．解：（1）把点A的坐标代入一次函数的解析式中，可得：，解得：，所以一次函数的解析式为：；把点A的坐标代入反比例函数的解析式中，可得：，所以反比例函数的解析式为：；（2）    解：把一次函数与反比例函数的解析式联立得出方程组：，解得：，所以点B的坐标为；（3）    解：∵，，当或时一次函数值的图象在反比例函数图象的上方，∴不等式的解集为或． 20 .如图，，，，．点P从点C出发，以的速度沿向点A匀速运动，同时点Q从点B出发，以的速度沿向点C匀速运动，设点P、Q运动时间为t，当一个点到达终点时，另一个点随之停止．      (1)    求经过几秒后，的面积等于？(2)    经过几秒，与相似？(3)    ①是否存在t，使得的面积等于？若存在，请求出t的值，若不存在，请说明理由；②设四边形的面积为S，请直接写出S的最大值或最小值．解：（1）由题意知，，，∵，，∴，，∵的面积等于，∴∴，即∴即经过秒后，的面积等于（2）∵，∴①当时，∴，解得：；②   当时，∴，解得：；由①②可得：当经过秒或秒与相似（4）    ①不存在，理由:假设存在t，使得的面积等于，∴∴，∴，而，∴此方程无实数根，∴不存在t，使得的面积等于②   设四边形的面积为∴∴当时，S有最小值，最小值为