2023-2024学年山东省潍坊市九年级（上）开学数学试卷（9月份）（含解析）

这是一份2023-2024学年山东省潍坊市九年级（上）开学数学试卷（9月份）（含解析），共24页。试卷主要包含了选择题，多项选择题，填空题，解答题等内容，欢迎下载使用。

1．如图，把△ABC纸片的∠A沿DE折​叠，点A落在四边形CBDE外，则∠1、∠2与∠A的关系是（ ）
A．∠1+∠2＝2∠AB．∠2﹣∠1＝2∠AC．∠2﹣∠A＝2∠1D．2∠1+2∠A＝∠2
2．已知三个数a、b、c满足，则的值是（ ）
A．B．C．D．
3．将一副三角尺（在Rt△ABC中，∠ACB＝90°，∠B＝60°，在Rt△EDF中，∠EDF＝90°，∠E＝45°）如图摆放，点D为AB的中点，DE交AC于点P，DF经过点C，将△EDF绕点D顺时针方向旋转α（0°＜α＜60°），DE′交AC于点M，DF′交BC于点N，则的值为（ ）
A．B．C．D．
4．定义一种关于整数n的“F”运算：
（1）当n是奇数时，结果为3n+5；
（2）当n是偶数时，结果是（其中k是使是奇数的正整数），并且运算重复进行．
例如：取n＝58，第一次经F运算是29，第二次经F运算是92，第三次经F运算是23，第四次经F运算是74…；若n＝9，则第2023次运算结果是（ ）
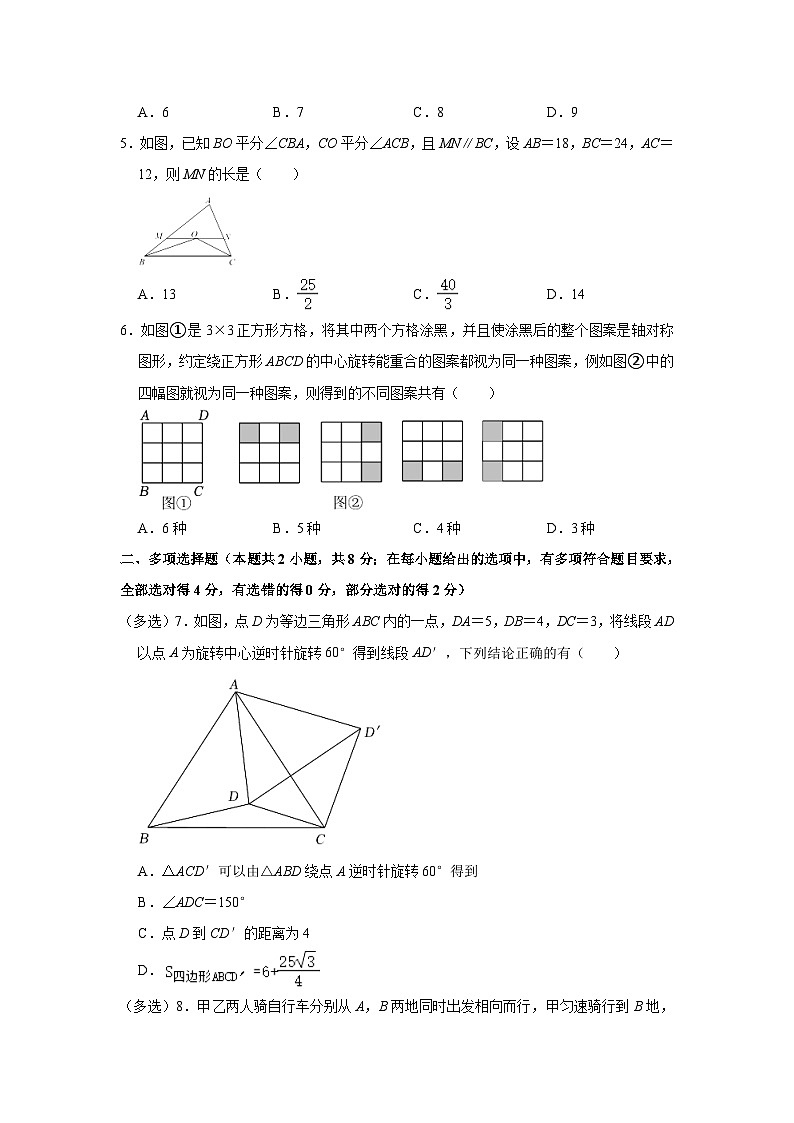
A．6B．7C．8D．9
5．如图，已知BO平分∠CBA，CO平分∠ACB，且MN∥BC，设AB＝18，BC＝24，AC＝12，则MN的长是（ ）
A．13B．C．D．14
6．如图①是3×3正方形方格，将其中两个方格涂黑，并且使涂黑后的整个图案是轴对称图形，约定绕正方形ABCD的中心旋转能重合的图案都视为同一种图案，例如图②中的四幅图就视为同一种图案，则得到的不同图案共有（ ）
A．6种B．5种C．4种D．3种
二、多项选择题（本题共2小题，共8分；在每小题给出的选项中，有多项符合题目要求，全部选对得4分，有选错的得0分，部分选对的得2分）
（多选）7．如图，点D为等边三角形ABC内的一点，DA＝5，DB＝4，DC＝3，将线段AD以点A为旋转中心逆时针旋转60°得到线段AD′，下列结论正确的有（ ）
A．△ACD′可以由△ABD绕点A逆时针旋转60°得到
B．∠ADC＝150°
C．点D到CD′的距离为4
D．
（多选）8．甲乙两人骑自行车分别从A，B两地同时出发相向而行，甲匀速骑行到B地，乙匀速骑行到A地，甲的速度大于乙的速度，两人分别到达目的地后停止骑行．两人之间的距离y（米）和骑行的时间x（秒）之间的函数关系图象如图所示，其中正确的结论有（ ）
A．a＝450
B．b＝150
C．甲的速度为8米/秒
D．当甲、乙相距50米时，甲出发了55秒或65秒
三、填空题（本题共4小题，共20分，只要求填写最后结果，每小题填对得5分.）
9．若关于x的不等式mx﹣n＞0的解集是x＜，则关于x的不等式（m+n）x＞n﹣m的解集是 ．
10．阅读材料：在求1+2+22+23+24+…+22022的值时，先设S＝1+2+22+23+24+…+22022，将等式两边同时乘以2得：2S＝2+22+23+24+25+…+22022+22023，将下式减去上式得2S﹣S＝22023﹣1，即S＝22023﹣1，求得1+2+22+23+24+…+22022＝22023﹣1，请你仿照此法计算：1+5+52+53+54+…+52023的值等于 ．
11．七巧板是我国祖先的一项卓越创造，被誉为“东方魔板”．由边长为4的正方形ABCD可以制作一副如图1所示的七巧板，现将这副七巧板在正方形EFGH内拼成如图2所示的“拼搏兔”造型（其中点Q、R分别与图2中的点E、G重合，点P在边EH上），则“拼搏兔”所在正方形EFGH的边长是 ．
12．如图是某校初中部美丽校园的一景，小明同学上学去班时要走过该段楼梯．已知本段楼梯共有10个阶梯，如果每步只允许走一个或两个阶梯，那么小明同学共有 种方法走完本段楼梯．
四、解答题（本题共4小题，共48分.解答应写出必要文字说明或演算步骤．）
13．如图①，对角线互相垂直的四边形叫做垂美四边形．
【概念理解】（1）如图②，在四边形ABCD中，AB＝AD，CB＝CD，问四边形ABCD是垂美四边形吗？请说明理由；
【性质探究】（2）如图①，四边形ABCD的对角线AC，BD交于点O，AC⊥BD．试证明：AD2+BC2＝AB2+CD2；
【解决问题】（3）如图③，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连接CE，BG，GE．已知AC＝8，AB＝10，求GE的长．
14．某学校计划今年国庆期间组织部分教师到外地进行学习，预订宾馆住宿时，有住宿条件完全一样的甲、乙两家宾馆可供选择，其收费标准均为每人每天120元，并且各自推出不同的优惠方案．
【问题信息】外出学习教师不超过100人．甲宾馆是35人以内（含35人）按标准收费，超过35人的，超出部分按九折收费；乙宾馆是45人以内（含45人）的按标准收费，超过45人的，超出部分按八折收费．
【问题设计】如果你是这个学校负责人，你会怎样选择宾馆？请你给出你的设计方案和理由．
15．数学来源于生活，生活中处处有数学，用我们平时喝的糖水做“糖水实验”也能验证发现一些数学结论．现有a克糖水，其中含有b克糖（a＞b＞0），则糖水的浓度（即糖的质量与糖水的质量比）为．
（1）糖水实验一：加入m克水，则糖水的浓度为 ．生活经验告诉我们，糖水加水后会变淡，由此可以写出一个不等式 ，我们趣称为“糖水不等式”．
（2）糖水实验二：
将“糖水实验一”中的“加入m克水”改为“加入m克糖”，则糖水的浓度为 ．根据生活经验，请你写出一个新的“糖水不等式” ．
（3）请结合（2）探究得到的结论尝试证明：
设a、b、c为△ABC三边的长，求证：．
16．综合与实践课上，老师让同学们以“矩形的折叠”为主题开展数学活动．
（1）操作判断
操作一：对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展平；
操作二：在AD上选一点P，连接BP，沿BP折叠，使点A落在矩形内部点M处，把纸片展平，连接PM，BM．
如图1，当点M在EF上时，根据以上操作，写出一个度数为30°的角为 ；
（2）迁移探究
小华将矩形纸片换成正方形纸片，继续探究，过程如下：
将正方形纸片ABCD按照（1）中的方式操作，并延长PM交CD于点Q，连接BQ．
①如图2，当点M在EF上时，则∠MBQ＝ ；
②改变点P在AD上的位置（点P不与点A，D重合）如图3，判断∠MBQ 与∠CBQ 的数量关系，并说明理由；
（3）拓展应用
在（2）的探究中，已知正方形纸片ABCD的边长为8cm，当FQ＝1cm 时，请直接写出AP的长．
参考答案
一、选择题（本题共6小题，共24分；在每小题给出的四个选项中，只有一个是正确的，请把正确的选项选出来，每小题选对得4分，多选、不选、错选记0分.）
1．如图，把△ABC纸片的∠A沿DE折​叠，点A落在四边形CBDE外，则∠1、∠2与∠A的关系是（ ）
A．∠1+∠2＝2∠AB．∠2﹣∠1＝2∠AC．∠2﹣∠A＝2∠1D．2∠1+2∠A＝∠2
【分析】分别延长CE、BD交于A′点，连接AA′，由三角形外角的性质得出∠2＝∠EA′A+∠EAA′，∠1＝∠DA′A+∠DAA′，再由翻折的性质得EA＝EA′，DA＝DA′，则∠EA′A＝∠EAA′，∠DA′A＝∠DAA′，即可得出答案．
解：如图，分别延长CE、BD交于A′点，连接AA′，
∴∠2＝∠EA′A+∠EAA′，∠1＝∠DA′A+∠DAA′，
由翻折的性质得：EA＝EA′，DA＝DA′，
∴∠EA′A＝∠EAA′，∠DA′A＝∠DAA′，
∴∠2﹣∠1＝2（∠EAA′﹣∠DAA′）＝2∠EAD，
故选：B．
【点评】本题考查了翻折的性质、等腰三角形的性质等知识，熟练掌握翻折的性质和等腰三角形的性质是解题的关键．
2．已知三个数a、b、c满足，则的值是（ ）
A．B．C．D．
【分析】先将条件式化简，然后根据分式的运算法则即可求出答案．
解：∵，
∴＝5，＝6，＝7，
∴＝5，+＝6，+＝7，
∴2（）＝18，
∴＝9，
∴＝，
故选：A．
【点评】本题考查分式的运算，解题的关键是找出各式之间的关系，本题属于中等题型．
3．将一副三角尺（在Rt△ABC中，∠ACB＝90°，∠B＝60°，在Rt△EDF中，∠EDF＝90°，∠E＝45°）如图摆放，点D为AB的中点，DE交AC于点P，DF经过点C，将△EDF绕点D顺时针方向旋转α（0°＜α＜60°），DE′交AC于点M，DF′交BC于点N，则的值为（ ）
A．B．C．D．
【分析】先根据直角三角形斜边上的中线性质得CD＝AD＝DB，则∠ACD＝∠A＝30°，∠BCD＝∠B＝60°，由于∠EDF＝90°，可利用互余得∠CPD＝60°，再根据旋转的性质得∠PDM＝∠CDN＝α，于是可判断△PDM∽△CDN，得到＝，然后在Rt△PCD中利用正切的定义得到tan∠PCD＝tan30°＝，于是可得＝即可得答案．
解：∵点D为斜边AB的中点，
∴CD＝AD＝DB，
∴∠ACD＝∠A＝30°，∠BCD＝∠B＝60°，
∵∠EDF＝90°，
∴∠CPD＝60°，
∴∠MPD＝∠NCD，
∵△EDF绕点D顺时针方向旋转α（0°＜α＜60°），
∴∠PDM＝∠CDN＝α，
∴△PDM∽△CDN，
∴＝，
在Rt△PCD中，∵tan∠PCD＝tan30°＝，
∴＝tan30°＝．
∴＝．
故选：D．
【点评】本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了相似三角形的判定与性质．
4．定义一种关于整数n的“F”运算：
（1）当n是奇数时，结果为3n+5；
（2）当n是偶数时，结果是（其中k是使是奇数的正整数），并且运算重复进行．
例如：取n＝58，第一次经F运算是29，第二次经F运算是92，第三次经F运算是23，第四次经F运算是74…；若n＝9，则第2023次运算结果是（ ）
A．6B．7C．8D．9
【分析】根据运算结果的变化找出变化规律，依此规律即可得到第2020次运算结果．
解：由题意n＝9时，第一次经F运算是32，第二次经F运算是1，第三次经F运算是8，第四次经F运算是1…
以后出现1、8循环，奇数次是8，偶数次是1，
∴第2023次运算结果是8，
故选：C．
【点评】本题考查了规律型中数字的变化以及有理数的混合运算，解答本题的关键是明确题意，发现运算结果的变化特点．
5．如图，已知BO平分∠CBA，CO平分∠ACB，且MN∥BC，设AB＝18，BC＝24，AC＝12，则MN的长是（ ）
A．13B．C．D．14
【分析】根据BO平分∠CBA，CO平分∠ACB，且MN∥BC，可得出MO＝MC，NO＝NB，所以三角形AMN的周长是AB+AC，再利用相似三角形的性质求出MN．
解：∵BO平分∠CBA，CO平分∠ACB，
∴∠NBO＝∠OBC，∠OCM＝∠OCB，
∵MN∥BC，
∴∠NOB＝∠OBC，∠MOC＝∠OCB，
∴∠NBO＝∠NOB，∠MOC＝∠MCO，
∴MO＝MC，NO＝NB，
∵AB＝18，AC＝12，
∴△AMN的周长＝AM+MN+AN＝AB+AC＝18+12＝30，
∵MN∥BC，
∴△AMN∽△ABC，
∴＝，
∴＝
∴MN＝，
故选：C．
【点评】本题考查了等腰三角形的判定和性质以及平行线的性质，相似三角形的判定和性质等知识，解题的关键是正确寻找相似三角形解决问题．．
6．如图①是3×3正方形方格，将其中两个方格涂黑，并且使涂黑后的整个图案是轴对称图形，约定绕正方形ABCD的中心旋转能重合的图案都视为同一种图案，例如图②中的四幅图就视为同一种图案，则得到的不同图案共有（ ）
A．6种B．5种C．4种D．3种
【分析】根据轴对称的定义及题意要求画出所有图案后即可得出答案．
解：得到的不同图案有：
共6种．
故选：A．
【点评】本题考查了利用轴对称设计图案，培养学生实际操作能力，用到了图形的旋转及轴对称的知识，需要灵活掌握．
二、多项选择题（本题共2小题，共8分；在每小题给出的选项中，有多项符合题目要求，全部选对得4分，有选错的得0分，部分选对的得2分）
（多选）7．如图，点D为等边三角形ABC内的一点，DA＝5，DB＝4，DC＝3，将线段AD以点A为旋转中心逆时针旋转60°得到线段AD′，下列结论正确的有（ ）
A．△ACD′可以由△ABD绕点A逆时针旋转60°得到
B．∠ADC＝150°
C．点D到CD′的距离为4
D．
【分析】根据旋转的性质得AD＝AD′，∠DAD′＝60°，由△ABC为等边三角形得到AB＝AC，∠BAC＝60°，则把△ABD绕点A逆时针旋转60°后，AB与AC重合，AD与AD′重合，于是可对③进行判断；再根据勾股定理的逆定理得到△DD′C为直角三角形，则可对②④进行判断；由于S四边形ADCD′＝S△ADD′+S△D′DC，利用等边三角形的面积公式和直角三角形面积公式计算后可对⑤进行判断．
解：∵线段AD以点A为旋转中心逆时针旋转60°得到线段AD′，
∴AD＝AD′，∠DAD′＝60°，
∵△ABC为等边三角形，
∴AB＝AC，∠BAC＝60°，
∴把△ABD绕点A逆时针旋转60°后，AB与AC重合，AD与AD′重合，
∴△ACD′可以由△ABD绕点A逆时针旋转60°得到，所以A正确；
∴D′C＝DB＝4，
∵DC＝3，
在△DD′C中，
∵32+42＝52，
∴DC2+D′C2＝DD′2，
∴△DD′C为直角三角形，
∴∠DCD′＝90°，
∵△ADD′为等边三角形，
∴∠ADD′＝60°，
∴∠ADC≠150°，所以B错误；
∵∠DCD′＝90°，
∴DC⊥CD′，
∴点D到CD′的距离为3，所以C错误；
∵S△ADD′+S△D′DC
＝×52+×3×4
＝6+，所以D正确．
故选：AD．
【点评】本题考查了旋转的性质：旋转前后两图形全等；对应点到旋转中心的距离相等；对应点与旋转中心的连线段的夹角等于旋转角．也考查了等边三角形的判定与性质以及勾股定理的逆定理．
（多选）8．甲乙两人骑自行车分别从A，B两地同时出发相向而行，甲匀速骑行到B地，乙匀速骑行到A地，甲的速度大于乙的速度，两人分别到达目的地后停止骑行．两人之间的距离y（米）和骑行的时间x（秒）之间的函数关系图象如图所示，其中正确的结论有（ ）
A．a＝450
B．b＝150
C．甲的速度为8米/秒
D．当甲、乙相距50米时，甲出发了55秒或65秒
【分析】根据函数图象中的数据，可以计算出甲和乙的速度，从而可以判断C；然后根据甲的速度可以计算出a的值，即可判断A；根据乙的速度，可以计算出b的值，可以判断B；根据甲和乙相遇前和相遇后相距50米，可以计算出甲出发的时间，即可判断D．
解：由图可得，甲的速度为：600÷100＝6（米/秒），故C错误，不符合题意；
∴乙的速度为：600÷60﹣6＝4（米/秒），
∴a＝4×100＝400，故A错误，不符合题意；
b＝600÷4＝150，故B正确，符合题意；
设当甲、乙相距50米时，甲出发了m秒，
两人相遇前：（600﹣50）＝m（6+4），
解得m＝55；
两人相遇后：（600+50）＝m（6+4），
解得m＝65；故D正确，符合题意；
故选：BD．
【点评】本题考查一次函数的应用，解答本题的关键是明确题意，利用数形结合的思想解答．
三、填空题（本题共4小题，共20分，只要求填写最后结果，每小题填对得5分.）
9．若关于x的不等式mx﹣n＞0的解集是x＜，则关于x的不等式（m+n）x＞n﹣m的解集是 x＜﹣ ．
【分析】根据已知求出m、n都为负数，求出m＝7n，求出m+n和n﹣m的值，即可求出答案．
解：∵关于x的不等式mx﹣n＞0的解集是x＜，
∴m＜0，＝，
∴m＝7n，
∴n＜0，
∴m+n＝8n，n﹣m＝﹣6n，
∴关于x的不等式（m+n）x＞n﹣m的解集是x＜﹣，
即x＜﹣，
故答案为：x＜﹣．
【点评】本题考查了解一元一次不等式，能求出m、n为负数和m＝7n是解此题的关键．
10．阅读材料：在求1+2+22+23+24+…+22022的值时，先设S＝1+2+22+23+24+…+22022，将等式两边同时乘以2得：2S＝2+22+23+24+25+…+22022+22023，将下式减去上式得2S﹣S＝22023﹣1，即S＝22023﹣1，求得1+2+22+23+24+…+22022＝22023﹣1，请你仿照此法计算：1+5+52+53+54+…+52023的值等于 ．
【分析】仿照题中的形式进行求解即可．
解：设S＝1+5+52+53+54+…+52023，
将等式两边同时乘以5得：5S＝5+52+53+54+…+52024，
将下式减去上式得：4S＝52024﹣1，
则S＝，
即1+5+52+53+54+…+52023＝，
故答案为：．
【点评】本题主要考查规律型：数字的变化类，有理数的混合运算，解答的关键是理解清楚题意，总结出规律．
11．七巧板是我国祖先的一项卓越创造，被誉为“东方魔板”．由边长为4的正方形ABCD可以制作一副如图1所示的七巧板，现将这副七巧板在正方形EFGH内拼成如图2所示的“拼搏兔”造型（其中点Q、R分别与图2中的点E、G重合，点P在边EH上），则“拼搏兔”所在正方形EFGH的边长是 4 ．
【分析】如图2中，连接EG，GM⊥EN交EN的延长线于M，利用勾股定理解决问题即可．
解：如图2中，连接EG，作GM⊥EN交EN的延长线于M．
在Rt△EMG中，∵GM＝4，EM＝2+2+4+4＝12，
∴EG＝＝＝4，
∴EH＝＝4，
解法二：如图，连接EG交MN于点O．
由题意，EN＝MN＝4，GM＝8，
∵∠EON＝∠GOM，∠N＝∠M＝90°，
∴△EON∽△GOM，
∴＝＝，
∴ON＝MN＝，
∴OE＝＝，OG＝2OE＝，
∴GF＝EG＝（OE+OG）＝4．
故答案为4．
【点评】本题考查正方形的性质，七巧板，勾股定理等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题．
12．如图是某校初中部美丽校园的一景，小明同学上学去班时要走过该段楼梯．已知本段楼梯共有10个阶梯，如果每步只允许走一个或两个阶梯，那么小明同学共有 89 种方法走完本段楼梯．
【分析】第i个台阶可以在第（i﹣1）个台阶的基础上，上一个台阶，也可以在第（i﹣2）个台阶基础上，上2个台阶，所以一共有i个台阶的方法数等于一共有（i﹣1）个台阶的方法数加上（i﹣2）个台阶的方法数，据此可得答案．
解：根据每步只允许走一个或两个阶梯，可得：
（1）当一共有1个台阶时，有1种方法；
（2）当一共有两个台阶时，有1+1＝2种方法，（即1﹣1，2）；
（3）当一共有三个台阶时，有1+2＝3种方法，（即1﹣1﹣1，1﹣2，2﹣1）；
（4）当一共有4个台阶时，有2+3＝5种方法，（即1﹣1﹣1﹣1，1﹣1﹣2，1﹣2﹣1，2﹣1﹣1，2﹣2）；
（5）当一共有5个台阶时，有3+5＝8种方法，（即1﹣1﹣1﹣1﹣1，1﹣1﹣1﹣2，1﹣1﹣2﹣1，1﹣2﹣1﹣1，1﹣2﹣2，2﹣1﹣1﹣1，2﹣1﹣2，2﹣2﹣1）；
根据规律可知：
（6）当一共有6个台阶时，有5+8＝13种方法；
（7）当一共有7个台阶时，有8+13＝21种方法；
（8）当一共有8个台阶时，有13+21＝34种方法；
（9）当一共有9个台阶时，有21+34＝55种方法；
（10）当一共有10个台阶时，有34+55＝89种方法；
故答案为：89．
【点评】本题考查了排列与组合问题，规律探索，解题的关键是从较小的数开始，找到规律．
四、解答题（本题共4小题，共48分.解答应写出必要文字说明或演算步骤．）
13．如图①，对角线互相垂直的四边形叫做垂美四边形．
【概念理解】（1）如图②，在四边形ABCD中，AB＝AD，CB＝CD，问四边形ABCD是垂美四边形吗？请说明理由；
【性质探究】（2）如图①，四边形ABCD的对角线AC，BD交于点O，AC⊥BD．试证明：AD2+BC2＝AB2+CD2；
【解决问题】（3）如图③，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连接CE，BG，GE．已知AC＝8，AB＝10，求GE的长．
【分析】（1）根据垂直平分线的判定定理证明即可；
（2）根据垂直的定义和勾股定理解答即可；
（3）根据垂美四边形的性质、勾股定理、结合（2）的结论计算．
【解答】（1）解：四边形ABCD是垂美四边形．证明如下：
∵AB＝AD，
∴点A在线段BD的垂直平分线上，
∵CB＝CD，
∴点C在线段BD的垂直平分线上，
∴直线AC是线段BD的垂直平分线，
∴AC⊥BD，即四边形ABCD是垂美四边形；
（2）证明：如图1中，
∵AC⊥BD，
∴∠AOD＝∠AOB＝∠BOC＝∠COD＝90°，
由勾股定理得，AD2+BC2＝AO2+DO2+BO2+CO2，
AB2+CD2＝AO2+BO2+CO2+DO2，
∴AD2+BC2＝AB2+CD2．
（3）解：连接CG、BE，
∵∠CAG＝∠BAE＝90°，
∴∠CAG+∠BAC＝∠BAE+∠BAC，即∠GAB＝∠CAE，
在△GAB和△CAE中，
，
∴△GAB≌△CAE（SAS），
∴∠ABG＝∠AEC，又∠AEC+∠AME＝90°，
∴∠ABG+∠AME＝90°，即CE⊥BG，
∴四边形CGEB是垂美四边形，
由（2）得，CG2+BE2＝CB2+GE2，
∵AC＝8，AB＝10，
∴BC＝6，CG＝8，BE＝10，
∴GE2＝CG2+BE2﹣CB2＝292，
∴GE＝2．
【点评】本题考查的是正方形的性质、全等三角形的判定和性质、垂直的定义、勾股定理的应用，正确理解垂美四边形的定义、灵活运用勾股定理是解题的关键．
14．某学校计划今年国庆期间组织部分教师到外地进行学习，预订宾馆住宿时，有住宿条件完全一样的甲、乙两家宾馆可供选择，其收费标准均为每人每天120元，并且各自推出不同的优惠方案．
【问题信息】外出学习教师不超过100人．甲宾馆是35人以内（含35人）按标准收费，超过35人的，超出部分按九折收费；乙宾馆是45人以内（含45人）的按标准收费，超过45人的，超出部分按八折收费．
【问题设计】如果你是这个学校负责人，你会怎样选择宾馆？请你给出你的设计方案和理由．
【分析】设共有x（x≤100）名教师到外地进行学习，当x≤35时，选择甲宾馆所需费用为120x元，选择乙宾馆所需费用为120x元，由120x＝120x，可得出此时选择两宾馆所需费用相同；当35＜x≤45时，选择甲宾馆所需费用为（108x+420）元，选择乙宾馆所需费用为120x元，由108x+420＜120x，可得出此时选择甲宾馆所需费用较少；当45＜x≤100时，选择甲宾馆所需费用为（108x+420）元，选择乙宾馆所需费用为（96x+1080）元，分108x+420＜96x+1080，108x+420＝96x+1080及108x+420＞96x+1080三种情况，求出x的值或x的取值范围．综上所述，即可找出选择方案．
解：设共有x（x≤100）名教师到外地进行学习．
当x≤35时，选择甲宾馆所需费用为120x元，选择乙宾馆所需费用为120x元，
∵120x＝120x，
∴此时选择两宾馆所需费用相同，即可以任意选择甲、乙两家宾馆；
当35＜x≤45时，选择甲宾馆所需费用为120×35+120×0.9（x﹣35）＝（108x+420）元，选择乙宾馆所需费用为120x元，
∵108x+420＜120x，
∴此时选择甲宾馆所需费用较少；
当45＜x≤100时，选择甲宾馆所需费用为120×35+120×0.9（x﹣35）＝（108x+420）元，选择乙宾馆所需费用为120×45+120×0.8（x﹣45）＝（96x+1080）元，
若108x+420＜96x+1080，则x＜55，此时选择甲宾馆所需费用较少；
若108x+420＝96x+1080，则x＝55，此时选择两宾馆所需费用相同；
若108x+420＞96x+1080，则x＞55，此时选择乙宾馆所需费用较少．
综上所述，方案设计为：当x≤35或x＝55时，选择两宾馆所需费用相同；当35＜x＜55时，选择甲宾馆更实惠；当55＜x≤100时，选择乙宾馆更实惠．
【点评】本题考查了一元一次方程的应用、列代数式以及一元一次不等式的应用，根据各数量之间的关系，用含x的代数式分别表示出选择甲、乙两家宾馆所需费用是解题的关键．
15．数学来源于生活，生活中处处有数学，用我们平时喝的糖水做“糖水实验”也能验证发现一些数学结论．现有a克糖水，其中含有b克糖（a＞b＞0），则糖水的浓度（即糖的质量与糖水的质量比）为．
（1）糖水实验一：加入m克水，则糖水的浓度为 ．生活经验告诉我们，糖水加水后会变淡，由此可以写出一个不等式 ，我们趣称为“糖水不等式”．
（2）糖水实验二：
将“糖水实验一”中的“加入m克水”改为“加入m克糖”，则糖水的浓度为 ．根据生活经验，请你写出一个新的“糖水不等式” ．
（3）请结合（2）探究得到的结论尝试证明：
设a、b、c为△ABC三边的长，求证：．
【分析】（1）①根据题意列式表示；根据“糖水加水后会变淡”可列出不等式；
（2）根据题意列出代数式和不等式即可；
（3）利用三角形的三边关系得到a+b＞c，b+c＞a，c+a＞b，即，，，在通过本题糖水不等式变形求证即可．
解：（1）①由题意得：加入m克水后，糖水的浓度为，
∵糖水加水后会变淡，
∴．
故答案为：，；
（2）由题意得：加入m克糖后，糖水的浓度为，
根据生活经验，加入m（m＞0）克糖后，糖水会变甜，
∴，
故答案为：，；
（3）在△ABC中，a+b＞c，b+c＞a，c+a＞b，且a＞0，b＞0，c＞0，
∴，，，
由糖水不等式得，，，，
∴＝2，
∴．
【点评】本题主要考查分式的运算及大小比较，理解不等式并能够利用糖水不等式以及三角形三边关系证明是解决本题的关键．
16．综合与实践课上，老师让同学们以“矩形的折叠”为主题开展数学活动．
（1）操作判断
操作一：对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展平；
操作二：在AD上选一点P，连接BP，沿BP折叠，使点A落在矩形内部点M处，把纸片展平，连接PM，BM．
如图1，当点M在EF上时，根据以上操作，写出一个度数为30°的角为 ∠BME或∠ABP或∠PBM或∠MBC ；
（2）迁移探究
小华将矩形纸片换成正方形纸片，继续探究，过程如下：
将正方形纸片ABCD按照（1）中的方式操作，并延长PM交CD于点Q，连接BQ．
①如图2，当点M在EF上时，则∠MBQ＝ 15° ；
②改变点P在AD上的位置（点P不与点A，D重合）如图3，判断∠MBQ 与∠CBQ 的数量关系，并说明理由；
（3）拓展应用
在（2）的探究中，已知正方形纸片ABCD的边长为8cm，当FQ＝1cm 时，请直接写出AP的长．
【分析】（1）根据折叠的性质，得，结合矩形的性质得∠BME＝30°，进而可得∠ABP＝∠PBM＝∠MBC＝30°；
（2）①根据折叠的性质，可证Rt△BQM≌Rt△BQC（HL），即可求解，
②根据折叠的性质，可证Rt△BQM≌Rt△BQC（HL），即可求解；
（3）由（2）可得QM＝QC，分两种情况：当点Q在点F的下方时，当点Q在点F的上方时，设AP＝PM＝xcm，分别表示出PD，DQ，PQ，由勾股定理即可求解．
解：（1）∵，
∴，
∵∠BEM＝90°，
∴∠BME＝30°，
∴∠MBE＝60°，
∵∠ABP＝∠PBM，
∴∠ABP＝∠PBM＝∠MBC＝30°；
故答案为：∠BME或∠ABP或∠PBM或∠MBC；
（2）①∵四边形ABCD是正方形，
∴AB＝BC，∠A＝∠ABC＝∠C＝90°，
由折叠性质得：AB＝BM，∠PMB＝∠BMQ＝∠A＝90°，
∴BM＝BC；
∵BQ＝BQ，
∴Rt△BQM≌Rt△BQC（HL），
∴∠MBQ＝∠CBQ，
∵∠MBC＝30°，
∴∠MBQ＝∠CBQ＝15°；
故答案为：15°；
②∠MBQ＝∠CBQ，理由如下：
∵BM＝BC，BQ＝BQ，
∴Rt△BQM≌Rt△BQC（HL），
∴∠MBQ＝∠CBQ；
（3）当点Q在点F的下方时，如图，
∵FQ＝1cm，DF＝FC＝4cm，AB＝8cm，
∴QC＝CD﹣DF﹣FQ＝8﹣4﹣1＝3（cm），DQ＝DF+FQ＝4+1＝5（cm），
由（2）可得，QM＝QC＝3（cm），
设AP＝PM＝xcm，PD＝（8﹣x）cm，
∵PD2+DQ2＝PQ2，
即（8﹣x）2+52＝（x+3）2，
解得：x＝，
∴AP＝（cm）；
当点Q在点F的上方时，如图，
∵FQ＝1cm，DF＝FC＝4cm，AB＝8cm，
∴QC＝5cm，DQ＝3cm，
由（2）可知，QM＝QC＝5cm，
设AP＝PM＝xcm，PD＝（8﹣x）cm，
∴PD2+DQ2＝PQ2，
即（8﹣x）2+32＝（x+5）2，
解得：x＝，
∴AP＝cm．
综上所述：AP为cm或cm．
【点评】本题主要考查矩形与折叠，正方形的性质、勾股定理、三角形的全等，掌握相关知识并灵活应用是解题的关键．