数学拓展模块一 上册3.1 椭圆优秀同步训练题

这是一份数学拓展模块一 上册3.1 椭圆优秀同步训练题，文件包含同步知识点高教版2021中职数学拓展模块一上册专题06椭圆-讲义原卷版docx、同步知识点高教版2021中职数学拓展模块一上册专题06椭圆-讲义解析版docx等2份试卷配套教学资源，其中试卷共22页， 欢迎下载使用。
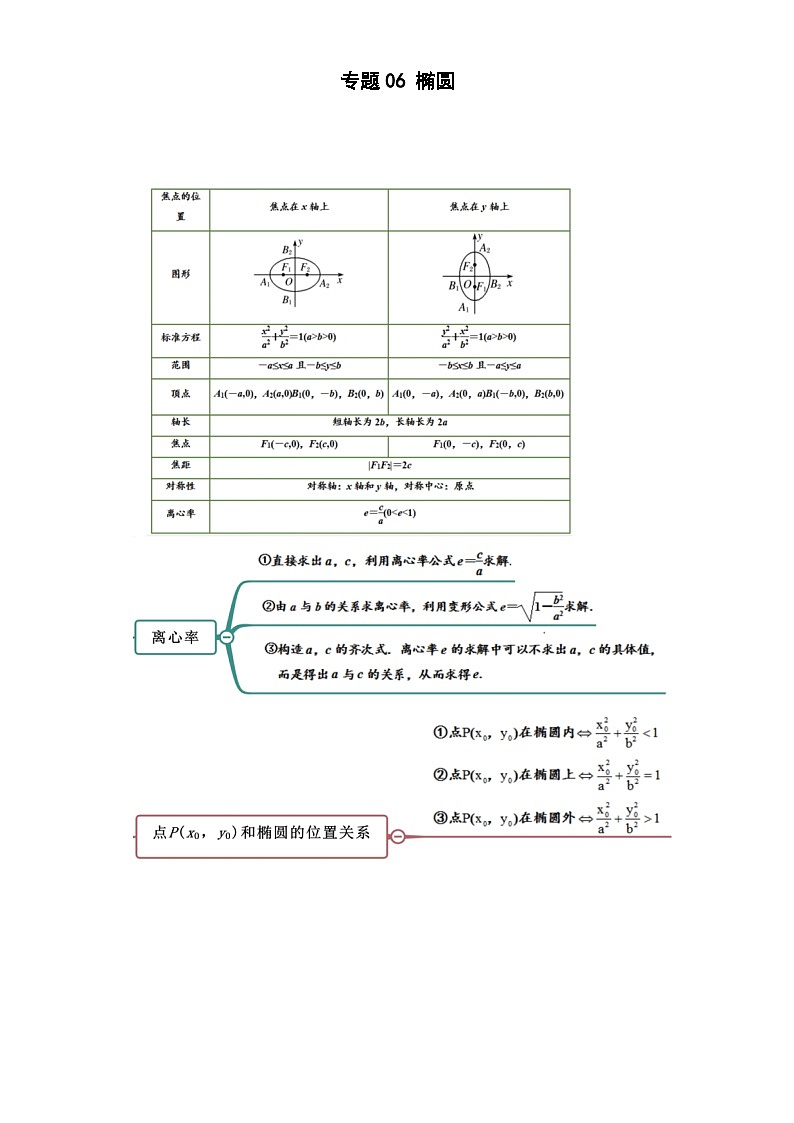
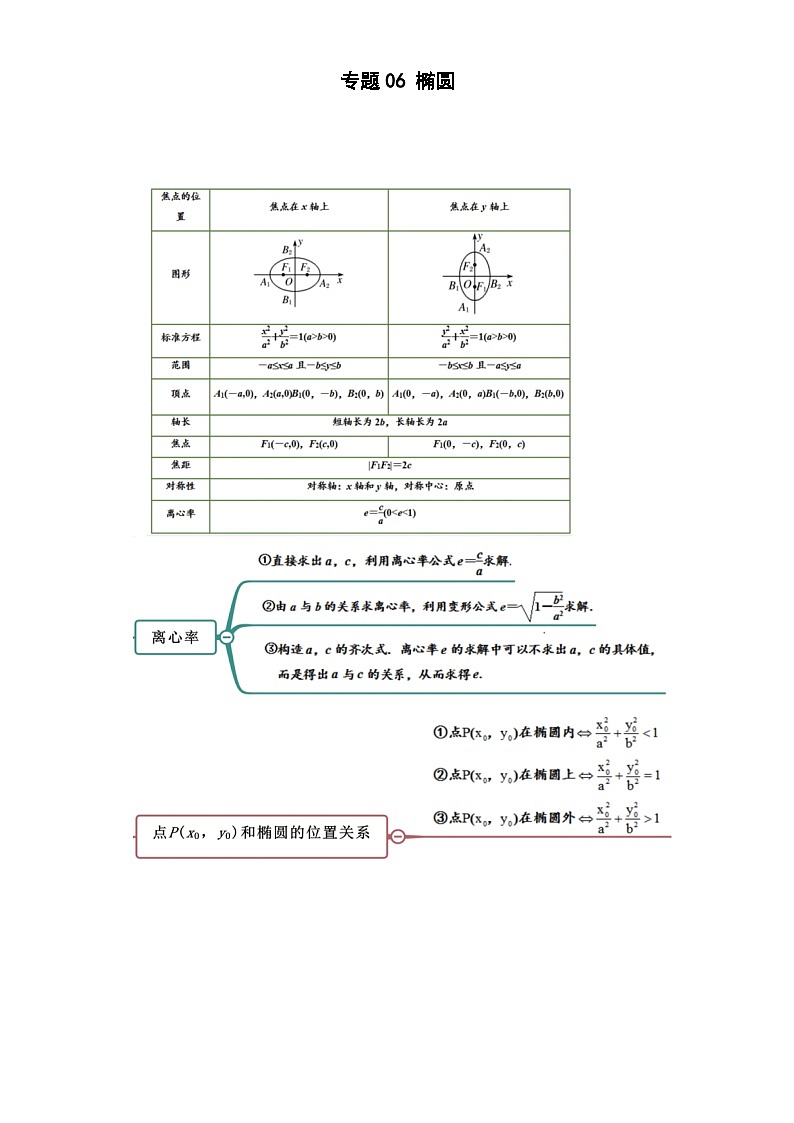
专题06 椭圆   【题型1 椭圆的定义及辨析】【题型2 利用椭圆定义求标准方程】【题型3 椭圆上的点到焦点的距离】【题型4 判断方程是否表示椭圆】【题型5 求标准方程】【题型6根据椭圆的标准方程研究其几何性质】【题型7根据椭圆的几何性质求其标准方程 】【题型8求椭圆的离心率的值】【题型9直线与椭圆的位置关系】【题型10弦长】 【题型1 椭圆的定义及辨析】1、椭圆的定义：平面内一个动点到两个定点、的距离之和等于常数，这个动点的轨迹叫椭圆. 这两个定点（,）叫椭圆的焦点，两焦点的距离（）叫作椭圆的焦距.说明：若，的轨迹为线段；若，的轨迹无图形2、定义的集合语言表述集合.         【典例1】（2023秋·四川南充·高二四川省南充高级中学校考期末）设定点，，动点P满足条件，则点P的轨迹是（    ）A．椭圆 B．线段 C．不存在 D．椭圆或线段【答案】A【详解】因为，，所以，所以，所以点P的轨迹是以，为焦点的椭圆.故选：A.【题型2 利用椭圆定义求标准方程】椭圆的标准方程焦点位置焦点在轴上焦点在轴上标准方程（）（）图象焦点坐标，，的关系【典例2】（2023·上海·高二专题练习）方程，化简的结果是（    ）A． B． C． D．【答案】B【详解】由，可得点到定点，的距离之和等于12，即，所以动点的轨迹是焦点在轴上的椭圆，设其方程为，则，，所以，，故方程为.【题型3 椭圆上的点到焦点的距离】【典例3】（2023·全国·高三专题练习）已知椭圆上一点到右准线的距离为，则点到它的左焦点的距离为（     ）A． B． C． D．【答案】A【详解】设分别为椭圆的左、右焦点，到左准线的距离为，到右准线的距离为，由圆锥曲线的统一定义知：，解得：，又，解得：，到它的左焦点距离为．故选：A.【题型4 判断方程是否表示椭圆】【典例4】（2023·高二课时练习）已知条件：，条件：表示一个椭圆，则是的（    ）A．充分不必要条件 B．必要不充分条件C．充要条件 D．既不充分也不必要条件【答案】B【详解】由，若，则表示一个圆，充分性不成立；而表示一个椭圆，则成立，必要性成立.所以是的必要不充分条件.故选：B【题型5 求标准方程】【典例5】（2023秋·辽宁沈阳·高二东北育才双语学校校考期末）已知椭圆（）的一个焦点为，则（    ）A． B．3 C．41 D．9【答案】A【详解】由题意可知：椭圆的焦点在y轴上，且，则.故选：A.【题型6根据椭圆的标准方程研究其几何性质】【典例6】（2023春·上海杨浦·高二校考期中）椭圆与椭圆的（    ）A．长轴相等 B．短轴相等 C．焦距相等 D．长轴、短轴、焦距均不相等【答案】C【详解】椭圆即，则此椭圆的长轴长为10，短轴长为6，焦距为；椭圆即，因为，则此椭圆的长轴长为，短轴长为，焦距为,故两个椭圆的焦距相等．故选：C．【题型7根据椭圆的几何性质求其标准方程 】焦点的位置焦点在轴上焦点在轴上图形标准方程（）（）范围，，顶点，，，轴长短轴长＝，长轴长＝焦点焦距对称性对称轴：轴、轴　对称中心：原点离心率，【典例7】（2023秋·新疆乌鲁木齐·高二乌鲁木齐市第十九中学校考期末）过点且与椭圆有相同焦点的椭圆方程为（    ）A． B． C． D．【答案】C【详解】由化简可得，焦点为在轴上，同时又过点，设，有，解得，故选：C【题型8求椭圆的离心率的值】离心率：椭圆焦距与长轴长之比：. （） 当越接近1时，越接近，椭圆越扁；当越接近0时，越接近0，椭圆越接近圆；当且仅当时，图形为圆，方程为【典例8】（2023·海南海口·海南华侨中学校考模拟预测）已知，分别是椭圆：（）的左，右焦点，是上的一点，若，且，则的离心率为（    ）A． B． C． D．【答案】C【详解】在中，，设，由题意知,，由余弦定理得,，由椭圆定义知，则离心率.【题型9直线与椭圆的位置关系】【典例9】（2023·全国·高三对口高考）若直线与椭圆有且只有一公共点，那么的值为（    ）A． B． C． D．【答案】C【详解】因为方程表示的曲线为椭圆，则，将直线的方程与椭圆的方程联立，，可得，则，解得.故选：C.【题型10弦长】弦长公式：若直线与圆锥曲线相交与、两点，则：         弦长                             弦长这里的求法通常使用韦达定理，需作以下变形：；   【典例10】（2023·全国·高三对口高考）已知椭圆，过左焦点作倾斜角为的直线交椭圆于、两点，则弦的长为         ．【答案】【详解】在椭圆中，，，则，故点，设点、，由题意可知，直线的方程为，即，联立可得，，由韦达定理可得，，所以，.故答案为：.练习1.（2023·高二课时练习）已知椭圆以原点为中心，长轴长是短轴长的2倍，且过点，求此椭圆的标准方程．【答案】或【详解】当焦点在轴上时，设椭圆方程，则，解得，故椭圆方程为；当焦点在轴上时，设椭圆方程，则，解得，故椭圆方程为；综上，椭圆方程为或.2.（2023·全国·高三专题练习）已知焦点在轴上的椭圆的焦距等于，则实数的值为（    ）A．或 B．或 C． D．【答案】D【详解】因为椭圆的焦点在轴上，所以，根据题意可得，解得.故选：D.3.（2023秋·高二课时练习）设分别为椭圆的左右焦点，过的直线交椭圆于A、B两点，则的周长为（    ）A．12 B．24 C． D．【答案】D【详解】由题意可得，对于椭圆有长半轴长，又过的直线交椭圆于A、B两点，故的周长，故选：D4.（2023春·江苏南京·高二江苏省江浦高级中学校联考阶段练习）已知椭圆的左、右焦点为，且过点则椭圆标准方程为           ．【答案】【详解】由题知：，①又椭圆经过点，所以，②又，③联立解得：，故椭圆的标准方程为：.故答案为：.5.（2023秋·四川成都·高二统考期末）椭圆上一点P与它的一个焦点的距离等于6，那么点P与另一个焦点的距离等于      .【答案】14【详解】设左、右焦点为, 设，由题得因为，所以.所以点P与另一个焦点的距离等于14.故答案为：14故选：B. 6.（2023秋·高二单元测试）已知点是椭圆上一点，椭圆的左、右焦点分别为、，且，则的面积为（    ）A．6 B．12 C． D．【答案】C【详解】由椭圆，得，，.  设，，∴，在中，由余弦定理可得：，可得，得，故.7.（2023·全国·高三对口高考）已知椭圆的焦点为、，点在椭圆上，若，则        ，的大小为        .【答案】     2     【详解】∵，，∴，∴，又，，∴，由余弦定理，得，∴.故答案为：2，8.（2023春·河北石家庄·高二正定中学校考阶段练习）若椭圆的离心率为，则椭圆的长轴长为           .【答案】或【详解】因为椭圆的离心率为，易知，当时，椭圆焦点在轴上，，，所以，解得，则，所以椭圆的长轴长为.当时，椭圆焦点在轴上，，，所以，得，满足题意，此时，所以椭圆的长轴长为.故答案为：或.9.（2023春·江西吉安·高二校考期中）直线与椭圆的位置关系是（       ）A．相离 B．相切 C．相交 D．无法确定【答案】C【详解】联立，则所以方程有两个不相等的实数根，所以直线与椭圆相交故选：C.10.（2023·全国·高三对口高考）通过椭圆的焦点且垂直于x轴的直线l被椭圆截得的弦长等于（    ）A． B．3 C． D．6【答案】B【详解】由题设，不妨设过焦点且垂直于x轴的直线，代入椭圆方程得，可得，故被椭圆截得的弦长等于.故选：B11.（2023秋·浙江湖州·高二统考期末）椭圆的长轴长、短轴长、离心率依次是（    ）A． B． C． D．【答案】D【详解】由已知，可得椭圆标准方程为，则，，，所以长轴长为、短轴长为、离心率为.故选：D.12.（2023·全国·高三专题练习）若椭圆的离心率为，则椭圆的长轴长为（    ）A．6 B．或 C． D．或【答案】D【详解】当焦点在轴时，由，解得，符合题意，此时椭圆的长轴长为；当焦点在轴时，由，解得，符合题意，此时椭圆的长轴长为．故选：D．13.（2023秋·高二课时练习）椭圆的焦距为4，则m的值为          ．【答案】10或2【详解】椭圆的焦距为4，即当时，；当时，；故m的值为10或2，故答案为：10或214.（2023春·四川泸州·高二四川省泸县第四中学校考期末）已知椭圆的对称轴是坐标轴，离心率为，长轴长为12，则椭圆方程为（    ）A． B．C．或 D．【答案】C【详解】由题意知，，，所以，，∴，又因为椭圆的对称轴是坐标轴，则焦点可能在或轴上.∴椭圆方程：或故选：C15.（2023秋·广东江门·高二台山市华侨中学校考期中）已知椭圆焦点在轴，它与椭圆有相同离心率且经过点，则椭圆标准方程为      .【答案】【详解】椭圆的离心率为，设所求椭圆方程为，则，从而，，又，∴，∴所求椭圆的标准方程为.故答案为： .