
第二单元 图形的轴对称(能力提升)(原卷版)
展开
这是一份第二单元 图形的轴对称(能力提升)(原卷版),共8页。
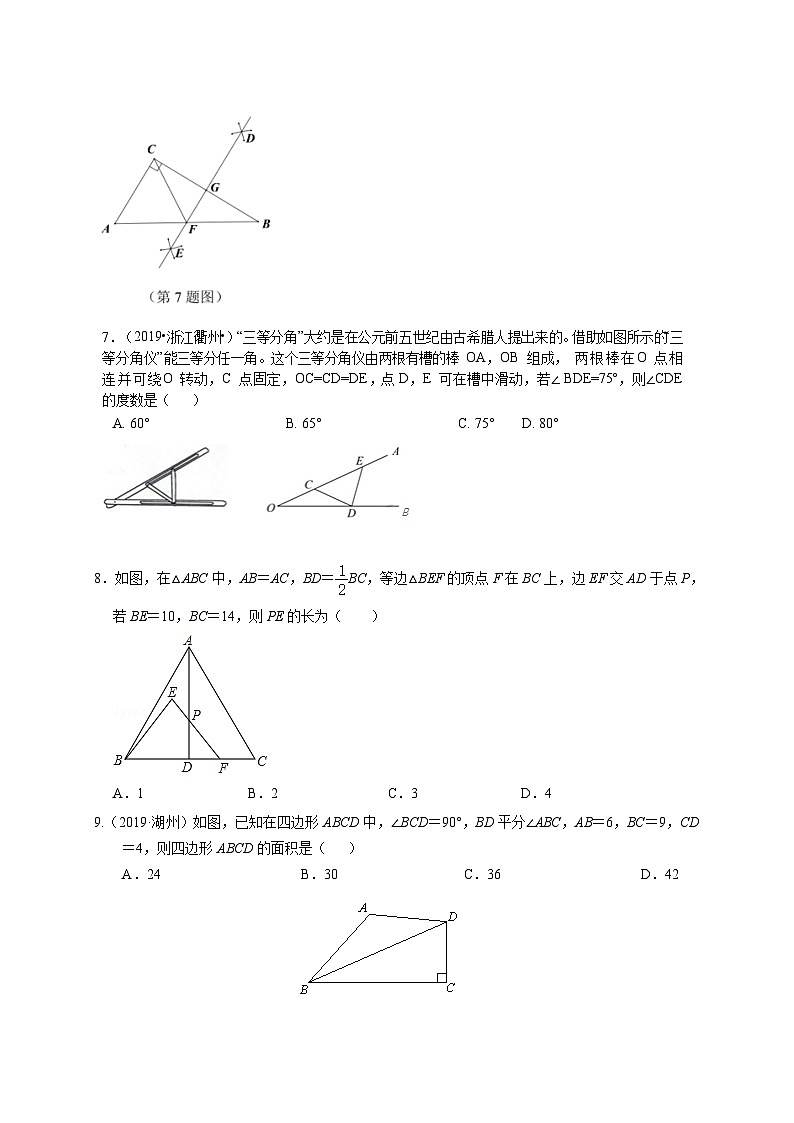
第二单元 图形的轴对称(青岛版) (能力提升)班级___________ 姓名___________ 学号____________ 分数____________(考试时间:120分钟试卷;满分:120分)注意事项:1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分。答卷前,考生务必将自己的班级、姓名、学号填写在试卷上。2.回答第I卷时,选出每小题答案后,将答案填在选择题的答题表中。3.回答第II卷时,将答案直接写在试卷上。第Ⅰ卷(选择题共36分)一、选择题(每小题3分,共36分)1.(2019•北京)下列倡导节约的图案中,是轴对称图形的是A. B. C. D.2.(2020·青海)剪纸是我国传统的民间艺术.将一张纸片按图中①,②的方式沿虚线依次对折后,再沿图③中的虚线裁剪,最后将图④中的纸片打开铺平,所得图案应该是( )A. B. C. D.3.如图,△ABC与△A′B′C′关于直线l对称,且∠A=105°,∠C′=30°,则∠B=( )A.25° B.45° C.30° D.20°4.下列说法正确的是( )A.能够完全重合的两个图形成轴对称 B.全等的两个图形成轴对称 C.形状一样的两个图形成轴对称 D.沿着一条直线对折能够重合的两个图形成轴对称5.如图,经过直线AB外一点C作这条直线的垂线,作法如下:(1)任意取一点K,使点K和点C在AB的两旁.(2)以点C为圆心,CK长为半径作弧,交AB于点D和E.(3)分别以点D和点E为圆心,大于DE的长为半径作弧,两弧相交于点F.(4)作直线CF.则直线CF就是所求作的垂线.根据以上尺规作图过程,若将这些点作为三角形的顶点,其中不一定是等腰三角形的为( )A.△CDF B.△CDK C.△CDE D.△DEF6.(2019•山东省东营市)如图,在Rt△ABC中,∠ACB=90°,分别以点B和点C为圆心,大于BC的长为半径作弧,两弧相交于D、E两点,作直线DE交AB于点F,交BC于点G,连结CF,若AC=3,CG=2,则CF的长为( )A. B.3 C.2 D.7.(2019•浙江衢州•)“三等分角”大约是在公元前五世纪由古希腊人提出来的。借助如图所示的“三等分角仪”能三等分任一角。这个三等分角仪由两根有槽的棒 OA,OB 组成, 两根棒在O 点相连并可绕O 转动,C 点固定,OC=CD=DE,点 D,E 可在槽中滑动,若∠ BDE=75°,则∠CDE 的度数是( )A. 60° B. 65° C. 75° D. 80° 8.如图,在△ABC中,AB=AC,BD=BC,等边△BEF的顶点F在BC上,边EF交AD于点P,若BE=10,BC=14,则PE的长为( )A.1 B.2 C.3 D.49.(2019·湖州)如图,已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是( )A.24 B.30 C.36 D.4210.(2020·衢州市)如图,把一张矩形纸片ABCD按所示方法进行两次折叠,得到等腰直角三角形BEF,若BC=1,则AB的长度为( )A. B. C. D.11.如图,∠AOB=30°,M,N分别是边OA,OB上的定点,P,Q分别是边OB,OA上的动点,记∠OPM=α,∠OQN=β,当MP+PQ+QN最小时,则关于α,β的数量关系正确的是( )A.β﹣α=60° B.β+α=210° C.β﹣2α=30° D.β+2α=240°12.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过O点作EF∥BC交AB于点E,交AC于点F,过点O作OD⊥AC于D,下列四个结论.①EF=BE+CF②∠BOC=90°+∠A③点O到△ABC各边的距离相等 ④设OD=m,AE+AF=n,则S△AEF=mn,正确的结论有( )个.A.1个 B.2个 C.3个 D.4个 第II卷(非选择题 共64分)二、填空题(每小题3分,共18分)13.(2019•兰州)在△ABC中,AB=AC,∠A=40°,则∠B=__________.14. 如图,在△ABC中,AB=AC,D是AB延长线上一点,E是BC延长线上一点,F是CA延长线上一点,∠DBC=130°,则∠FAB的度数为 .15.(2020年山东省潍坊市中考数学试卷)如图,在Rt△ABC中,∠C=90°,∠B=20°,PQ垂直平分AB,垂足为Q,交BC于点P.按以下步骤作图:①以点A为圆心,以适当的长为半径作弧,分别交边AC,AB于点D,E;②分别以点D,E为圆心,以大于DE的长为半径作弧,两弧相交于点F;③作射线AF.若AF与PQ的夹角为α,则α= °.16.(2020年上内蒙古中考数学试卷)如图,在△ABC中,∠ACB=90°,AC=BC,点P在斜边AB上,以PC为直角边作等腰直角三角形PCQ,∠PCQ=90°,则PA2,PB2,PC2三者之间的数量关系是 .17. 如图,已知∠MON,在边ON 上顺次取点P1,P3,P5 …,在边OM 上顺次取点P2,P4,P6 …,使得OP1=P1P2=P2P3=P3P4=P4P5 …,得到等腰△OP1P2,△P1P2P3,△P2P3P4,△P3P4P5 …(1)若∠MON=30°,可以得到的最后一个等腰三角形是 ;(2)若按照上述方式操作,得到的最后一个等腰三角形是△P3P4P5,则∠MON 的度数α 的取值范围是 .18.(2020年上海市中考数学试卷)如图,在△ABC中,AB=4,BC=7,∠B=60°,点D在边BC上,CD=3,联结AD.如果将△ACD沿直线AD翻折后,点C的对应点为点E,那么点E到直线BD的距离为 .三、解答题(共46分)19.(6分)利用6×8正方形网格画图(不写画法,保留画图痕迹):(1)画出△ABD的对称轴直线l;(2)画△ADE,使得△ADE与△BDC关于直线l对称;(3)画格点F,使得△ABF是以AB为斜边的直角三角形.20.(8分)已知,a、b、c为△ABC的三边长,b、c满足(b﹣2)2+|c﹣3|=0,且a为方程|a﹣4|=2的解,求△ABC的周长,并判断△ABC的形状.21.(8分)(2019山东枣庄)如图,BD是菱形ABCD的对角线,∠CBD=75°,(1)请用尺规作图法,作AB的垂直平分线EF,垂足为E,交AD于F;(不要求写作法,保留作图痕迹)(2)在(1)条件下,连接BF,求∠DBF的度数.22.(8分)(1)如图1,已知△ABC,请画出△ABC关于直线AC对称的三角形.(2)如图2,若△ABC与△DEF关于直线l对称,请作出直线l(请保留作图痕迹)(3)如图3,在矩形ABCD中,已知点E,F分别在AD和AB上,请在边BC上作出点G,在边CD作出点H,使得四边形EFGH的周长最小.23.(8分)如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.(1)若BC=10,则△ADE周长是多少?为什么?(2)若∠BAC=128°,则∠DAE的度数是多少?为什么?24.(8分)如图,在△ABC中,AB=AC,∠BAC=90°,点D是边BC上的动点,连接AD,点C关于直线AD的对称点为点E,射线BE与射线AD交于点F.(1)在图中,依题意补全图形;(2)记∠DAC=α (α<45° ),求∠ABF 的大小;(用含α 的式子表示)(3)若△ACE是等边三角形,猜想EF和BC的数量关系,并证明.25.(8分)如图(a),已知点B(0,6),点C为x轴上一动点,连接BC,△ODC和△EBC都是等边三角形.(1)求证:BO=DE.(2)如图(b),当点D恰好落在BC上时,①求OC的长及点E的坐标;②在x轴上是否存在点P,使得△PEC为等腰三角形?若存在,写出点P的坐标;如不存在,说明理由.③如图(c),点M是线段BC上的动点(点B,C除外),过点M作MG⊥BE于点G,MH⊥CE于点H,当点M运动时,MH+MG的值是否发生变化?如不会变化,直接写出MH+MG的值;如会变化,简要说明理由.






