
第一单元 图形的相似(基础过关)(原卷版
展开
这是一份第一单元 图形的相似(基础过关)(原卷版,共8页。
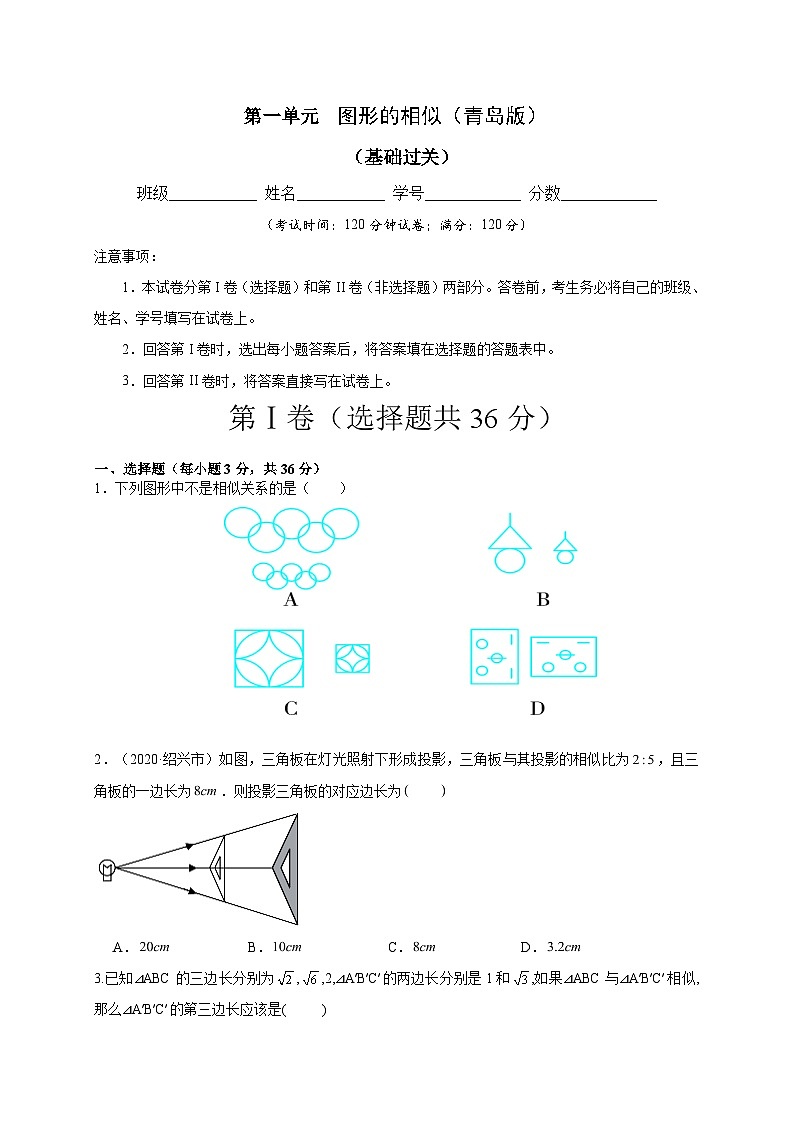
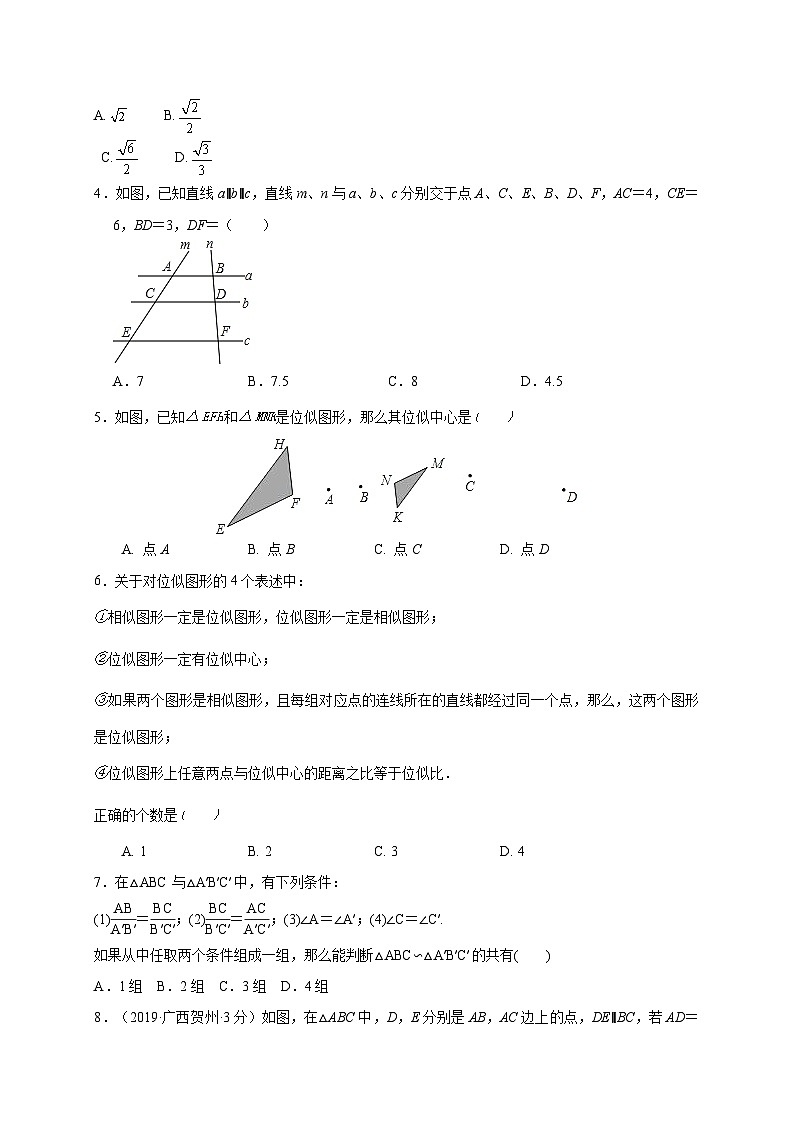
第一单元 图形的相似(青岛版) (基础过关)班级___________ 姓名___________ 学号____________ 分数____________(考试时间:120分钟试卷;满分:120分)注意事项:1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分。答卷前,考生务必将自己的班级、姓名、学号填写在试卷上。2.回答第I卷时,选出每小题答案后,将答案填在选择题的答题表中。3.回答第II卷时,将答案直接写在试卷上。第Ⅰ卷(选择题共36分) 一、选择题(每小题3分,共36分)1.下列图形中不是相似关系的是( ) 2.(2020·绍兴市)如图,三角板在灯光照射下形成投影,三角板与其投影的相似比为,且三角板的一边长为.则投影三角板的对应边长为 A. B. C. D.3.已知⊿ABC的三边长分别为,,2,⊿A′B′C′的两边长分别是1和,如果⊿ABC与⊿A′B′C′相似,那么⊿A′B′C′的第三边长应该是( )A. B. C. D.4.如图,已知直线a∥b∥c,直线m、n与a、b、c分别交于点A、C、E、B、D、F,AC=4,CE=6,BD=3,DF=( )A.7 B.7.5 C.8 D.4.55.如图,已知和是位似图形,那么其位似中心是
A. 点A B. 点B C. 点C D. 点D6.关于对位似图形的4个表述中:相似图形一定是位似图形,位似图形一定是相似图形;位似图形一定有位似中心;如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么,这两个图形是位似图形;位似图形上任意两点与位似中心的距离之比等于位似比.正确的个数是 A. 1 B. 2 C. 3 D. 47.在△ABC与△A′B′C′中,有下列条件:(1)=;(2)=;(3)∠A=∠A′;(4)∠C=∠C′.如果从中任取两个条件组成一组,那么能判断△ABC∽△A′B′C′的共有( )A.1组 B.2组 C.3组 D.4组8.(2019·广西贺州·3分)如图,在△ABC中,D,E分别是AB,AC边上的点,DE∥BC,若AD=2,AB=3,DE=4,则BC等于( )@z~step.co*m]A.5 B.6 C.7 D.89.(2019年山东省淄博枣庄市中考数学试卷)如图,在△ABC中,AC=2,BC=4,D为BC边上的一点,且∠CAD=∠B.若△ADC的面积为a,则△ABD的面积为( )A.2a B.a C.3a D.a10.如图,AD是△ABC的中线,E是AD上一点,AE:ED=1:3,BE的延长线交AC于F,AF:FC=( )A.1:3 B.1:4 C.1:5 D.1:611.如图,点E,点F分别在菱形ABCD的边AB,AD上,且AE=DF,BF交DE于点G,延长BF交CD的延长线于H,若=2,则的值为( )A. B. C. D.12.如图,在△ABC中,D、E分别是AB、AC的中点,连接BE,CD相交于点O,连接DE,下列结论:①=;②=;③=;④=,其中正确的个数有( )A1个 B2个 C3个 D4个 第II卷(非选择题 共64分)二、填空题(每小题3分,共18分)13.(2019•长沙)如图,要测量池塘两岸相对的A,B两点间的距离,可以在池塘外选一点C,连接AC,BC,分别取AC,BC的中点D,E,测得DE=50 m,则AB的长是__________m.14.如图,在平面直角坐标系中,已知A(1,0),D(3,0),△ABC与△DEF位似,原点O是位似中心.若AB=1.5,则DE= .15..如图,在正方形ABCD中,E是BC边上一点,且BE∶EC=2∶1,AE与BD交于点F,则△AFD与四边形DFEC的面积之比是 .16.(2020·湖州市)在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点,顶点都是格点的三角形称为格点三角形.如图,已知是网格图形中的格点三角形,则该图中所有与相似的格点三角形中.面积最大的三角形的斜边长是 .17.(2019•南京)如图,在△ABC中,BC的垂直平分线MN交AB于点D,CD平分∠ACB.若AD=2,BD=3,则AC的长为__________.18.如图,在△ABC中,分别以AC,BC为边作等边△ACD和等边△BCE.设△ACD、△BCE、△ABC的面积分别是S1、S2、S3,现有如下结论:①S1:S2=AC2:BC2;②连接AE,BD,则△BCD≌△ECA;③若AC⊥BC,则S1•S2=S32.其中结论正确的序号是 .三、解答题(共46分)19.(6分)如图所示,图中的小方格都是边长为1的正方形,与是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.画出位似中心点O;直接写出与的位似比;以位似中心O为坐标原点,以格线所在直线为坐标轴建立平面直角坐标系,并直接写出各顶点的坐标. 20.(8分)(2020年山东省济宁市中考数学试卷)如图,在△ABC中,AB=AC,点P在BC上.(1)求作:△PCD,使点D在AC上,且△PCD∽△ABP;(要求:尺规作图,保留作图痕迹,不写作法)(2)在(1)的条件下,若∠APC=2∠ABC.求证:PD∥AB.21.(8分)如图,一条小河的两岸有一段是平行的,在河的一岸每隔6 m有一棵树,在河的对岸每隔60 m有一根电线杆,在有树的一岸离岸边30 m处可看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两棵树之间还有三棵树,求河的宽度. 22.(8分)如图,在Rt△ABC中,AD是斜边BC上的高,∠ABC的平分线BE交AC于E,交AD于F.求证:=.23.(8分)如图,Rt△ABC中,∠ACB=90°,AB的中垂线交边BC于点E,交AC的延长线于点F,连结AE.(1)求证:△ADE∽△FDA;(2)若DE=EF=1,求AE的长.24.(8分)(2019•四川省凉山州)如图,∠ABD=∠BCD=90°,DB平分∠ADC,过点B作BM∥CD交AD于M.连接CM交DB于N.(1)求证:BD2=AD•CD;(2)若CD=6,AD=8,求MN的长.25.(8分)(2020年山东省泰安市中考数学试卷)小明将两个直角三角形纸片如图(1)那样拼放在同一平面上,抽象出如图(2)的平面图形,∠ACB与∠ECD恰好为对顶角,∠ABC=∠CDE=90°,连接BD,AB=BD,点F是线段CE上一点.探究发现:(1)当点F为线段CE的中点时,连接DF(如图(2)),小明经过探究,得到结论:BD⊥DF.你认为此结论是否成立? .(填“是”或“否”)拓展延伸:(2)将(1)中的条件与结论互换,即:BD⊥DF,则点F为线段CE的中点.请判断此结论是否成立.若成立,请写出证明过程;若不成立,请说明理由.问题解决:(3)若AB=6,CE=9,求AD的长.






