

七年级初中数学拔高卷第一二单元
展开2023年7月10日初中数学作业
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.一跳蚤在一直线上从点开始,第次向右跳个单位,紧接着第2次向左跳个单位,第次向右跳个单位,第次向左跳个单位,……,依此规律跳下去,当它跳第次落下时,落点处离点的距离是( )个单位.
A. B. C. D.
2.在数轴上和有理数a、b、c对应的点的位置如图所示,有下列四个结论:
①;②;③;④,其中正确的结论有( )个
A.4个 B.3个 C.2个 D.1个
3.现有以下五个结论:
①整数和分数统称为有理数;
②绝对值等于其本身的有理数是0和1;
③每一个有理数都可以用数轴上的一个点表示;
④若两个非0数互为相反数,则它们相除的商等于﹣1;
⑤几个有理数相乘,负因数个数是奇数时,积是负数.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
4.如图所示,在这个数据运算程序中,若开始输入的x的值为2,结果输出的是1,返回进行第二次运算则输出的是﹣4,…,则第2020次输出的结果是( )
A.﹣1 B.3 C.6 D.8
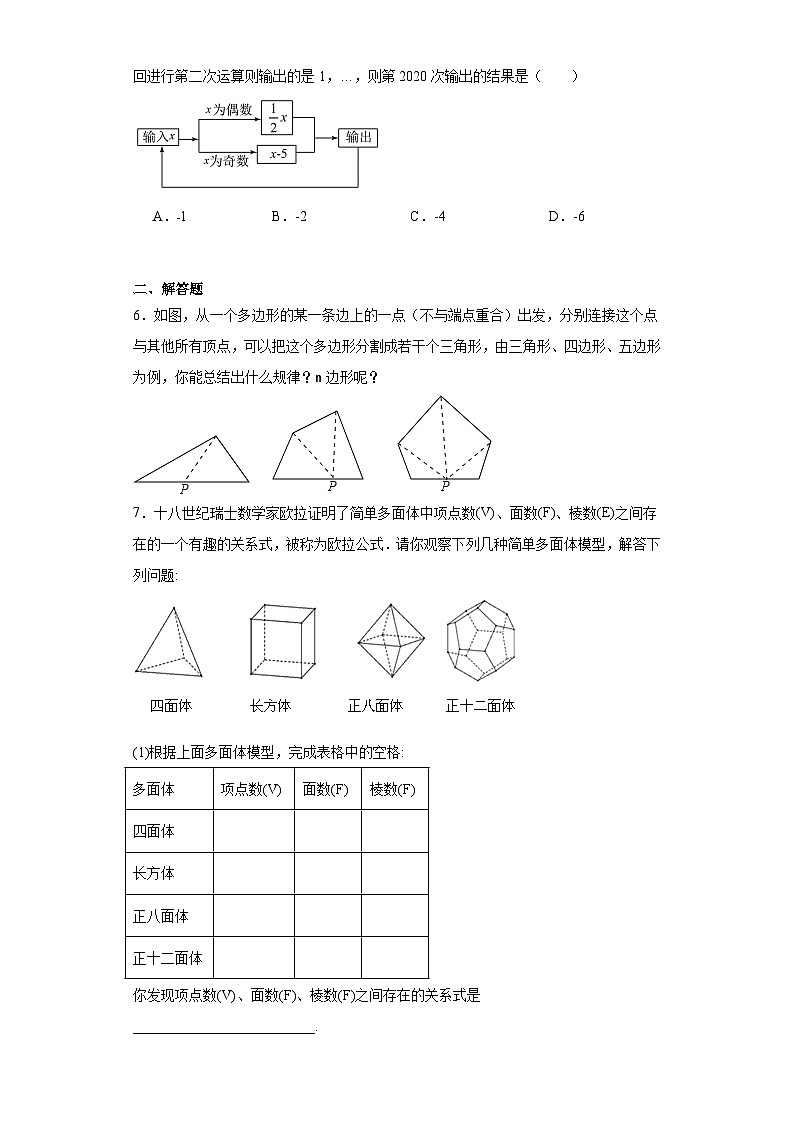
5.如图所示,在这个数据运算程序中,若开始输入的x的值为4,输出的结果是2,返回进行第二次运算则输出的是1,…,则第2020次输出的结果是( )
A.﹣1 B.-2 C.-4 D.-6
二、解答题
6.如图,从一个多边形的某一条边上的一点(不与端点重合)出发,分别连接这个点与其他所有顶点,可以把这个多边形分割成若干个三角形,由三角形、四边形、五边形为例,你能总结出什么规律?n边形呢?
7.十八世纪瑞士数学家欧拉证明了简单多面体中项点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型,解答下列问题:
(1)根据上面多面体模型,完成表格中的空格:
多面体 | 项点数(V) | 面数(F) | 棱数(F) |
四面体 |
|
|
|
长方体 |
|
|
|
正八面体 |
|
|
|
正十二面体 |
|
|
|
你发现项点数(V)、面数(F)、棱数(F)之间存在的关系式是__________________________.
(2)一个多面体的面数比顶点数小8,且有30条棱,则这多面体的顶点数是 20;
(3)某个玻璃饰品的外形是简单多面体,它的外表是由三角形和八边形两种多边形拼接而成,且有48个顶点,每个顶点处都有3条棱,设该多面体表面三角形的个数为x个,八边形的个数为y个,求x+y的值.
8.如图,在数轴上有A、B、C这三个点.
回答:
(1)A、B、C这三个点表示的数各是多少?
(2)A、B两点间的距离是多少?A、C两点间的距离是多少?
(3)若将点A向右移动5个单位后,则A、B、C这三个点所表示的数谁最大?
(4)应怎样移动点B的位置,使点B到点A和点C的距离相等?
9.已知有理数、、在数轴上的位置如图所示,且
(1)求和 的值
(2)化简:
10.观查下列每对数在数轴上的对应点间的距离,3与5,4与﹣2, ﹣4与3, ﹣1与﹣5.并回答下列各题:
(1)数轴上表示4和﹣2两点间的距离是 ;表示﹣1和﹣5两点间的距离是 .
(2)若数轴上的点A表示的数为x,点B表示的数为﹣3.
①数轴上A、B两点间的距离可以表示为 (用含x的代数式表示);
②如果数轴上A、B两点间的距离为|AB|=1,求x的值.
(3)直接写出代数式的最小值为 .
11.观察下列等式=1﹣,=﹣,=﹣,将以上三个等式两边分别相加得++=1﹣+﹣+﹣=1﹣=.
(1)猜想并写出 ;
(2)+++…+= ;
(3)探究并计算:;
(4)计算:.
三、填空题
12.在数轴上表示有理数a,b,c的三点如图所示,若ac<0,b+a<0,则①;②b+c<0,③abc<0,其中正确的是 (只填序号).
参考答案:
1.B
【分析】设向右为正,向左为负.根据正负数的意义列出式子计算即可.
【详解】解:设向右为正,向左为负.则
1+(-2)+3+(-4)+.+(-100)=[1+(-2)]+[3+(-4)]+.+[99+(-100)]=-50.
∴落点处离O点的距离是50个单位.
故答案为:B.
【点睛】此题主要考查正负数在实际生活中的应用,所以学生在学这一部分时一定要联系实际,不能死学.
2.B
【分析】根据三点与1的位置关系即可判断①;对于②,根据a、b、c的位置关系化简方程左端,判断是否等于右端即可;对于③,首先判断三个式子的正负,然后判断积的符号;对于④,首先判断1−bc的符号,然后和a比较即可 .
【详解】①∵a<1,b<1,c<1
∴a-1<0,b-1<0,c-1<0
∴,故①正确;
②∵a<b,b<c,a<c
∴a-b<0,b-c<0,a-c<0
∴,
∴,故②正确;
③∵a+b<0,b+c>0,a+c<0
∴,故③正确;
④∵a<-1
∴|a|>1
∵0<b<c<1
∴0<bc<1
∴1-bc<1
∴|a|>1-bc,故④错误;
故选B
【点睛】本题考查了数轴,有理数,绝对值的化简,题目较难,英重点关注数轴上点和已知数的位置关系,然后进行推导求解.
3.C
【分析】②中绝对值等于其本身的有理数是0和正数,故原结论错误;
⑤种几个有理数相乘,负因数个数为奇数,则乘积为负数,也有可能是0,此结论错误.
【详解】①整数和分数统称为有理数,此结论正确;
②绝对值等于其本身的有理数是0和正数,故原结论错误;
③每一个有理数都可以用数轴上的一个点表示,此结论正确;
④若两个非0数互为相反数,则它们相除的商等于﹣1,此结论正确;
⑤几个有理数相乘,负因数个数为奇数,则乘积为负数,也有可能是0,此结论错误.
∴正确的有①③④共3个.
故选C.
【点睛】本题考查有理数的性质.
4.A
【分析】先根据数据运算程序计算出第1-8次的输出结果,再归纳类推出一般规律,由此即可得.
【详解】第1次运算输出的结果为,
第2次运算输出的结果为,
第3次运算输出的结果为,
第4次运算输出的结果为,
第5次运算输出的结果为,
第6次运算输出的结果为,
第7次运算输出的结果为,
第8次运算输出的结果为,
归纳类推得:从第2次运算开始,输出结果是以循环往复的,
因为,
所以第2020次运算输出的结果与第4次输出的结果相同,即为,
故选:A.
【点睛】本题考查了程序图与有理数计算的规律性问题,正确归纳类推出一般规律是解题关键.
5.B
【分析】先根据数据运算程序计算出第1-9次的输出结果,再归纳类推出一般规律,由此即可得.
【详解】第1次运算输出的结果为,
第2次运算输出的结果为,
第3次运算输出的结果为,
第4次运算输出的结果为,
第5次运算输出的结果为,
第6次运算输出的结果为,
第7次运算输出的结果为,
第8次运算输出的结果为,
第9次运算输出的结果为,
归纳类推得:从第3次运算开始,输出结果是以循环往复的,
因为,
所以第2020次运算输出的结果与第4次输出的结果相同,即为,
故选:B.
【点睛】本题考查了数字类的规律性问题,正确归纳类推出一般规律是解题关键.
6.n边形被分为(n﹣1)个三角形.
【详解】试题分析:
分别列举出以三角形,四边形,五边形为例时图形中三角形的个数,再由此总结出规律.
试题解析:
由图中可以看出三角形被分为2个三角形;四边形被分为3个三角形,五边形被分为4个三角形,那么n边形被分为(n﹣1)个三角形.
点睛:这是一个与图形相关的规律问题,基本的方法是,分别列举出几个图形中的三角形的个数,从三角形的个数的变化与图形的边数的变化中找出规律,从有限到无限,写出相应的代数式.
7.(1) 见解析,V+F-E=2;(2) 20;(3)26
【分析】(1)观察表格可以看出:顶点数+面数-棱数=2,关系式为:V+F-E=2;
(2)代入(1)中公式进行计算;
(3)根据欧拉公式可得顶点数+面数-棱数=2,然后表示出棱数,进而可得面数.
【详解】解:(1)根据题意得如下图
多面体 | 顶点数(V) | 面数(F) | 棱数(E) |
四面体 | 4 | 4 | 6 |
长方体 | 8 | 6 | 12 |
正八面体 | 6 | 8 | 12 |
正十二面体 | 20 | 12 | 30 |
∵4+4-6=2,8+6-12=2,6+8-12=2,
∴顶点数(V)、面数(F)、棱数(E)之间存在的关系式是V+F-E=2;
(2)由(1)可知:V+F-E=2,
∵一个多面体的面数比顶点数小8,且有30条棱,
∴V+V-8-30=2,即V=20;
(3)∵有48个顶点,每个顶点处都有3条棱,两点确定一条直线;
∴共有48×3÷2=72条棱,
设总面数为F,
48+F-72=2,
解得F=26,
∴x+y=26.
【点睛】本题考查了多面体的顶点数,面数,棱数之间的关系及灵活运用,得出欧拉公式是解题关键.
8.(1)A:-6,B:1,C:4;(2)AB距离为7,AC距离为10;(3)C;(4)向左移动2个单位
【分析】(1)直接读图即可得到;
(2)用右侧数字减左侧数字即为两点间的距离;
(3)先得出A移动后的数字,再比较着3个数字的大小;
(4)AC间的距离为10,故只需AB、BC间的距离都是5即可
【详解】(1)观察数轴得:A:-6,B:1,C:4;
(2)AB的距离为:1-(-6)=7;
AC的距离为:4-(-6)=10;
(3)A向右移动5个单位变为:-1
则A、B、C此刻分别为:-1、1、4,其中4最大,即点C;
(4)∵AC的距离为10
∴要使得AB、BC距离相等,则AB、BC都为5
∴只需将点B向左移动2个单位即可
【点睛】本题是数轴的考查,解题关键是先读懂数轴,得出对应数值,然后根据向左移动为减,向右移动为加,按照题干变换求解
9.(1);;(2).
【分析】(1)根据且a、b位于原点两侧,得到a、b互为相反数,然后进行求解即可;
(2)先分别判定绝对值内的数的大小,再去绝对值,再合并同类项即可求解.
【详解】(1)∵且a、b位于原点两侧
∴a、b互为相反数
∴,
(2)如图可得:c<b<0<a且
∴a>0,a=-b即a+b=0,c-a<0,c-b<0,-2b>0
因此
=
=
=
【点睛】本题考查了根据数轴取绝对值进行计算的问题,其中根据去掉绝对值是解答本题的关键.
10.(1)6 4 (2)①丨x+3丨 ②-2或者-4 (3)5
【分析】距离一定是个非负数.
【详解】(1)数轴上表示4和﹣2两点间的距离是6;表示﹣1和﹣5两点间的距离是4.
(2)距离是个非负数,故值一定要加绝对值.
令丨x-(-3)丨=1,解得:x=-2或者-4
(3)当时,代数式的最小值为
当时,代数式的最小值为5
当时,代数式的最小值
综合以上,可知代数式的最小值为5.
【点睛】本题考查数轴的相关知识和绝对值的运用.
11.(1);(2);(3);(4).
【分析】(1)观察已知等式,进行归纳类推即可得;
(2)根据(1)中的猜想进行计算即可得;
(3)先根据乘法分配律提取,再参照(2)进行计算即可得;
(4)先根据乘法分配律提取,再参照(2)进行计算即可得.
【详解】(1),
,
,
归纳类推得:,
故答案为:;
(2),
,
,
,
故答案为:;
(3),
,
,
,
,
;
(4),
,
,
,
,
,
.
【点睛】本题考查了有理数乘法与加减法的规律性问题,依据题意,正确归纳类推出一般规律是解题关键.
12.①
【分析】由数轴知,,但a、b、c是正数还是负数未知,需要分情况讨论;根据ac<0,b+a<0,可知a、c异号,且,但b是正是否不可知.
【详解】由,ac<0,b+a<0可知,,,故①正确;
由于b是正是否不可知,故b+c可能为正,也可能为负,故②错误;
b+c可能为正,也可能为负,ac<0,故abc可能为正,也可能为负,故③错误.
【点睛】本题考查数轴的综合应用.









