山东省德州市禹城市综合高中2023-2024学年高三数学上学期10月月考试题（Word版附解析）

这是一份山东省德州市禹城市综合高中2023-2024学年高三数学上学期10月月考试题（Word版附解析），共19页。试卷主要包含了选择题，多项选择题等内容，欢迎下载使用。
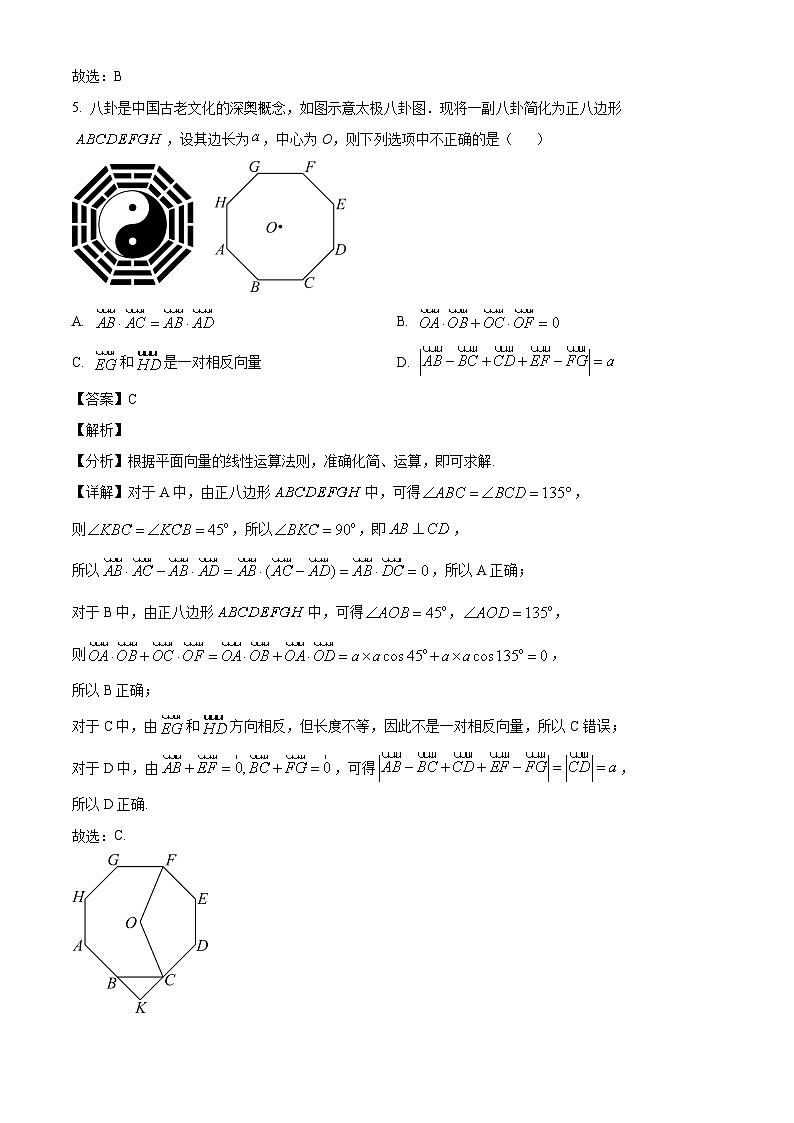
高三10月份月考数学试题（满分150分  时间120分钟）一、选择题：本大题共8小题，每小题5分，共40分.只有一项是符合题目要求的.1. 设集合，，则（    ）A.  B.  C.  D. 【答案】C【解析】【分析】根据一元二次不等式的解法求出集合，根据集合的特征求出集合，然后利用集合的运算即可求解.【详解】集合或，集合，所以，则，故选：.2. 如图，在平行四边形中，为对角线的交点，为的中点，为的中点，若，则（    ）  A. 1 B. 2 C.  D. 【答案】B【解析】【分析】利用平面向量的线性运算法则，求得,进而求得的值，进一步计算即可.【详解】如图：  因为,所以故选：3. 设等比数列的公比为q，则是为单调递增数列的（    ）A. 充分不必要条件 B. 必要不充分条件C. 充要条件 D. 既不充分也不必要条件【答案】D【解析】【分析】通过做差，结合充分条件、必要条件的定义判断即可【详解】若,则,则为单调递减数列所以是为单调递增数列的不充分条件若为单调递增数列,则,则即或,所以故是为单调递增数列的不必要条件故是为单调递增数列既不充分也不必要条件故选：D4. 已知向量，，向量在向量上的投影向量的坐标为（    ）A.  B.  C.  D. 【答案】B【解析】【分析】根据投影向量的定义计算即可.详解】由题意易知，，而在上的投影向量为：.故选：B5. 八卦是中国古老文化的深奥概念，如图示意太极八卦图．现将一副八卦简化为正八边形，设其边长为，中心为O，则下列选项中不正确的是（    ）  A.  B. C. 和是一对相反向量 D. 【答案】C【解析】【分析】根据平面向量的线性运算法则，准确化简、运算，即可求解.【详解】对于A中，由正八边形中，可得，则，所以，即，所以，所以A正确；对于B中，由正八边形中，可得，，则，所以B正确；对于C中，由和方向相反，但长度不等，因此不是一对相反向量，所以C错误；对于D中，由，可得，所以D正确.故选：C.  6. 阻尼器是一种以提供运动的阻力，从而达到减振效果的专业工程装置．深圳一高楼平安金融中心的阻尼器减震装置，是亚洲最大的阻尼器，被称为“镇楼神器”，由物理学知识可知，某阻尼器模型的运动过程可近似为单摆运动，其离开平衡位置的位移s（单位；cm）和时间t（单位：s）的函数关系式为，若振幅是2，图像上相邻最高点和最低点的距离是5，且过点，则和的值分别为（    ）A.  B.  C.  D. 【答案】A【解析】【分析】先由振幅得到，再由最高点和最低点的距离为结合勾股定理可得，从而求得，再将代入即可求得，问题得解.【详解】根据题意，由振幅是2易知，故，则是的最高点，不妨记相邻的最低点为，连接，过作轴，过作，交点为，如图，则，，，故，得，又因为，故，得，所以，因为是的点，故，得，即，因为，所以，故，.故选：A. .7. 已知定义在上的函数满足，且是偶函数，当时，，则（    ）A.  B.  C.  D. 3【答案】C【解析】【分析】根据是偶函数和得到是的一个周期，然后利用周期性求函数值即可.【详解】因为是偶函数，所以，则，因为，所以，则是的一个周期，因为，所以，，.故选：C.8. 已知，是方程的两根，且，，则的值为（    ）A.  B.  C. 或 D. 或【答案】B【解析】【分析】由韦达定理得，即，得，再根据两角和的正切公式解决即可.【详解】由题知，，是方程的两根，所以，即，因为，，所以，，所以， 因为，所以，故选：B二、多项选择题：9. 已知函数则（    ）A. 的最小正周期为B. 在上单调递增C. 直线是图象的一条对称轴D. 的图象可由的图象向左平移个单位长度得到【答案】BC【解析】【分析】化简函数解析式，根据正弦型函数的性质判断ABC，结合函数图象变换判断D.【详解】可化为，函数的最小正周期为，A错误；当时，，因为在上单调递增，所以函数在上单调递增，B正确；当时，，所以直线是图象的一条对称轴，C正确；函数的图象向左平移个单位长度得到函数的图象，D错误.故选：BC.10. 已知定义在上的奇函数，，且当时，，则（    ）A. B. 有2个零点C. 在上为减函数D. 不等式的解集是【答案】AD【解析】【分析】根据赋值法可判断A，根据奇函数的性质可判断CB,结合的性质得的图象，数形结合即可判断D.【详解】在中，令，得，故A正确；又为上的奇函数，，，∴至少有三个零点，故B错误；设x1，，且，则，，，∴在上是增函数，由于为奇函数，∴在上也是增函数，故C错误：由题意，画出的图象如图，等价于 或，由图可知不等式的解集为,故D正确.故选:AD11. 已知中，内角A，B，C所对的边分别为a，b，c，且，，若点P是边BC上一点，Q是AC的中点，点O是所在平面内一点，，则下列说法正确的是（    ）A. 若，则B. 若在方向上的投影向量为，则的最小值为C. 若点P为BC中点，则D. 若，则为定值18【答案】ACD【解析】【分析】对于，根据向量加法的运算法则及三角函数的诱导公式化简计算；对于B，易知当时，取得最小值，计算可得；对于C，根据向量加法结合律律及平行四边形法则计算可得；对于D，根据向量数量积运算律计算即可.【详解】解：如图，设BC的中点为E，连接QE，∵，由余弦定理可得：，∴，∴，又，∴，∴，∴，对A选项，∵，∴，∴，又E为中点，∴，又，∴，∴，故A选项正确；对B选项，∵在方向上的投影向量为，∴，又Q是AC的中点，P在BC上，∴当时，PQ最小，此时，故B选项错误；对C选项，若点P为BC的中点，即P与E点重合，∵，∴，∴，故C选项正确；对D选项，∵，∴的平分线与BC垂直，∴是以BC为底边的等腰三角形，∴，又由A选项分析知，∴根据向量数量积的几何意义知，∴，故D选项正确．故选：ACD．  12. 已知函数，则（    ）A. 当时，函数最小值为B. 当时，函数的极大值点为C. 存在实数使得函数在定义域上单调递增D. 若恒成立，则实数的取值范围为【答案】AD【解析】【分析】由函数极值的求解以及极值点的辨析即可判断AB，由在上恒成立即可判断C，分离参数，构造函数求得其最小值，即可判断D.【详解】因为函数，则，其中，当时，则，令，可得，当时，，则函数单调递减，当时，，则函数单调递增，当时，有极小值，即最小值，故A正确；当时，则，令，可得，当时，，则函数单调递减，当时，，则函数单调递增，当时，函数有极小值，则为极小值点，故B错误；假设存在实数使得函数在定义域上单调递增，则在上恒成立，即在上恒成立，所以在上恒成立，因为的值域为，所以函数无最小值，故不存在实数使得函数在定义域上单调递增，故C错误；若恒成立，即在上恒成立，即在上恒成立，令，则，令，则，当时，，则函数单调递减，当时，，则函数单调递增，当时，有极小值，即最小值，所以，故D正确；故选：AD三.填空题（共4小题）13. 已知向量，则与夹角的大小为_____________．【答案】【解析】【分析】根据题意可得，结合平面向量数量积的定义计算即可求解.【详解】由，得，由，得，即，得，所以，又，所以，即与的夹角为.故答案为：.14. 已知，若，，则=     ．【答案】【解析】【详解】因为，所以，又，，整理得解得或（舍去）因此，因为，所以，，15. 已知函数，则______．【答案】【解析】【分析】先求导函数，解出的值，代入函数即可求得.【详解】由已知，，则所以，，所以，.故答案为：.16. 已知，，则______.【答案】0.75【解析】【分析】利用同角三角函数的平方关系及商数关系计算即可.【详解】由同角三角函数的平方关系及已知条件可知：，当，此时，不合题意；当，符合题意；所以.故答案为：四.解答题（共6小题）17. 如图，平行四边形的对角线AC和BD交于点M，E在BC上，且，直线DE与AB的延长线交于点F，记，．  （1）试用，表示、；（2）试用，表示．【答案】（1），；    （2）.【解析】【分析】（1）利用向量加法的平行四边形法则求出，再利用向量减法法则求出作答.（2）利用平行线的性质探求出，再利用向量减法法则求解作答.【小问1详解】平行四边形的对角线AC和BD交于点M，，.【小问2详解】点E在BC上，且，，则，于是，即，，所以18. 已知在中，角A，B，C所对的边分别为a，b，c，且．（1）求角A的大小；（2）若AD平分并交BC于D，且，，求的面积．【答案】（1）；    （2）.【解析】【分析】（1）变形给定的等式，再利用余弦定理求解作答.（2）根据给定条件，结合（1），利用三角形面积定理求出，进而求出计算作答.【小问1详解】因，则，整理得：，在中，由余弦定理得：，而，所以.【小问2详解】在中，AD平分并交BC于D，则，而，显然有，即，则，整理得：，又，由（1）知，，即有，而，解得，所以的面积.19. 设数列的前n项和为，已知，，成等差数列，且.（1）求的通项公式；（2）若，的前n项和为，若对任意正整数n，不等式恒成立，求的最小值.【答案】（1）    （2）【解析】【分析】（1）根据，，成等差数列，可得，再根据与的关系求通项即可；（2）利用裂项相消法求出，从而可求得的范围，即可求出的范围，即可得解.【小问1详解】解：因为，，成等差数列，所以，即，当时，，即，由，得，所以数列是以为公比的等比数列，则，即，所以，所以；【小问2详解】解：，则，因为恒成立，所以，所以的最小值.20. 已知数列的前项和为（1）求数列的通项公式；（2）令，求数列的前项和．【答案】（1）    （2）【解析】【分析】（1）根据等差数列的定义可得数列是等差数列，从而求得，然后利用求得；（2）利用错位相减法求解即可.【小问1详解】因为，，所以数列是首项为，公差为的等差数列，则，所以，当时，，当时，上式也成立，所以；【小问2详解】，，，两式相减得，所以.21. 已知函数存在两个极值点.（1）求的取值范围；（2）求的最小值.【答案】（1）    （2）【解析】【分析】（1）根据极值点的定义可知，即有两个不等正根，由一元二次方程根的分布可构造不等式组求得的取值范围；（2）由（1）可知，由此化简为，令，利用导数可求得，即为所求的最小值.【小问1详解】由题意知：定义域为，；令，则有两个不等正根，，解得：，实数的取值范围为.【小问2详解】由（1）知：，是的两根，则；；令，则，当时，；当时，；在上单调递减，在上单调递增；，即的最小值为.22. 设函数．（1）讨论的单调性;（2）若，求证：．【答案】（1）单调性见解析    （2）证明见解析【解析】【分析】（1）求导可得，再和两种大情况讨论，在时根据导函数的两根的大小关系讨论分析即可；（2）整理所证不等式为，再根据（1）结论得出，再构造证明即可【小问1详解】由题，①当时，，令则，故当时，，单调递增；当时，，单调递减；②当时，令则，：当，即时，在当和时，，单调递增；当时，，单调递减； 当，即时，，单调递增；当，即时，在当和时，，单调递增；当时，，单调递减；综上所述，当时，在上单调递增，在上单调递减；当时，在和上单调递增，在上单调递减；当时，单调递增；当时，在和上单调递增，在上单调递减【小问2详解】由题，即证，即，得. 由（1）可得当时在上单调递减，在上单调递增，故，当且仅当时取等号.设，则，故在上，单调递减；在上，单调递增.故，即，故，故即得证【点睛】本题主要考查了求导分类讨论分析函数单调性的问题，同时也考查了构造函数证明不等式的问题，需要联系前问的结论化简不等式再证明，属于难题