人教版六年级数学上册【课本】六年级（上）第25讲 几何超越提高

这是一份人教版六年级数学上册【课本】六年级（上）第25讲 几何超越提高，共6页。
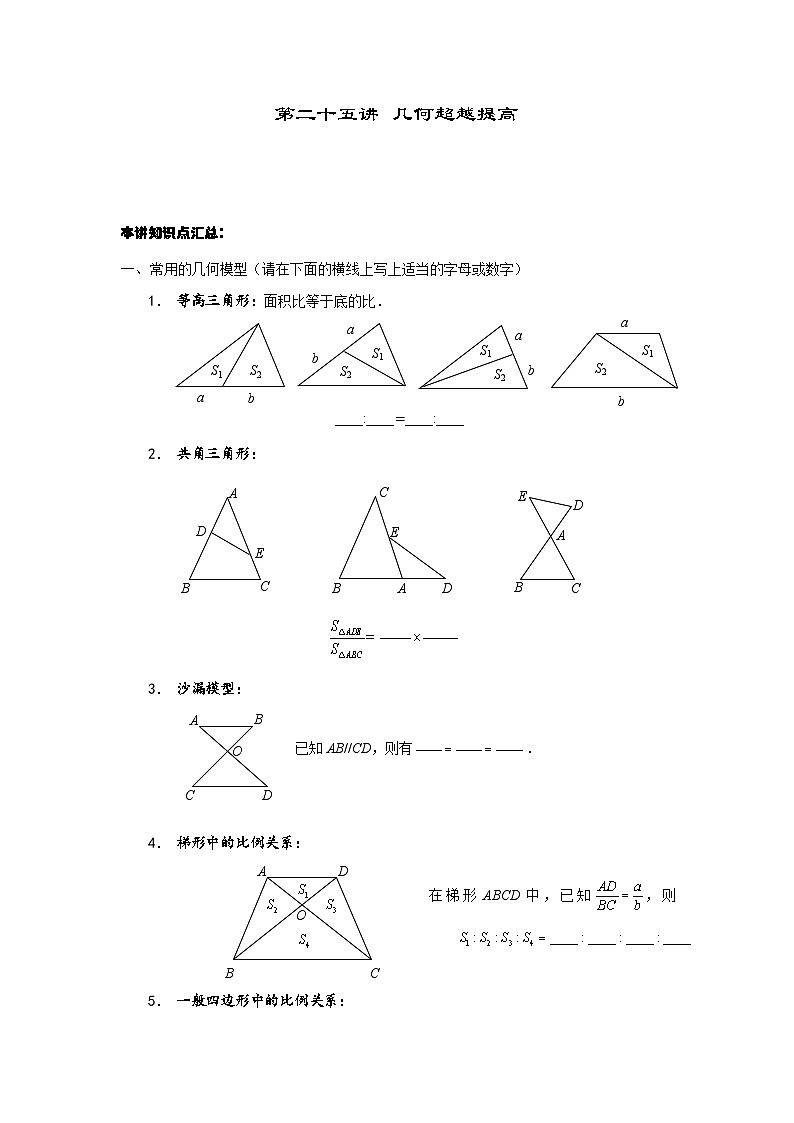
第二十五讲 几何超越提高   本讲知识点汇总：一、 常用的几何模型（请在下面的横线上写上适当的字母或数字）1．   等高三角形：面积比等于底的比．
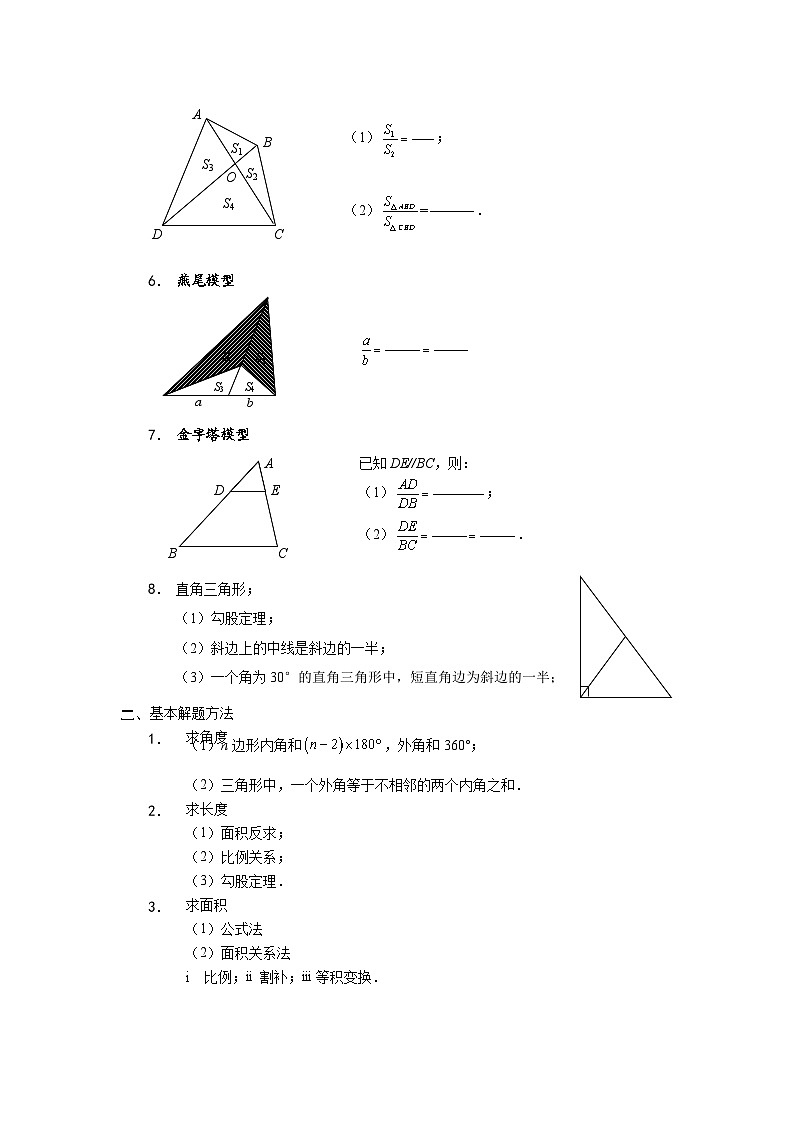
 2．   共角三角形：3．   沙漏模型： 4．   梯形中的比例关系：5．   一般四边形中的比例关系：6．   燕尾模型7．   金字塔模型8．   直角三角形；
（1）勾股定理；
（2）斜边上的中线是斜边的一半；
（3）一个角为30°的直角三角形中，短直角边为斜边的一半；二、 基本解题方法1．        求角度
（1）n边形内角和，外角和360°；
（2）三角形中，一个外角等于不相邻的两个内角之和．2．        求长度
（1）面积反求；
（2）比例关系；
（3）勾股定理．3．        求面积
（1）公式法
（2）面积关系法
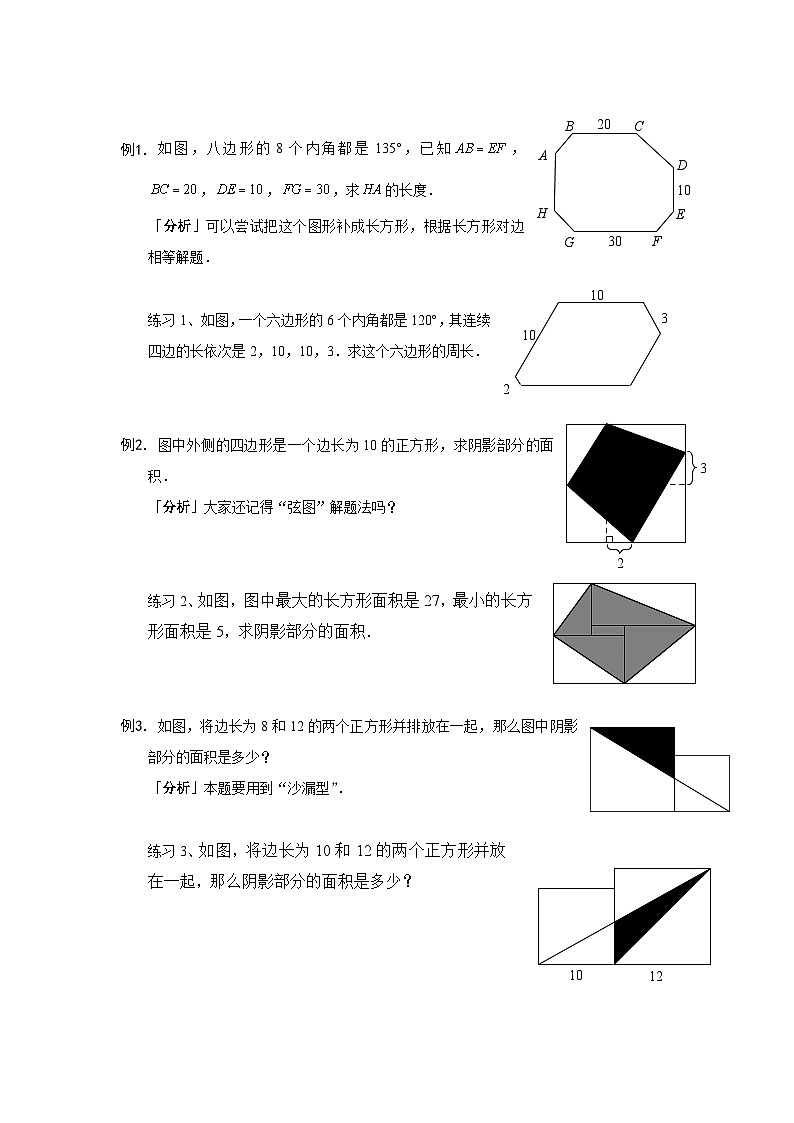
i 比例；ii 割补；iii 等积变换． 例1． 如图，八边形的8个内角都是135°，已知，，，，求的长度．「分析」可以尝试把这个图形补成长方形，根据长方形对边相等解题．
 练习1、如图，一个六边形的6个内角都是120，其连续四边的长依次是2，10，10，3．求这个六边形的周长．

 例2． 图中外侧的四边形是一个边长为10的正方形，求阴影部分的面积．
「分析」大家还记得“弦图”解题法吗？


练习2、如图，图中最大的长方形面积是27，最小的长方形面积是5，求阴影部分的面积．

 例3． 如图，将边长为8和12的两个正方形并排放在一起，那么图中阴影部分的面积是多少？
「分析」本题要用到“沙漏型”．

练习3、如图，将边长为10和12的两个正方形并放在一起，那么阴影部分的面积是多少？



 例4． 如图，△ABC是等腰直角三角形，DEFG是正方形，线段AB与CD相交于K点．已知正方形DEFG的面积是48，，则△BKD的面积是多少？
「分析」本题会巧妙的运用“等高三角形”解题．

练习4、如图，四边形ABCD是一个梯形，四边形ACEB是一个平行四边形．已知三角形BCE的面积是18，三角形AOD的面积是12，那么四边形ADEB的面积是多少？
 例5． 如图，边长为l的正方形ABCD中，，，三角形AEG的面积是多少？
「分析」这道题目需要做辅助线补成 “沙漏型”进行解题

 例6． 如图，长方形ABCD中，，，三角形DFG的面积为2，长方形ABCD的面积是多少？
「分析」这道题目也需要做辅助线解题．

 
印加文明南美洲古代印第安人文明．印加为其最高统治者的尊号，意为太阳之子．15世纪起势力强盛，极盛时期的疆界以今秘鲁和玻利维亚为中心，北抵哥伦比亚和厄瓜多尔，南达智利中部和阿根廷北部，首都在秘鲁南部的库斯科．16世纪初由于内乱日趋衰落，1532年被西班牙殖民者灭亡．印加文明与玛雅文明、阿兹特克文明并称为“印第安三大古老文明”．具有殖民征服者和印加帝国王室成员双重身份的印卡·加西拉索·德拉维加，对16、17世纪西班牙征服南美洲印第安文明的过程有着独特的关照视角，并始终保持着对这场新旧文明冲突的矛盾立场．印加文明是在南美洲西部、中安第斯山区发展起来的又一著名的印第安古代文明．它的影响范围北起哥伦比亚南部的安卡斯马约河、南到智利中部的马乌莱河，全长4800公里，东西最宽处500公里，总面积达90多万平方公里，人口超过1000万．大体说来，它包括了现今厄瓜多尔山区、秘鲁山区部分，玻利维亚高原地区、半个智利和阿根廷西北部地区．印加帝国享有“美洲的罗马”之称，它以有一套完整的国家体系而闻名于世．印加国是一个奴隶制国家，奴隶主阶级包括印加王、王室贵族、高级官吏和祭司．他们不从事生产劳动，过着奢侈的生活．印加王被称为太阳之子，神的化身，拥有至高无上的权力，独揽国家一切政治、军事和宗教大权．为了维护自己的统治，印加王建立了以中央集权为中心的政治制度，他以斯科为中心，通过各级官吏，牢牢地控制着全国．除了政权机构外，印加奴隶主还拥有一支20万人的训练有素的常备军队，用其对外扩张，对内镇压反叛力量．印加帝国还建立了严厉的司法制度，用来维护奴隶主阶级的利益．为了巩固自己的统治，印加王还采取了一些文化和经济措施．例如，对于那些刚被征服的地区，强行推广克丘亚语．再者，在全国大兴道路和驿站建设，以库斯科为中心，修建了条条道路通京城的交通网，以利于对边远地区的控制．印加帝国的灭亡在1532年，最后一任印加帝国国王阿达华巴，被西班牙殖民侵略者弗朗西斯克·皮泽洛处以死刑，结束了400年以上繁荣的帝国历史．今日印加帝国最著名的遗址为建在马丘峰和华伊纳峰之间的马丘比丘．
作业1．   如图，在三角形ABC中，，，已知三角形ABC面积是1，那么三角形ABO的面积是多少？2/5



 2．   图中是两个边长分别为8和12的正方形，那么阴影部分的面积是多少？
38.4



 3．   如图，在五边形中有一个角为60°，别的角都是120°．这个五边形的周长是多少？
14



 4．   如图，已知正方形ABCD的边长为20，E、F分别为AB及BC之中点．那么四边形BFGE的面积是多少？(80)






 5．   如图，在边长为20的正方形中，有一个四边形，那么阴影部分的面积是多少？
112