

2023-2024学年江苏省宿迁市沭阳县乡镇联考八年级(上)月考数学试卷(10月份)(含解析)
展开
这是一份2023-2024学年江苏省宿迁市沭阳县乡镇联考八年级(上)月考数学试卷(10月份)(含解析),共24页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
1.下面四个图形分别是节能、节水、低碳和绿色食品标志,在这四个标志中,是轴对称图形的是( )
A. B. C. D.
2.已知图中的两个三角形全等,则∠α的度数是( )
A. 72°B. 60°C. 58°D. 50°
3.下列说法正确的是( )
A. 形状相同的两个三角形全等B. 面积相等的两个三角形全等
C. 完全重合的两个三角形全等D. 全等三角形的周长和面积不相等
4.如图,点B在线段AD上,△ABC≌△EBD,AB=2cm,BD=5cm,则CE的长度为( )
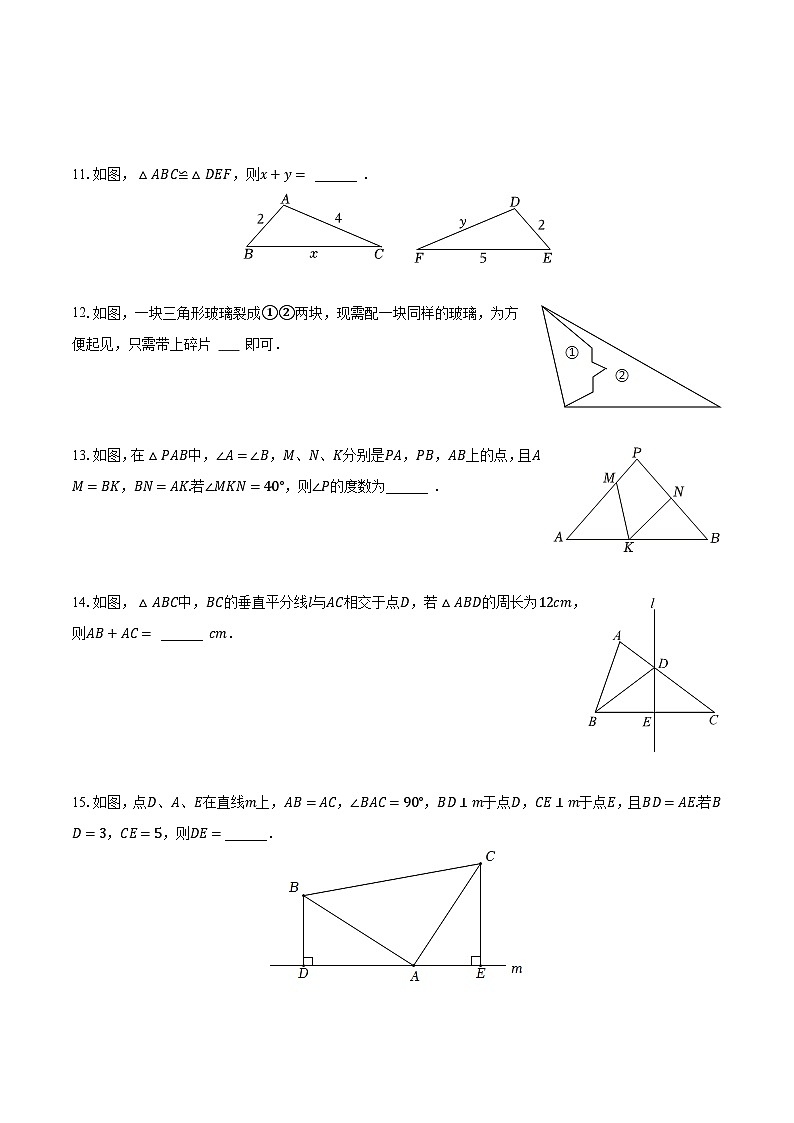
A. 2cm
B. 2.5cm
C. 3cm
D. 5cm
5.要测量圆形工件的外径,工人师傅设计了如图所示的卡钳,点O为卡钳两柄交点,且有OA=OB=OC=OD,如果圆形工件恰好通过卡钳AB,则此工件的外径必是CD之长了,其中的依据是全等三角形的判定条件
( )
A. SSSB. SASC. ASAD. AAS
6.如图,已知∠DAB=∠CAB,添加下列条件不能判定△DAB≌△CAB的是( )
A. ∠DBE=∠CBE
B. ∠D=∠C
C. DA=CA
D. DB=CB
7.如图,射线OC平分∠AOB,点D、Q分别在射线OC、OB上,若OQ=4,△ODQ的面积为10,过点D作DP⊥OA于点P,则DP的长为( )
A. 10
B. 5
C. 4
D. 3
8.如图,在5×5的正方形网格中,△ABC的三个顶点都在格点上,则与△ABC有一条公共边且全等(不与△ABC重合)的格点三角形(顶点都在格点上的三角形)共有( )
A. 5个
B. 6个
C. 7个
D. 8个
二、填空题(本大题共10小题,共30.0分)
9.如图,∠D=∠C=90°,请你再添加一个条件,使△ABD≅△ABC,你添加的条件是______ .
10.如图,在4×4网格中,∠1+∠2= ______ .
11.如图,△ABC≌△DEF,则x+y= ______ .
12.如图,一块三角形玻璃裂成①②两块,现需配一块同样的玻璃,为方便起见,只需带上碎片 即可.
13.如图,在△PAB中,∠A=∠B,M、N、K分别是PA,PB,AB上的点,且AM=BK,BN=AK.若∠MKN=40°,则∠P的度数为______ .
14.如图,△ABC中,BC的垂直平分线l与AC相交于点D,若△ABD的周长为12cm,则AB+AC= ______ cm.
15.如图,点D、A、E在直线m上,AB=AC,∠BAC=90°,BD⊥m于点D,CE⊥m于点E,且BD=AE.若BD=3,CE=5,则DE=______.
16.如图,△ABC≌△DEF,则此图中相等的线段有______对.
17.如图,AB=CB,AD=CD,连AC,BD交于点O,下面四个结论:
①△ABD≌△CBD;
②AC⊥BD;
③AC=BD;
④AO=CO,
其中正确结论的序号为______ .
18.已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°:③AD=AE=EC;④AC+BC=2BF.其中正确的是______ .(只填序号)
三、解答题(本大题共10小题,共96.0分。解答应写出文字说明,证明过程或演算步骤)
19.(本小题8.0分)
如图,AB=AD,AC=AE,△ABC与△ADE全等吗?为什么?
20.(本小题8.0分)
如图,在边长为1个单位长度的小正方形组成的10×10的网格中,给出了格点(顶点为网格线的交点)△ABC,l是过网格线的一条直线.
(1)求△ABC的面积;
(2)作△ABC关于直线l对称的图形△A′B′C′;
(3)在边BC上找一点D,连接AD,使得∠BAD=∠ABD.(保留作图痕迹)
21.(本小题8.0分)
如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF.求证:AD平分∠BAC.
22.(本小题10.0分)
如图,点A,B,C,D在同一条直线上,点E,F分别在直线AB的两侧,且AE=BF,∠A=∠B,∠ACE=∠BDF.
(1)求证:△ACE≌△BDF;
(2)若AB=8,AC=2,求CD的长.
23.(本小题10.0分)
如图,点B、E、C、F在一条直线上,AB=DE,AC=DF,BE=CF.
(1)求证:△ABC≌△DEF;
(2)若∠D=45°,求∠EGC的大小.
24.(本小题10.0分)
如图,在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G.
(1)若BC=10,求△AEG的周长;
(2)若∠BAC=120°,求∠EAG的度数.
25.(本小题10.0分)
如图,AD与BC相交于点O,OA=OC,∠A=∠C,BE=DE.
(Ⅰ)求证:OB=OD;
(Ⅱ)求证:OE垂直平分BD.
26.(本小题8.0分)
如图,小刚站在河边的点A处,在河对面(小刚的正北方向)的点B处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30步到达一棵树C处,接着再向前走了30步到达D处,然后他左转90°直行,从点D处开始计步,当小刚看到电线塔、树与自己现处的位置E在一条直线时,他恰好走了80步,并且小刚一步大约0.5米.由此小刚估计出了在点A处时他与电线塔的距离,请问他的做法是否合理?若合理,请求出在点A处时他与电线塔的距离;若不合理,请说明理由.
27.(本小题12.0分)
如图,四边形ABCD中,BC=CD,AC=DE,AB//CD,∠B=∠DCE=90°,AC与DE相交于点F.
(1)求证:△ABC≌△ECD;
(2)判断线段AC与DE的位置关系,并说明理由.
28.(本小题12.0分)
如图①,在Rt△ABC中,∠C=90°,BC=9cm,AC=12cm,AB=15cm,现有一动点P,从点A出发,沿着三角形的边AC→CB→BA运动,回到点A停止,速度为3cm/s,设运动时间为ts.
(1)如图(1),当t=______时,△APC的面积等于△ABC面积的一半;
(2)如图(2),在△DEF中,∠E=90°,DE=4cm,DF=5cm,∠D=∠A.在△ABC的边上,若另外有一个动点Q,与点P同时从点A出发,沿着边AB→BC→CA运动,回到点A停止.在两点运动过程中的某一时刻,恰好△APQ≌△DEF,求点Q的运动速度.
答案和解析
1.【答案】B
【解析】解:选项A、C、D的图形不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形.
选项B的图形能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形.
故选:B.
根据如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.
本题考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
2.【答案】A
【解析】解:∵图中的两个三角形全等,
∴b与b,c与c分别是对应边,那么它们的夹角就是对应角,
∴∠α=72°.
故选:A.
要根据已知的对应边去找对应角,并运用“全等三角形对应角相等”即可得答案.
本题考查全等三角形的性质,熟知全等三角形的对应角相等是解题的关键.
3.【答案】C
【解析】解:A.形状相同,边长不对应相等的两个三角形不全等,故本选项错误;
B.面积相等的两个三角形不一定全等,故本选项错误;
C.完全重合的两个三角形全等,正确;
D.全等三角形的周长和面积相等,故本选项错误;
故选:C.
根据三角形全等的判定定理进行解答即可.
本题考查的是三角形全等的判定,熟知三角形的性质及全等判定定理是解答此题的关键.
4.【答案】C
【解析】解:∵△ABC≌△EBD,
∴BE=AB=2cm,BC=BD=5cm,
∴CE=BC−BE=5cm−2cm=3cm,
故选:C.
根据全等三角形的对应边相等,再利用线段和差即可求解.
此题考查了全等三角形的性质,解题的关键熟练掌握性质的应用.
5.【答案】B
【解析】【分析】
本题考查了全等三角形的应用,熟练掌握三角形全等的判定方法是解题的关键.
连接AB、CD,然后利用“边角边”证明△ABO和△DCO全等,根据全等三角形对应边相等解答.
【解答】
解:如图,连接AB、CD,
在△ABO和△DCO中,OA=OD∠AOB=∠DOCOB=OC,
∴△ABO≌△DCO(SAS),
∴AB=CD.
故选:B.
6.【答案】D
【解析】解:A.添加∠DBE=∠CBE,根据三角形外角的性质,得∠D=∠DBE−∠DAB,∠C=∠EBC−∠CAB,那么∠D=∠C,从而根据AAS判定△DAB≌△CAB,故A不符合题意.
B.添加∠D=∠C,根据AAS判定△DAB≌△CAB,故B不符合题意.
C.添加DA=CA,根据SAS判定△DAB≌△CAB,故C不符合题意.
D.添加DB=CB,无法判定△DAB≌△CAB,故D符合题意.
故选:D.
根据全等三角形的判定方法(SSS、SAS、AAS、ASA)解决此题.
本题主要考查全等三角形的判定,熟练掌握全等三角形的判定方法是解决本题的关键.
7.【答案】B
【解析】解:过点D作DE⊥OB,垂足为E,
∵OQ=4,△ODQ的面积为10,
∴12OQ⋅DE=10,
∴DE=5,
∵射线OC平分∠AOB,DE⊥OB,DP⊥OA,
∴DE=DP=5,
故选:B.
过点D作DE⊥OB,垂足为E,先根据三角形的面积求出DE的长,然后利用角平分线的性质可得DE=DP=5,即可解答.
本题考查了角平分线的性质,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
8.【答案】B
【解析】解:如图所示,
以BC为公共边可画出△BDC,△BEC,△BFC三个三角形和原三角形全等.
以AB为公共边可画出△ABG,△ABM,△ABH三个三角形和原三角形全等.
以AC为公共边不可以画出一个三角形和原三角形全等,
所以可画出6个.
故选:B.
根据全等三角形的判定分别求出以AB为公共边的三角形,以CB为公共边的三角形,以AC为公共边的三角形的个数,相加即可.
本题考查全等三角形的判定,三条边分别相等的两个三角形全等,以及格点的概念,熟练掌握全等三角形的判定定理是解决问题的关键.
9.【答案】∠CAB=∠DAB(本题答案不唯一)
【解析】解:添加的条件:∠CAB=∠DAB或∠CBA=∠DBA,此时△ABD≅△ABC(AAS);
添加的条件:AC=AD或BC=BD,此时△ABD≅△ABC(HL);
故答案为:∠CAB=∠DAB(本题答案不唯一).
已知∠D=∠C=90°,图形条件AB=AB,可以从角,边两方面添加条件.
本题考查了全等三角形的判定.关键是根据题目的已知条件,图形条件,合理地选择判定方法.
10.【答案】45°
【解析】解:由题意得,CA=FD= 13,CB=FE=1,AB=DE=2 2,
在△CAB和△FDE中,
CA=FDCB=FEAB=DE,
∴△CAB≌△FDE(SSS),
∴∠1=∠DFE,
∵∠2+∠DFE=∠DEG=45°,
∴∠1+∠2=45°,
故答案为:45°.
由题意得,CA=FD,AB=DE,CB=FE,用SSS可证明△CAB≌△FDE,根据全等三角形的性质和外角和内角之间的关系即可得.
本题考查了全等三角形的判定与性质,三角形的外角与内角的关系,解题的关键是掌握全等三角形的判定与性质.
11.【答案】9
【解析】解:∵△ABC≌△DEF,
∴BC=FE=5,DF=AC=4,
∴x=5,y=4,
∴x+y
=5+4
=9.
故答案为:9.
由全等三角形的性质,得到x=5,y=4,即可求出x+y的值.
本题考查全等三角形的性质,关键是掌握全等三角形的性质:全等三角形的对应边相等.
12.【答案】②
【解析】解:②中满足两边夹一角完整,即可得到一个与原来三角形全等的新三角形,所以只需带②去即可.
故答案是:②.
此题实际上考查全等三角形的应用,②中两边及其夹角,进而可确定其形状.
本题考查了三角形全等的应用;能够灵活运用全等三角形的判定,解决一些实际问题,注意认真读图.
13.【答案】100°
【解析】解:在△MAK和△KBN中,
AM=BK∠A=∠BAK=BN,
∴△MAK≌△KBN(SAS),
∴∠BKN=∠AMK,
∵∠MKB是△AMK的外角,
∴∠BKN+∠MKN=∠A+∠AMK,
∴∠A=∠MKN=40°,
∴∠B=∠A=40°,
∴∠P=180°−40°−40°=100°,
故答案为:100°.
证明△MAK≌△KBN,根据全等三角形的性质得到∠BKN=∠AMK,根据三角形的外角性质求出∠A,根据三角形内角和定理计算,得到答案.
本题考查的是全等三角形的判定和性质、三角形的外角性质、三角形内角和定理,掌握全等三角形的判定定理是解题的关键.
14.【答案】12
【解析】解:∵l是BC的垂直平分线,
∴DB=DC,
∵△ABD的周长为12cm,
∴AB+AD+BD=12cm,
∴AB+AD+DC=12cm,
∴AB+AC=12cm,
故答案为:12.
根据线段垂直平分线的性质可得DB=DC,然后根据三角形的周长可得AB+AD+BD=12cm,从而可得AB+AD+DC=12cm,进而可得AB+AC=12cm,即可解答.
本题考查了线段垂直平分线的性质,熟练掌握线段垂直平分线的性质是解题的关键.
15.【答案】8
【解析】解:∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠CEA=90°,
∴∠BAD+∠ABD=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∴∠CAE=∠ABD,
∵在△ADB和△CEA中,
∠BDA=∠CEA ∠ABD=∠CAE AB=AC ,
∴△ADB≌△CEA(AAS),
∴BD=AE=3,AD=CE=5,
∴DE=AD+AE=8,
故答案为:8.
根据BD⊥直线m,CE⊥直线m得∠BDA=∠CEA=90°,而∠BAC=90°,根据等角的余角相等得∠CAE=∠ABD,然后根据“AAS”可判断△ADB≌△CEA,根据全等三角形的性质即可得解.
此题考查了全等三角形的判定与性质,根据“AAS”判断△ADB≌△CEA是解题的关键.
16.【答案】4
【解析】解:∵△ABC≌△DEF,
∴AB=DE,AC=DF,BC=EF,
又∵BE=BC−EC,CF=EF−EC,
∴CF=BE,
∴相等的线段有:AB=DE,AC=DF,BC=EF,CF=BE,共4对.
故答案为:4.
根据全等三角形对应边相等解答即可.
本题考查了全等三角形对应边相等的性质,结合图形准确找出对应边是解题的关键.
17.【答案】①②④
【解析】解:在△ADB和△CDB中,
AB=CBAD=CDBD=BD,
∴△ADB≌△CDB(SSS),故①正确;
∵AB=CB,AD=CD,
∴BD是AC的垂直平分线,
∴AC⊥BD,故②④正确;
但是AC不一定等于BD,故③错误,
综上所述:正确结论的序号为:①②④;
故答案为:①②④.
根据全等三角形的性质和判定解答即可.
本题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定方法是解题的关键.
18.【答案】①②③
【解析】解:①∵BD为△ABC的角平分线,
∴∠ABD=∠CBD,
在△ABD和△EBC中,
BD=BC∠ABD=∠CBDBE=BA,
∴△ABD≌△EBC(SAS),
∴①正确;
②∵BD为△ABC的角平分线,BD=BC,BE=BA,
∴∠BCD=∠BDC,∠BAE=∠BEA,
∵△ABD≌△EBC,
∴∠BCE=∠BDA,
∴∠BCE+∠BCD=∠BDA+∠BDC=180°,
∴②正确;
③∵BC=BD,BE=BA,
∴∠BCD=∠BDC,∠BEA=∠BAE,
∵∠CAD=∠ABE,
∴∠BCD=∠BEA,
∵∠BCE=∠BDA,∠BCE=∠BCD+∠DCE,∠BDA=∠DAE+∠BEA,
∴∠DCE=∠DAE,
∴△ACE为等腰三角形,
∴AE=EC,
∵△ABD≌△EBC,
∴AD=EC,
∴AD=AE=EC,
∴③正确;
④过E作EG⊥BC于G点,
∵E是∠ABC平分线BD上的点,EF⊥AB,
∴EF=EG,
在Rt△BEG和Rt△BEF中,
BE=BEEF=EG,
∴Rt△BEG≌Rt△BEF(HL),
∴BG=BF,
在Rt△CEG和Rt△AFE中,
EF=EGAE=CE,
∴Rt△CEG≌Rt△AEF(HL),
∴AF=CG,
∴BA+BC=BF+FA+BG−CG=BF+BG=2BF,
但AB≠AC,
∴AC+BC=2BF错误.
故④不正确.
综上所述,正确的结论是①②③.
故答案为:①②③.
利用SAS证明△ABD≌△EBC,可判断①正确;利用△ABD≌△EBC和等腰三角形性质可判断②正确;根据角平分线的性质和等腰三角形的性质可求得∠DAE=∠DCE,即可得到AD=AE=EC,可得③正确;由已知条件可得到AB+BC=2BF,但AC≠AB,可判断④不正确.
本题考查全等三角形的判定与性质,熟练证明三角形全等和熟练运用全等三角形对应角、对应边相等性质是解题的关键.
19.【答案】解:△ABC≌△ADE.
理由:在△ABC和△ADE中,
AB=AD∠BAC=∠DAEAC=AE,
所以△ABC≌△ADE(SAS).
【解析】根据全等三角形的判定定理求解即可.
本题主要考查三角形全等,牢固掌握三角形判定定理是解题关键.
20.【答案】解:(1)△ABC的面积=12×4×5=10;
(2)如图,△A′B′C′即为所求;
(3)如图,点D即为所求.
【解析】(1)直接利用三角形的面积公式计算即可;
(2)利用网格特点和轴对称的性质画出A、B、C关于直线l的对称点,再顺次连接即可得到△A′B′C′;
(3)利用网格特点得到AB的垂直平分线与BC的交点为D点.
本题考查了作图−轴对称变换:几何图形都可看作是由点组成,我们在画一个图形的轴对称图形时,也是先从确定一些特殊的对称点开始的.
21.【答案】证明:∵DE⊥AB,DF⊥AC,
∴∠E=∠DFC=90°,
在Rt△BDE和Rt△CDF中,
BD=CDBE=CF,
∴Rt△BDE≌Rt△CDF(HL),
∴DE=DF,
∴AD平分∠BAC.
【解析】此题考查了角平分线的判定与全等三角形的判定与性质,属于基础题.
由DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF,即可判定Rt△BDE≌Rt△CDF(HL),则可得DE=DF,然后由角平分线的判定定理,即可证得AD平分∠BAC.
22.【答案】(1)证明:在△ACE和△DBF中,
∠A=∠B∠ACE=∠BDFAE=BF,
∴△ACE≌△DBF(AAS);
(2)由(1)知△ACE≌△BDF,
∴BD=AC=2,
∵AB=8,
∴CD=AB−AC−BD=4,
故CD的长为4.
【解析】(1)根据全等三角形的判定定理证明△ACE≌△DBF即可;
(2)根据全等三角形的性质即可得到结论.
此题主要考查了全等三角形的判定与性质;熟练掌握证明三角形全等是解决问题的关键.
23.【答案】(1)证明:∵BE=CF,
∴BE+EC=CF+EC,
∴BC=EF,
在△ABC和△DEF中,
AB=DEAC=DFBC=EF,
∴△ABC≌△DEF(SSS);
(2)解:∵△ABC≌△DEF,∠D=45°,
∴∠A=∠D=45°,∠B=∠DEF,
∴AB//DE,
∴∠EGC=∠A=45°.
【解析】(1)根据线段的和差证出BC=EF,由SSS即可得出△ABC≌△DEF;
(2)由全等三角形的性质得到∠A=∠D=45°,∠B=∠DEF,根据平行线的判定与性质即可得解.
此题考查了全等三角形的判定与性质,由SSS得出△ABC≌△DEF是解题的关键.
24.【答案】解:(1)∵DE是AB的垂直平分线,GF是AC的垂直平分线,
∴EA=EB,GA=GC,
∴△AEG的周长=EA+EG+GA=EB+EG+GC=BC=10;
(2)∵∠BAC=120°,
∴∠B+∠C=180°−120°=60°,
∵EA=EB,GA=GC,
∴∠EAB=∠B,∠GAC=∠C,
∴∠EAB+∠GAC=∠B+∠C=60°,
∴∠EAG=120°−60°=60°.
【解析】(1)利用DE是AB的垂直平分线,GF是AC的垂直平分线,得到EA=EB,GA=GC,即可得出答案;
(2)利用三角形内角和得出∠B+∠C=60°,由EA=EB,GA=GC得出∠EAB=∠B,∠GAC=∠C,继而得出∠EAB+∠GAC=∠B+∠C=60°,得出∠EAG=60°.
本题考查线段垂直平分线性质,掌握线段垂直平分线性质是解题关键.
25.【答案】证明:(Ⅰ)在△AOB和△COD中,
∠A=∠CAO=CO∠AOB=∠COD,
∴△AOB≌△COD(ASA),
∴OB=OD.
(Ⅱ)∵OB=OD,EB=ED,
∴OE垂直平分线段BD.
【解析】(Ⅰ)证明△AOB≌△COD(SAS),可得结论.
(Ⅱ)根据线段的垂直平分线的判定解决问题即可.
本题考查全等三角形的判定和性质,线段的垂直平分线的判定等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.
26.【答案】解:合理.理由如下:
根据题意,得AC=DC.
在△ABC和△DEC中,
∠A=∠DAC=DC∠ACB=∠DCE,
∴△ABC≌△DEC(ASA).
∴AB=DE.
又∵小刚走完DE用了80步,一步大约0.5米,
∴AB=DE=80×0.5=40(米).
答:小刚在点A处时他与电线塔的距离为40米.
【解析】合理.理由:通过ASA证得△ABC≌△DEC(ASA),则其对应边相等AB=DE.结合速度×时间=距离求得点A处时他与电线塔的距离即可.
本题考查全等三角形的应用,在实际生活中,对于难以实地测量的线段,常常通过两个全等三角形,转化需要测量的线段到易测量的边上或者已知边上来,从而求解.
27.【答案】(1)证明:在Rt△ABC和Rt△ECD中,
AC=DEAB=EC,
∴Rt△ABC≌Rt△ECD(HL),
(2)解:AC⊥DE.理由如下:
∵△ABC≌△ECD,
∴∠BCA=∠CDE,
∵∠B=∠DCE=90°,
∴∠BCA+∠ACD=90°,
∴∠CDE+∠ACD=90°,
∴∠DFC=180°−(∠CDE+∠ACD)=90°,
∴AC⊥DE.
【解析】(1)根据HL即可证明△ABC≌△ECD.
(2)根据△ABC≌△ECD得到∠BCA=∠CDE,结合∠B=∠DCE=90°得到∠DFC=90°,即可得结论.
本题考查全等三角形的判定与性质,常用的判定方法有:SSS、SAS、ASA、AAS、HL等,熟练掌握全等三角形的判定定理是解题的关键.
28.【答案】解:(1)112或192;
(2)△APQ≌△DEF,即对应顶点为A与D,P与E,Q与F.
①当点P在AC上,如图②−1所示:
此时,AP=4,AQ=5,
∴点Q移动的速度为5÷(4÷3)=154cm/s;
②当点P在AB上,如图②−2所示:
此时,AP=4,AQ=5,
即点P移动的距离为9+12+15−4=32cm,点Q移动的距离为9+12+15−5=31cm,
∴点Q移动的速度为31÷(32÷3)=9332cm/s,
综上所述,两点运动过程中的某一时刻,恰好△APQ≌△DEF,点Q的运动速为154cm/s或9332cm/s.
【解析】【分析】
本题考查直角三角形的性质,全等三角形的判定,画出相应图形,求出各点移动的距离是正确解答的关键.
(1)分两种情况进行解答,①当点P在BC上时,②当点P在BA上时,分别画出图形,利用三角形的面积之间的关系,求出点P移动的距离,从而求出时间即可;
(2)由△APQ≌△DEF,可得对应顶点为A与D,P与E,Q与F;于是分两种情况进行解答,①当点P在AC上,②当点P在AB上,分别求出P移动的距离和时间,进而求出Q的移动速度.
【解答】
解:(1)①当点P在BC上时,如图①−1,
若△APC的面积等于△ABC面积的一半,则CP=12BC=92cm,
此时,点P移动的距离为AC+CP=12+92=332,
移动的时间为:332÷3=112秒;
②当点P在BA上时,如图①−2,
若△APC的面积等于△ABC面积的一半,则PD=12BC,即点P为BA中点,
此时,点P移动的距离为AC+CB+BP=12+9+152=572cm,
移动的时间为:572÷3=192秒,
故答案为:112或192;
(2)见答案.
相关试卷
这是一份2023-2024学年江苏省宿迁市沭阳县怀文中学七年级(上)分班考数学试卷(含解析),共10页。试卷主要包含了选择题,填空题,5个十分之一,解答题等内容,欢迎下载使用。
这是一份2023-2024学年江苏省宿迁市沭阳县八年级(上)期中数学试卷,共22页。试卷主要包含了选择题等内容,欢迎下载使用。
这是一份2023-2024学年江苏省宿迁市沭阳县五校联考七年级(上)期中数学试卷(含解析),共4页。试卷主要包含了单选题,填空题,计算题,应用题等内容,欢迎下载使用。









