甘肃省武威市古浪县黄羊川九年一贯制学校2022-2023 学年上学期九年级数学期末测试卷

这是一份甘肃省武威市古浪县黄羊川九年一贯制学校2022-2023 学年上学期九年级数学期末测试卷，共15页。试卷主要包含了3 的相反数是，下列说法不正确的是，满足一次函数关系，并且当 x等内容，欢迎下载使用。
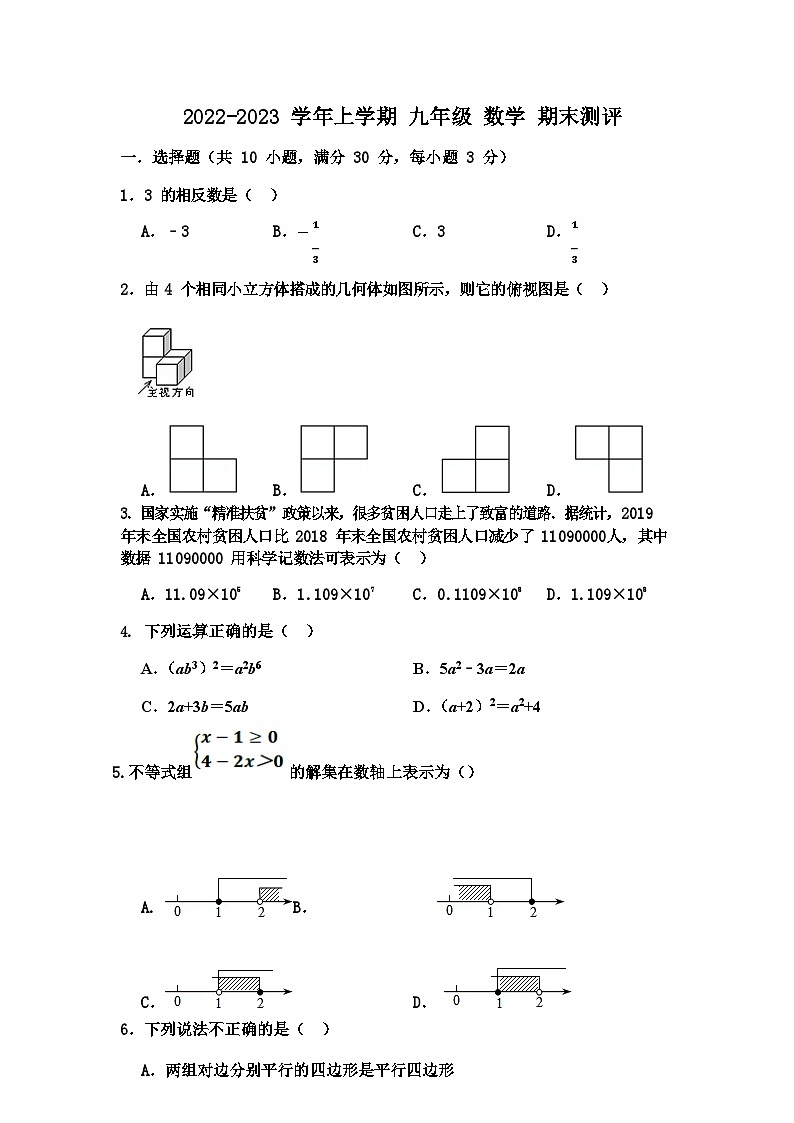
2022-2023 学年上学期 九年级 数学 期末测评 一．选择题（共 10 小题，满分 30 分，每小题 3 分） 1．3 的相反数是（ ） A．﹣3 B．− ? C．3 D．? ? ?2．由 4 个相同小立方体搭成的几何体如图所示，则它的俯视图是（ ）
A．  B．  C．  D．  3．国家实施“精准扶贫”政策以来，很多贫困人口走上了致富的道路．据统计，2019 年末全国农村贫困人口比 2018 年末全国农村贫困人口减少了 11090000人，其中数据 11090000 用科学记数法可表示为（ ） A．11.09×105 B．1.109×107 C．0.1109×108 D．1.109×108 下列运算正确的是（ ） A．（ab3）2＝a2b6 B．5a2﹣3a＝2aC．2a+3b＝5ab D．（a+2）2＝a2+4
 
5.不等式组            的解集在数轴上表示为（）   B．   C．  D． 6．下列说法不正确的是（ ） A．两组对边分别平行的四边形是平行四边形B．有一个角是直角的平行四边形是矩形  C．对角线互相垂直的四边形是菱形      D．对角线相等的菱形是正方形7．如图，把一块含有 45°的直角三角形的两个顶点放在直尺的对边上，若∠1＝20°，则∠2 的度数是（ ）
A．15° B．20° C．25° D．30°        第 7 题 图                               第 8 题 图 如图，在已知的△ABC 中，按以下步骤作图：①分别以 B，C 为圆心，以大于? BC 的长为半径作弧，两弧相交于两点 M，N；②作直线 MN 交 AB 于点? D，连接 CD．若 CD＝AC，∠A＝50°，则∠ACB 的度数为（ ） A．105° B．100°       C．95°              D．90° 已知抛物线 y＝ax2+bx+c 的图象如图所示，则下列结论中，正确的有（ ） ①abc＞0；②b2＞4ac；③a﹣b+c＜0； ⑤a+c＜1．                          第 9 题 图             第 10 题 图 A．1 个 B．2 个 C．3 个 D．4 个 如图，AC 为矩形 ABCD 的对角线，已知 AD＝3，CD＝4，点 P 沿折线 C﹣A﹣D 以每秒 1 个单位长度的速度运动（运动到 D 点停止），过点 P 作 PE⊥BC于点 E，则△CPE 的面积 y 与点 P 运动的路程 x 间的函数图象大致是（    ）      A．  B． 
      C．  D．  二．填空题（共 5 小题，满分 15 分，每小题 3 分） 关于 x 的方程 x2﹣4x+m＝0 有一个根为﹣1，则另一个根为       ． 如图，AD∥BE∥CF，AB＝3，BC＝6，DE＝2，则 EF 的值为      ．


 第 12 题 图             第 13 题 图          第 14 题 图 如图，一个游戏转盘中，红、黄、蓝三个扇形的圆心角度数分别为 60°，90°，210°．让转盘自由转动，则指针停止后落在黄色区域的概率是     ． 如图，在△ABC 中，点 D，E，F 分别在 AB，AC，BC 上，DE∥BC，EF∥AB．若 AB=8，BD=3，BF=4，则 FC 的长为    _．   如图，四边形 ABCD 是边长为 4 的正方形，若 AF＝3，E 为 AB 上一个动点，把△AEF 沿着 EF 折叠，得到△PEF，若△BPE 为直角三角形，则 BP 的长度为        ．     
三．解答题（共 8 小题，满分 75 分） 16．（8 分） （1）计算：  （2）先化简，再求值：                      其中                        
             
17．（8 分）为引导学生知史爱党、知史爱国，某中学组织全校学生进行“党史知识“竞赛，该校德育处随机抽取部分学生的竞赛成绩进行统计，将成绩分为四个等级：优秀、良好、一般、不合格，并绘制成两幅不完整的统计图． 根据以上信息，解答下列问题：            （1）  德育处一共随机抽取了      名学生的竞赛成绩；在扇形统计图中， 表示“一般”的扇形圆心角的度数为 ； （2）  将条形统计图补充完整； （3）  该校共有 1400 名学生，估计该校大约有多少名学生在这次竞赛中成绩优秀？
18．（8 分）如图，在△ABC 中，AD 是 BC 边上的中线，点 E 是 AD 的中点，过点 A 作 AF∥BC 交 BE 的延长线于 F，连接 CF． （1）  求证：△AEF≌△DEB； （2）  当∠BAC＝    °时，四边形 ADCF 是菱形．        19．（9 分）本学期小明经过一段时间的学习，想利用所学的数学知识对某小区居民楼 AB 的高度进行测量．如图，先测得居民楼 AB 与 CD 之间的距离 BD 为 31m，后站在 F 点处测得居民楼 CD 的顶端 C 的仰角为 45°．居民楼 AB 的顶端 A 的仰角为 55°．已知居民楼 CD 的高度为 16.7m，小莹的观测点 E 距地面 1.7m．求居民楼 AB 的高度（精确到 1m）．（参考数据：sin55°≈0.82， cos55°≈0.57，tan55°≈1.43）
20．（10 分）某商家销售一种成本为 20 元的商品，销售一段时间后发现，每天的销量 y（件）与当天的销售单价 x（元/件）满足一次函数关系，并且当 x＝25 时，y＝550；当 x＝30 时 y＝500．物价部门规定，该商品的销售单价不能超过 52 元/件． （1）  求出 y 与 x 的函数关系式； （2）  问销售单价定为多少元时，商家销售该商品每天获得的利润是 8000 元？ （3）  当销售单价定为多少元时，商家销售该商品每天获得的利润最大，并求出最大利润．          21．（10分）如图，一次函数 y=  ?  x+b 的图象交反比例函数 y= ?的图象于点 A? ?和点 B，交 y 轴于点 C．  （1）  求反比例函数的解析式； （2）  求点 B 的坐标，并结合图象写出不等式                      的解集； （3）  点 P 在反比例函数 y= ?的图象上，且在直线 AB 下方，若 OP＝OB，请?直接写出点 P 的坐标．
22.（11 分）2021 年东京奥运会，中国跳水队赢得 8 个项目中的 7 块金牌，优异成绩的取得离不开艰辛的训练．某跳水运动员在进行跳水训练时，身体（看成一点）在空中的运动路线是如图所示的一条抛物线，已知跳板 AB 长为 2 米，跳板距水面 CD 的高 BC 为 3 米，训练时跳水曲线在离起跳点水平距离 1 米时达到距水面最大高度 k 米，现以 CD 为横轴，CB 为纵轴建立直角坐标系． （1）  当 k＝4 时，求这条抛物线的解析式．  （2）  当 k＝4 时，求运动员落水点与点 C 的距离．  （3）  图中      米 ， CF＝5 米，若跳水运动员在区域 EF 内（含点 E，F）入水时才能达到训练要求，求 k 的取值范围．           
23．（11 分）在学习全等三角形知识时，数学兴趣小组发现这样一个模型：模型是由两个顶角相等且有公共顶角顶点的等腰三角形组成的图形，如果把它们的底角顶点连接起来，则在相对位置变化的过程中，始终存在一对全等三角形，我们把这种模型称为“手拉手模型”．这个数学兴趣小组进行了如下操作： （1）  如图 1、两个等腰直角三角形△ABC 和△ADE 中，AB＝AC，AE＝AD，∠BAC＝∠DAE＝90°，连接 BD，CE，两线交于点 P，和△ABD 全等的三角形是 ，BD 和 CE 的数量关系是 ． （2）  如图 2，点 P 是线段 AB 上的动点，分别以 AP，BP 为边在 AB 的同侧作正方形 APCD 与正方形 PBEF，连接 DE 分别交线段 BC，PC 于点 M，N． ①求∠DMC 的度数； ②连接 AC 交DE 于点H，直接写出            的值．  （3）  如图 3，已知点 C 为线段 AE 上一点，AE＝8cm，△ABC 和△CDE 为AE 同侧的两个等边三角形，连接 BE 交 CD 于 N，连接 AD 交 BC 于 M，连接 MN，线段 MN 的最大值是 ．