江苏省无锡市太湖格致中学2023-2024学年九年级上学期10月阶段性练习数学试卷（月考）

这是一份江苏省无锡市太湖格致中学2023-2024学年九年级上学期10月阶段性练习数学试卷（月考），共6页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
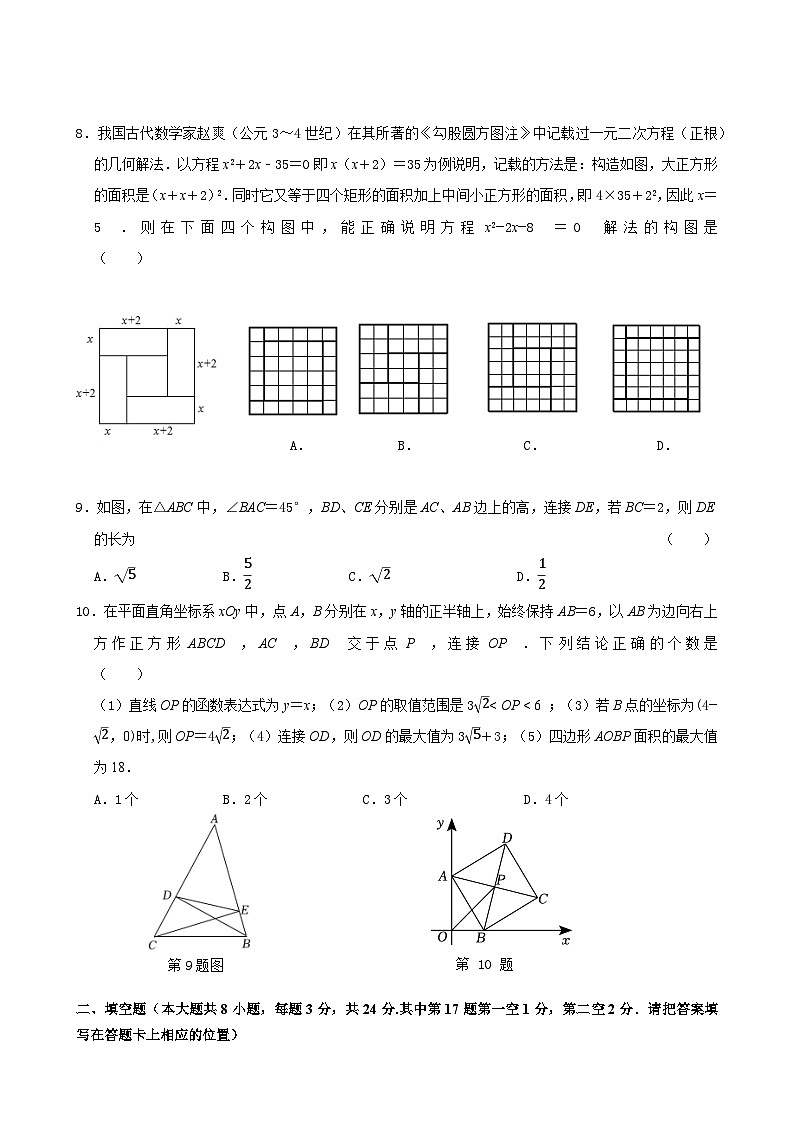
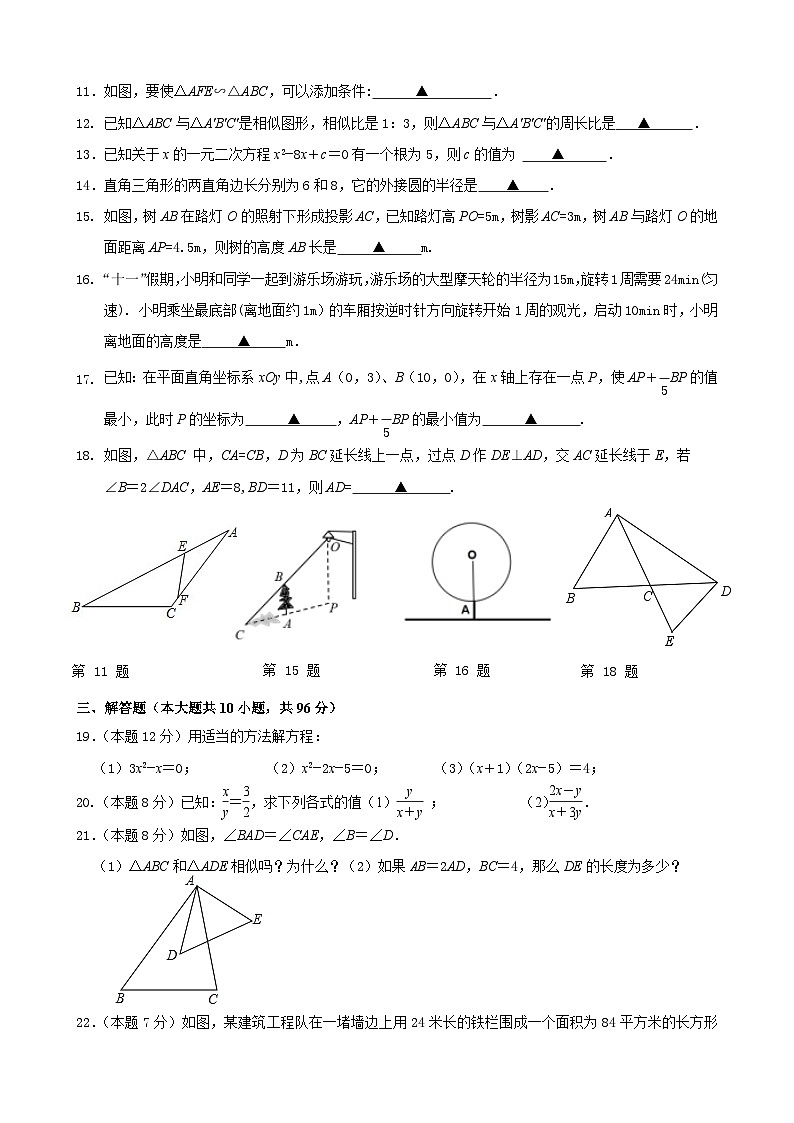
初三数学阶段性练习（2023.10）（满分150分，考试时间120分钟）一、选择题（本大题共10小题，每小题3分，共30分.在每小题所给出的四个选项中，只有一项是正确的，请用2B铅笔把答题卡上相应的选项标号涂黑）1．下列方程中，是一元二次方程的是                                                    （    ）A．x2＋3x＋y＝0     B．x＋y＋1＝0      C．x2＝0         D．x2＋＋5＝02．已知⊙O的半径为3，当OP＝5时，点P与⊙O的位置关系为                            （    ）A．点在圆内          B．点在圆外         C．点在圆上     D．不能确定3．把方程x2＋2x−3＝0配方后，可变形为                                                （    ）A．（x＋2）2＝3      B．（x＋1）2＝4      C．（x＋1）2＝2      D．（x＋1）2＝﹣24．下列说法中，正确的是                                                              （    ）A．同弦所对的圆周角相等          B．三角形的外心到三个顶点的距离相等 C．长度相等的两条弧是等弧         D．任意三点确定一个圆5．如图，AB是⊙O的直径，弦CD⊥AB于点E，BE＝2，CD＝8，则⊙O半径为               （    ）A．2              B．3                 C．5               D．86．如图，在直角坐标系中，△OAB和△OCD是位似图形，O为位似中心，若A点的坐标为（1，1），B点的坐标为（2，1），C点的坐标为（3，3），那么点D的坐标是                            （    ） A．（4，2）     B．（6，3）          C．（8，4）            D．（8，3）7．如图，AB是⊙O的直径，点C，D，E在⊙O上，若∠C＝100°，则∠E的度数为           （    ）A．10°         B．20°             C．30°               D．40°        8．我国古代数学家赵爽（公元3～4世纪）在其所著的《勾股圆方图注》中记载过一元二次方程（正根）的几何解法．以方程x2＋2x﹣35＝0即x（x＋2）＝35为例说明，记载的方法是：构造如图，大正方形的面积是（x＋x＋2）2．同时它又等于四个矩形的面积加上中间小正方形的面积，即4×35＋22，因此x＝5．则在下面四个构图中，能正确说明方程x2−2x−8＝0解法的构图是                      （    ）     A．           B．             C．                D． 9．如图，在△ABC中，∠BAC＝45°，BD、CE分别是AC、AB边上的高，连接DE，若BC＝2，则DE的长为                                                                           （    ）A．          B．            C．                D．10．在平面直角坐标系xOy中，点A，B分别在x，y轴的正半轴上，始终保持AB＝6，以AB为边向右上方作正方形ABCD，AC，BD交于点P，连接OP．下列结论正确的个数是                  （    ）（1）直线OP的函数表达式为y＝x；（2）OP的取值范围是3< OP < 6 ；（3）若B点的坐标为(4−，0)时,则OP＝4；（4）连接OD，则OD的最大值为3＋3；（5）四边形AOBP面积的最大值为18．A．1个          B．2个              C．3个               D．4个       二、填空题（本大题共8小题，每题3分，共24分.其中第17题第一空1分，第二空2分．请把答案填写在答题卡上相应的位置）11．如图，要使△AFE∽△ABC，可以添加条件:      ▲         ．12. 已知△ABC与△A'B'C'是相似图形，相似比是1：3，则△ABC与△A'B'C'的周长比是   ▲      ．13．已知关于x的一元二次方程x2−8x＋c＝0有一个根为5，则c的值为     ▲      ．14．直角三角形的两直角边长分别为6和8，它的外接圆的半径是    ▲    ．15. 如图，树AB在路灯O的照射下形成投影AC，已知路灯高PO=5m，树影AC=3m，树AB与路灯O的地面距离AP=4.5m，则树的高度AB长是     ▲     m.16.“十一”假期，小明和同学一起到游乐场游玩，游乐场的大型摩天轮的半径为15m，旋转1周需要24min(匀速). 小明乘坐最底部(离地面约1m）的车厢按逆时针方向旋转开始1周的观光，启动10min时，小明离地面的高度是     ▲     m．已知：在平面直角坐标系xOy中,点A（0，3）、B（10，0），在x轴上存在一点P，使AP＋BP的值最小，此时P的坐标为      ▲     ，AP＋BP的最小值为      ▲      .如图，△ABC 中，CA=CB，D为BC延长线上一点，过点D作DE⊥AD，交AC延长线于E，若∠B＝2∠DAC，AE＝8,BD＝11，则AD=      ▲      .         三、解答题（本大题共10小题，共96分）19．（本题12分）用适当的方法解方程：（1）3x2−x＝0；          （2）x2−2x−5＝0；       （3）（x＋1）（2x−5）＝4；20.（本题8分）已知：＝，求下列各式的值（1） ；           （2）．21．（本题8分）如图，∠BAD＝∠CAE，∠B＝∠D．（1）△ABC和△ADE相似吗？为什么？（2）如果AB＝2AD，BC＝4，那么DE的长度为多少？    22．（本题7分）如图，某建筑工程队在一堵墙边上用24米长的铁栏围成一个面积为84平方米的长方形仓库，已知可利用的墙长是13米，铁栅栏只围三边，且在正下方要造一个2米宽的门．问：（1）设仓库垂直于墙的一边长为x米，则仓库平行于墙的一边长为      ▲       米；（2）以上要求所围成长方形的两条邻边的长分别是多少米？ 23．（本题8分）如图，在平面直角坐标系中，已知△ABC三个顶点的坐标分别是A（−2，2），B（0，4），C（4，4）．（1）以点O为位似中心，将△ABC缩小为原来的得到△A1B1C1，请在x轴下方画出△A1B1C1；点P（a，b）为△ABC内的一点，则点P在△A1B1C1内部的对应点P1的坐标为 　     ▲        　．（2）△ABC外接圆的圆心坐标为 　    ▲    　，外接圆的半径是 　     ▲         　．24．（本题10分）已知在△ABC中，BC＞AB，请用直尺（不带刻度）和圆规在AC上作出符合要求的一点P．（作图不必写作法，但要保留作图痕迹．）（1）如图1，若∠A＝90°，使得点P到BC的距离等于PA；（2）如图2，若∠A＜90°，使得点P到BC的距离等于PA；（3）在（2）的条件下，若∠A＝75°，∠C＝45°，AB＝6，则PA＝     ▲     ．        25．（本题11分）我们在探究一元二次方程根与系数的关系中发现：如果关于x的方程ax2＋bx＋c＝0的两个根是x1，x2，那么由求根公式可推出x1＋x2＝−，x1•x2＝，请根据这一结论，解决下列问题：（1）若α，β是方程2x2＋x−5＝0的两根，则α＋β＝     ▲       ，α•β＝    ▲        ； 若2，3是方程x2＋px＋q＝0的两根，则p＝    ▲   ，q＝    ▲   ；（2）已知m，n满足m2＋5m−3＝0，n2＋5n−3＝0，求＋的值；（3）已知a，b，c满足a＋b−2c＝0，abc＝9，则正整数c的最小值为    ▲      ． 26．（本题12分）如图，AB是⊙O的直径，弦CD⊥AB于点E，G是弧AC上一点，AG，DC的延长线交于点F，连接AD，GD，GC．（1）求证：∠ADG＝∠F；（2）已知AE＝CD，BE＝2．①求⊙O的半径长；②若点G是AF的中点，求DF的长．      27．（本题10分）【基本图形】（1）如图1，在矩形ABCD中，CE⊥BD于点H，交AD于点E．求证：＝； 【类比探究】（2）如图2，在四边形ABCD中，∠A＝∠B＝90°，AD＝4，BC＝9，CD＝7．E是边AB上的一动点，过点C作CG⊥ED，交ED的延长线于点G，交AD的延长线于点F．试探究是否为定值？若是，请求出的值；若不是，请说明理由；【拓展延伸】（3）如图3，在Rt△ABD中，∠BAD＝90°，将△ABD沿BD翻折得到△CBD，点E，F分别在边AB，AD上，连接CF，DE．若∠AED＝∠AFC，且＝，则  的值为　  ▲  　（直接写出结果）．        28．（本题10分）如图，△ABC中，BD为角平分线（1）如图1，请说明AB：BC=AD：CD；（2）如图2，若∠ABC＝90°，AB=2。请直接利用（1）的结论求出AD2+CD2的最小值．