




中考数学一轮复习核心考点精讲精练专题24 图形的变换(2份打包,原卷版+解析版)
展开专题24 图形的变换
一、轴对称变换
【核心考点精讲】
1、轴对称图形
把一个图形沿一条直线折叠,直线两边的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴,折叠后重合的对应点,叫做对称点。常见的轴对称图形:等腰三角形,矩形,正方形,等腰梯形,圆等。
2、轴对称性质
(1)关于直线对称的两个图形是全等图形。
(2)对称轴是对应点连线的垂直平分线。
(3)如果两个图形的对应点连线被同一直线垂直平分,那么这两个图形关于这条直线对称。
3、关于x轴、y轴对称的点的坐标
(1)关于x轴的对称点的坐标特点:横坐标不变,纵坐标互为相反数,即点P(x,y)关于x轴的对称点P′的坐标是(x,﹣y);
(2)关于y轴的对称点的坐标特点:横坐标互为相反数,纵坐标不变,即点P(x,y)关于y轴的对称点P′的坐标是(﹣x,y)。
4、最短路线问题
在直线l上方有两个点A、B,确定直线l上到A、B的距离之和最短的点,可以通过轴对称来确定,即作出其中一点关于直线l的对称点,对称点与另一点的连线与直线l的交点即为所求。
【热点题型精练】
1.(2022•天津中考)在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( )
A. B. C. D.
解:选项A、C、B不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形,
选项D能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形,
答案:D.
2.(2022•北京中考)图中的图形为轴对称图形,该图形的对称轴的条数为( )
A.1 B.2 C.3 D.5
解:如图所示,该图形有5条对称轴,
答案:D.
3.(2022•常州中考)在平面直角坐标系xOy中,点A与点A1关于x轴对称,点A与点A2关于y轴对称.已知点A1(1,2),则点A2的坐标是( )
A.(﹣2,1) B.(﹣2,﹣1) C.(﹣1,2) D.(﹣1,﹣2)
解:∵点A与点A1关于x轴对称,已知点A1(1,2),
∴点A的坐标为(1,﹣2),
∵点A与点A2关于y轴对称,
∴点A2的坐标为(﹣1,﹣2),
答案:D.
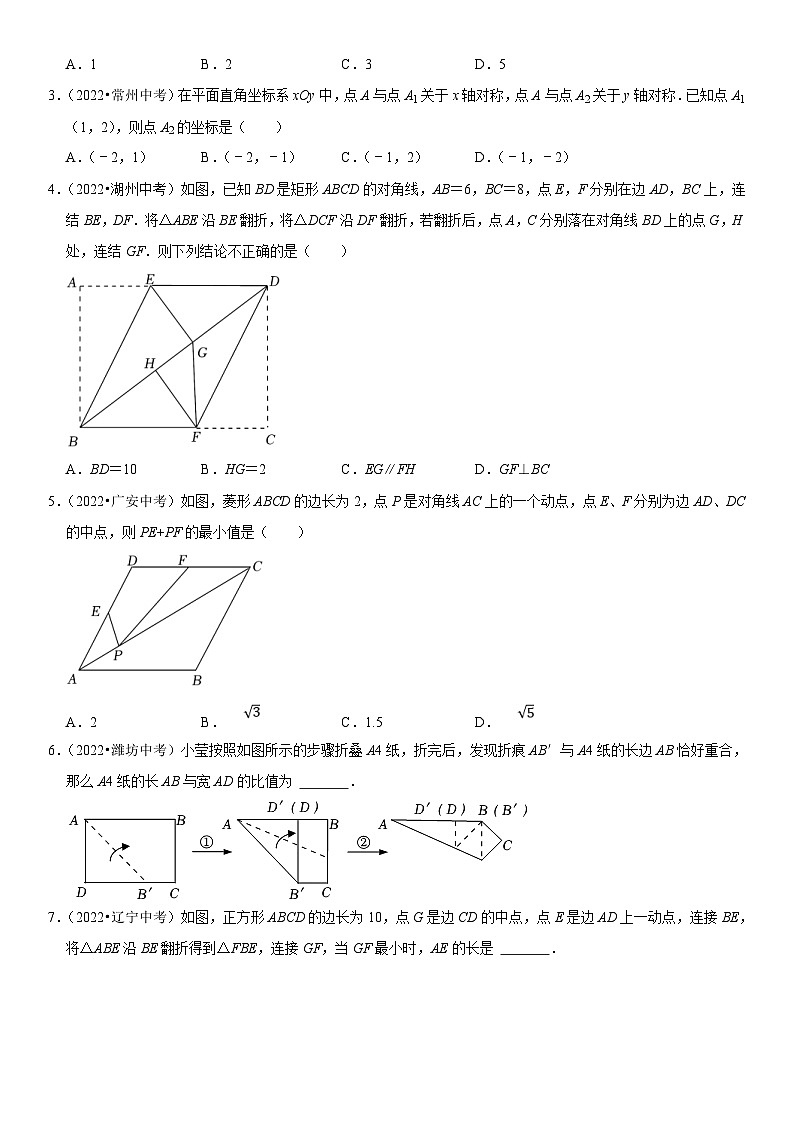
4.(2022•湖州中考)如图,已知BD是矩形ABCD的对角线,AB=6,BC=8,点E,F分别在边AD,BC上,连结BE,DF.将△ABE沿BE翻折,将△DCF沿DF翻折,若翻折后,点A,C分别落在对角线BD上的点G,H处,连结GF.则下列结论不正确的是( )
A.BD=10 B.HG=2 C.EG∥FH D.GF⊥BC
解:∵四边形ABCD是矩形,
∴∠A=90°,BC=AD,
∵AB=6,BC=8,
∴BD10,
故A选项不符合题意;
∵将△ABE沿BE翻折,将△DCF沿DF翻折,点A,C分别落在对角线BD上的点G,H处,
∴AB=BG=6,CD=DH=6,
∴GH=BG+DH﹣BD=6+6﹣10=2,
故B选项不符合题意;
∵四边形ABCD是矩形,
∴∠A=∠C=90°,
∵将△ABE沿BE翻折,将△DCF沿DF翻折,点A,C分别落在对角线BD上的点G,H处,
∴∠A=∠BGE=∠C=∠DHF=90°,
∴EG∥FH.
故C选项不符合题意;
∵GH=2,
∴BH=DG=BG﹣GH=6﹣2=4,
设FC=HF=x,则BF=8﹣x,
∴x2+42=(8﹣x)2,
∴x=3,
∴CF=3,
∴,
又∵,
∴,
若GF⊥BC,则GF∥CD,
∴,
故D选项符合题意.
答案:D.
5.(2022•广安中考)如图,菱形ABCD的边长为2,点P是对角线AC上的一个动点,点E、F分别为边AD、DC的中点,则PE+PF的最小值是( )
A.2 B. C.1.5 D.
解:如图,取AB的中点T,连接PT,FT.
∵四边形ABCD是菱形,
∴CD∥AB,CD=AB,
∵DF=CF,AT=TB,
∴DF=AT,DF∥AT,
∴四边形ADFT是平行四边形,
∴AD=FT=2,
∵四边形ABCD是菱形,AE=DE,AT=TB,
∴E,T关于AC对称,
∴PE=PT,
∴PE+PF=PT+PF,
∵PF+PT≥FT=2,
∴PE+PF≥2,
∴PE+PF的最小值为2.
答案:A.
6.(2022•潍坊中考)小莹按照如图所示的步骤折叠A4纸,折完后,发现折痕AB′与A4纸的长边AB恰好重合,那么A4纸的长AB与宽AD的比值为 .
解:由第②次折叠知,AB=AB',
由第①次折叠知,∠B'AB=45°,
∴△AD'B'是等腰直角三角形,
∴AB'AD',
∴AB与宽AD的比值为,
答案:,
7.(2022•辽宁中考)如图,正方形ABCD的边长为10,点G是边CD的中点,点E是边AD上一动点,连接BE,将△ABE沿BE翻折得到△FBE,连接GF,当GF最小时,AE的长是 55 .
解:∵将△ABE沿BE翻折得到△FBE,
∴BF=BA=10,
∴点F在以B为圆心,10为半径的圆上运动,
∴当点G、F、B三点共线时,GF最小,
连接EG,设AE=x,
由勾股定理得,BG=5,
∵S梯形ABGD=S△EDG+S△ABE+S△EBG,
∴(5+10)×10,
解得x=55,
∴AE=55,
答案:55.
8.(2022•镇江中考)如图,有一张平行四边形纸片ABCD,AB=5,AD=7,将这张纸片折叠,使得点B落在边AD上,点B的对应点为点B′,折痕为EF,若点E在边AB上,则DB′长的最小值等于 2 .
解:由折叠可知,BE=B'E,BF=B'F,如图,当E与A重合时,B'D最短.
∵AB=5,AD=7,
∴AB'=5,
∴B'D=AD﹣AB'=7﹣5=2,
即DB′长的最小值为2.
答案:2.
9.(2022•眉山中考)如图,点P为矩形ABCD的对角线AC上一动点,点E为BC的中点,连接PE,PB,若AB=4,BC=4,则PE+PB的最小值为 6 .
解:如图,作点B关于AC的对称点B',交AC于点F,连接B′E交AC于点P,则PE+PB的最小值为B′E的长度,
∵四边形ABCD为矩形,
∴AB=CD=4,∠ABC=90°,
在Rt△ABC中,AB=4,BC=4,
∴tan∠ACB,
∴∠ACB=30°,
由对称的性质可知,B'B=2BF,B'B⊥AC,
∴BFBC=2,∠CBF=60°,
∴B′B=2BF=4,
∵BE=BF,∠CBF=60°,
∴△BEF是等边三角形,
∴BE=BF=B'F,
∴△BEB'是直角三角形,
∴B′E6,
∴PE+PB的最小值为6,
答案:6.
10.(2022•鄂尔多斯中考)如图,在△ABC中,AB=AC=4,∠CAB=30°,AD⊥BC,垂足为D,P为线段AD上的一动点,连接PB、PC.则PA+2PB的最小值为 4 .
解:如图,
在∠BAC的外部作∠CAE=15°,作BF⊥AE于F,交AD于P,
此时PA+2PB最小,
∴∠AFB=90°
∵AB=AC,AD⊥BC,
∴∠CAD=∠BAD,
∴∠EAD=∠CAE+∠CAD=30°,
∴PF,
∴PA+2PB=2()=2(PF+PB)=2BF,
在Rt△ABF中,AB=4,∠BAF=∠BAC+∠CAE=45°,
∴BF=AB•sin45°=42,
∴(PA+2PB)最小=2BF=4,
答案:4.
11.(2022•连云港中考)如图,四边形ABCD为平行四边形,延长AD到点E,使DE=AD,且BE⊥DC.
(1)求证:四边形DBCE为菱形;
(2)若△DBC是边长为2的等边三角形,点P、M、N分别在线段BE、BC、CE上运动,求PM+PN的最小值.
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵DE=AD,
∴DE=BC,
∵E在AD的延长线上,
∴DE∥BC,
∴四边形DBCE是平行四边形,
∵BE⊥DC,
∴四边形DBCE是菱形;
(2)解:作N关于BE的对称点N',过D作DH⊥BC于H,如图:
由菱形的对称性知,点N关于BE的对称点N'在DE上,
∴PM+PN=PM+PN',
∴当P、M、N'共线时,PM+PN'=MN'=PM+PN,
∵DE∥BC,
∴MN'的最小值为平行线间的距离DH的长,即PM+PN的最小值为DH的长,
在Rt△DBH中,
∠DBC=60°,DB=2,
∴DH=DB•sin∠DBC=2,
∴PM+PN的最小值为.
12.(2022•枣庄中考)已知△ABC中,∠ACB=90°,AC=BC=4cm,点P从点A出发,沿AB方向以每秒cm的速度向终点B运动,同时动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,设运动的时间为t秒.
(1)如图①,若PQ⊥BC,求t的值;
(2)如图②,将△PQC沿BC翻折至△P′QC,当t为何值时,四边形QPCP′为菱形?
解:(1)如图①,∵∠ACB=90°,AC=BC=4cm,
∴AB4(cm),
由题意得,APtcm,BQ=tcm,
则BP=(4t)cm,
∵PQ⊥BC,
∴∠PQB=90°,
∴∠PQB=∠ACB,
∴PQ∥AC,
∴,
∴,
解得:t=2,
∴当t=2时,PQ⊥BC.
(2)作PD⊥BC于D,PE⊥AC于E,如图②,
APtcm,BQ=tcm(0≤t<4),
∵∠C=90°,AC=BC=4cm,
∴△ABC为等腰直角三角形,
∴∠A=∠B=45°,
∴△APE和△PBD为等腰直角三角形,
∴PE=AEAP=tcm,BD=PD,
∴CE=AC﹣AE=(4﹣t)cm,
∵四边形PECD为矩形,
∴PD=EC=(4﹣t)cm,
∴BD=(4﹣t)cm,
∴QD=BD﹣BQ=(4﹣2t)cm,
在Rt△PCE中,PC2=PE2+CE2=t2+(4﹣t)2,
在Rt△PDQ中,PQ2=PD2+DQ2=(4﹣t)2+(4﹣2t)2,
∵四边形QPCP′为菱形,
∴PQ=PC,
∴t2+(4﹣t)2=(4﹣t)2+(4﹣2t)2,
∴t1,t2=4(舍去).
∴当t的值为时,四边形QPCP′为菱形.
二、平移变换
【核心考点精讲】
1、把一个图形整体沿某一直线方向移动一定的距离,得到一个新的图形,图形的这种移动,叫做平移。
2、平移的两个要素:(1)图形平移的方向;(2)图形平移的距离。
3、平移性质:对应点所连线段平行且相等。
4、平移变换与坐标变化
(1)坐标点P(x,y)向右平移a个单位,得出P(x+a,y);
(2)坐标点P(x,y)向左平移a个单位,得出P(x﹣a,y);
(3)坐标点P(x,y)向上平移b个单位,得出P(x,y+b);
(4)坐标点P(x,y)向下平移b个单位,得出P(x,y﹣b)。
【热点题型精练】
13.(2022•广西中考)2022北京冬残奥会的会徽是以汉字“飞”为灵感来设计的,展现了运动员不断飞跃,超越自我,奋力拼搏,激励世界的冬残奥精神.下列的四个图中,能由如图所示的会徽经过平移得到的是( )
A. B. C. D.
解:根据平移的性质可知:能由如图经过平移得到的是D,
答案:D.
14.(2022•海南中考)如图,点A(0,3)、B(1,0),将线段AB平移得到线段DC,若∠ABC=90°,BC=2AB,则点D的坐标是( )
A.(7,2) B.(7,5) C.(5,6) D.(6,5)
解:过点D作DE⊥y轴于点E,如图,
∵点A(0,3)、B(1,0),
∴OA=3,OB=1.
∵线段AB平移得到线段DC,
∴AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
∵∠ABC=90°,
∴四边形ABCD是矩形.
∴∠BAD=90°,BC=AD.
∵BC=2AB,
∴AD=2AB.
∵∠BAO+∠DAE=90°,∠BAO+∠ABO=90°,
∴∠ABO=∠EAD.
∵∠AOB=∠AED=90°,
∴△ABO∽△DAE.
∴.
∴DE=2OA=6,AE=2OB=2,
∴OE=OA+AE=5,
∴D(6,5).
答案:D.
15.(2022•百色中考)如图,在△ABC中,点A(3,1),B(1,2),将△ABC向左平移2个单位,再向上平移1个单位,则点B的对应点B′的坐标为( )
A.(3,1) B.(3,3) C.(﹣1,1) D.(﹣1,3)
解:根据平移与图形变化的规律可知,
将△ABC向左平移2个单位,再向上平移1个单位,其图形上的对应点B′的横坐标减少2,纵坐标增加1,
由于点B(1,2),
所以平移后的对应点B′的坐标为(﹣1,3),
答案:D.
16.(2022•嘉兴中考)“方胜”是中国古代妇女的一种发饰,其图案由两个全等正方形相叠组成,寓意是同心吉祥.如图,将边长为2cm的正方形ABCD沿对角线BD方向平移1cm得到正方形A′B′C′D′,形成一个“方胜”图案,则点D,B′之间的距离为( )
A.1cm B.2cm C.(1)cm D.(21)cm
解:∵四边形ABCD为边长为2cm的正方形,
∴BD2(cm),
由平移的性质可知,BB′=1cm,
∴B′D=(21)cm,
答案:D.
17.(2022•福建中考)如图,现有一把直尺和一块三角尺,其中∠ABC=90°,∠CAB=60°,AB=8,点A对应直尺的刻度为12.将该三角尺沿着直尺边缘平移,使得△ABC移动到△A′B′C′,点A′对应直尺的刻度为0,则四边形ACC′A′的面积是( )
A.96 B.96 C.192 D.160
解:在Rt△ABC中,∠CAB=60°,AB=8,
则BC=AB•tan∠CAB=8,
由平移的性质可知:AC=A′C′,AC∥A′C′,
∴四边形ACC′A′为平行四边形,
∵点A对应直尺的刻度为12,点A′对应直尺的刻度为0,
∴AA′=12,
∴S四边形ACC′A′=12×896,
答案:B.
18.(2022•淄博中考)如图,在平面直角坐标系中,平移△ABC至△A1B1C1的位置.若顶点A(﹣3,4)的对应点是A1(2,5),则点B(﹣4,2)的对应点B1的坐标是 (1,3) .
解:∵点A(﹣3,4)的对应点是A1(2,5),
∴点B(﹣4,2)的对应点B1的坐标是(1,3).
答案:(1,3).
19.(2022•大连中考)如图,在平面直角坐标系中,点A的坐标是(1,2),将线段OA向右平移4个单位长度,得到线段BC,点A的对应点C的坐标是 (5,2) .
解:将线段OA向右平移4个单位长度,得到线段BC,点A的对应点C的坐标是(1+4,2),即(5,2),
答案:(5,2).
20.(2022•临沂中考)如图,在平面直角坐标系中,△ABC的顶点A,B的坐标分别是A(0,2),B(2,﹣1).平移△ABC得到△A'B'C',若点A的对应点A'的坐标为(﹣1,0),则点B的对应点B'的坐标是 (1,﹣3) .
解:由题意知,点A从(0,2)平移至(﹣1,0),可看作是△ABC先向下平移2个单位,再向左平移1个单位(或者先向左平移1个单位,再向下平移2个单位),
即B点(2,﹣1),平移后的对应点为B'(1,﹣3),
答案:(1,﹣3).
21.(2022•毕节中考)如图,在平面直角坐标系中,把一个点从原点开始向上平移1个单位,再向右平移1个单位,得到点A1(1,1);把点A1向上平移2个单位,再向左平移2个单位,得到点A2(﹣1,3);把点A2向下平移3个单位,再向左平移3个单位,得到点A3(﹣4,0);把点A3向下平移4个单位,再向右平移4个单位,得到点A4(0,﹣4),…;按此做法进行下去,则点A10的坐标为 (﹣1,11) .
解:由图象可知,A5(5,1),
将点A5向左平移6个单位、再向上平移6个单位,可得A6(﹣1,7),
将点A6向左平移7个单位,再向下平移7个单位,可得A7(﹣8,0),
将点A7向右平移8个单位,再向下平移8个单位,可得A8(0,﹣8),
将点A8向右平移9个单位,再向上平移9个单位,可得A9(9,1),
将点A9向左平移10个单位,再向上平移10个单位,可得A10(﹣1,11),
答案:(﹣1,11).
22.(2022•陕西中考)如图,△ABC的顶点坐标分别为A(﹣2,3),B(﹣3,0),C(﹣1,﹣1).将△ABC平移后得到△A'B'C',且点A的对应点是A'(2,3),点B、C的对应点分别是B'、C'.
(1)点A、A'之间的距离是 4 ;
(2)请在图中画出△A'B'C'.
解:(1)∵A(﹣2,3),A'(2,3),
∴点A、A'之间的距离是2﹣(﹣2)=4,
答案:4;
(2)如图所示,△A'B'C'即为所求.
三、旋转变换
【核心考点精讲】
1、将一个图形绕一个定点沿某个方向转动一定的角度,这样的图形变换叫做旋转,这个定点叫做旋转中心,转动的角度叫做旋转角。
2、旋转性质
(1)对应点到旋转中心的距离相等.
(2)对应点与旋转中心所连线段的夹角等于旋转角。
(3)旋转前后的图形全等。
2、旋转作图
根据对应角相等且等于旋转角,对应线段相等,由此可以通过作相等的角,在角的边上截取相等线段的方法,找到对应点,顺次连接得出旋转后的图形。
【热点题型精练】
23.(2022•枣庄中考)剪纸文化是中国最古老的民间艺术之一,下列剪纸图案中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
解:A.不是中心对称图形,是轴对称图形,故此选项不合题意;
B.不是中心对称图形,是轴对称图形,故此选项不合题意;
C.是中心对称图形,不是轴对称图形,故此选项不合题意;
D.既是轴对称图形又是中心对称图形,故此选项符合题意;
答案:D.
24.(2022•青岛中考)如图,将△ABC先向右平移3个单位,再绕原点O旋转180°,得到△A'B'C',则点A的对应点A'的坐标是( )
A.(2,0) B.(﹣2,﹣3) C.(﹣1,﹣3) D.(﹣3,﹣1)
解:由图中可知,点A(﹣2,3),将△ABC先向右平移3个单位,得坐标为:(1,3),再绕原点O旋转180°,得到△A'B'C',则点A的对应点A'的坐标是(﹣1,﹣3).
答案:C.
25.(2022•天津中考)如图,在△ABC中,AB=AC,若M是BC边上任意一点,将△ABM绕点A逆时针旋转得到△ACN,点M的对应点为点N,连接MN,则下列结论一定正确的是( )
A.AB=AN B.AB∥NC C.∠AMN=∠ACN D.MN⊥AC
解:A、∵AB=AC,
∴AB>AM,
由旋转的性质可知,AN=AM,
∴AB>AN,故本选项结论错误,不符合题意;
B、当△ABC为等边三角形时,AB∥NC,除此之外,AB与NC不平行,故本选项结论错误,不符合题意;
C、由旋转的性质可知,∠BAC=∠MAN,∠ABC=∠ACN,
∵AM=AN,AB=AC,
∴∠ABC=∠AMN,
∴∠AMN=∠ACN,本选项结论正确,符合题意;
D、只有当点M为BC的中点时,∠BAM=∠CAM=∠CAN,才有MN⊥AC,故本选项结论错误,不符合题意;
答案:C.
26.(2022•包头中考)如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2,将△ABC绕点C顺时针旋转得到△A'B'C,其中点A'与点A是对应点,点B'与点B是对应点.若点B'恰好落在AB边上,则点A到直线A'C的距离等于( )
A.3 B.2 C.3 D.2
解:连接AA′,如图,
∵∠ACB=90°,∠BAC=30°,BC=2,
∴ACBC=2,∠B=60°,
∵将△ABC绕点C顺时针旋转得到△A'B'C,
∴CA=CA′,CB=CB′,∠ACA′=∠BCB′,
∵CB=CB′,∠B=60°,
∴△CBB′为等边三角形,
∴∠BCB′=60°,
∴∠ACA′=60°,
∴△CAA′为等边三角形,
过点A作AD⊥A'C于点D,
∴CDAC,
∴ADCD3,
∴点A到直线A'C的距离为3,
答案:C.
27.(2022•内蒙古中考)如图,边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,图中阴影部分的面积为( )
A. B. C.1 D.1
解:如图,设B′C′与CD的交点为E,连接AE,
在Rt△AB′E和Rt△ADE中,,
∴Rt△AB′E≌Rt△ADE(HL),
∴∠DAE=∠B′AE,
∵旋转角为30°,
∴∠DAB′=60°,
∴∠DAE60°=30°,
∴DE=1,
∴阴影部分的面积=1×1﹣2×(1)=1.
答案:C.
28.(2022•阜新中考)如图,在△ABC中,∠B=90°,AB=BC=4,将△ABC绕点A逆时针旋转60°,得到△ADE,则点D到BC的距离是 2 .
解:如图,连接BD,过点D作DH⊥BC于H,
∵将△ABC绕点A逆时针旋转60°,
∴AB=AD=4,∠BAD=60°,
∴△ABD是等边三角形,
∴BD=AB=4,∠ABD=60°,
∴∠DBC=30°,
∵DH⊥BC,
∴DHBD=2,
∴点D到BC的距离是2,
答案:2.
29.(2022•盘锦中考)如图,在△ABC中,AB=AC,∠ABC=30°,点D为BC的中点,将△ABC绕点D逆时针旋转得到△A'B'C',当点A的对应点A'落在边AB上时,点C'在BA的延长线上,连接BB',若AA'=1,则△BB'D的面积是 .
解:如图所示,设A'B'与BD交于点O,连接A'D和AD,
∵点D为BC的中点,AB=AC,∠ABC=30°,
∴AD⊥BC,A'D⊥B'C',A'D是∠B′A′C′的角平分线,AD是∠BAC的角平分线,
∴∠B'A'C'=120°,∠BAC=120°,
∴∠BAD=∠B'A'D=60°,
∵A'D=AD,
∴△A'AD是等边三角形,
∴A'A=AD=A'D=1,
∵∠BA'B'=180°﹣∠B'A'C'=60°,
∴∠BA'B'=∠A'AD,
∴A'B'∥AD,
∴A′O⊥BC,
∴,
∴,
∵A'B'=2A'D=2,
∵∠A'BD=∠A'DO=30°,
∴BO=OD,
∴,,
∴.
30.(2022•黄石中考)如图,等边△ABC中,AB=10,点E为高AD上的一动点,以BE为边作等边△BEF,连接DF,CF,则∠BCF= 30° ,FB+FD的最小值为 5 .
解:如图,
∵△ABC是等边三角形,AD⊥CB,
∴∠BAE∠BAC=30°,
∵△BEF是等边三角形,
∴∠EBF=∠ABC=60°,BE=BF,
∴∠ABE=∠CBF,
在△BAE和△BCF中,
,
∴△BAE≌△BCF(SAS),
∴∠BAE=∠BCF=30°,
作点D关于CF的对称点G,连接CG,DG,BG,BG交CF的延长线于点F′,连接DF′,此时BF′+DF′的值最小,最小值=线段BG的长.
∵∠DCF=∠FCG=30°,
∴∠DCG=60°,
∵CD=CG=5,
∴△CDG是等边三角形,
∴DB=DC=DG,
∴∠CGB=90°,
∴BG5,
∴BF+DF的最小值为5,
答案:30°,5.
31.(2022•广州中考)如图,在矩形ABCD中,BC=2AB,点P为边AD上的一个动点,线段BP绕点B顺时针旋转60°得到线段BP′,连接PP′,CP′.当点P′落在边BC上时,∠PP′C的度数为 120° ;当线段CP′的长度最小时,∠PP′C的度数为 75° .
解:如图,以AB为边向右作等边△ABE,连接EP′.
∵△BPP′是等边三角形,
∴∠ABE=∠PBP′=60°,BP=BP′,BA=BE,
∴∠ABP=∠EBP′,
在△ABP和△EBP′中,
,
∴△ABP≌△EBP′(SAS),
∴∠BAP=∠BEP′=90°,
∴点P′在射线EP′上运动,
如图1中,设EP′交BC于点O,
当点P′落在BC上时,点P′与O重合,此时∠PP′C=180°﹣60°=120°,
当CP′⊥EP′时,CP′的长最小,此时∠EBO=∠OCP′=30°,
∴EOOB,OP′OC,
∴EP′=EO+OP′OBOCBC,
∵BC=2AB,
∴EP′=AB=EB,
∴∠EBP′=∠EP′B=45°,
∴∠BP′C=45°+90°=135°,
∴∠PP′C=∠BP′C﹣∠BP′P=135°﹣60°=75°.
答案:120°,75°.
32.(2022•柳州中考)如图,在正方形ABCD中,AB=4,G是BC的中点,点E是正方形内一个动点,且EG=2,连接DE,将线段DE绕点D逆时针旋转90°得到线段DF,连接CF,则线段CF长的最小值为 22 .
解:连接DG,将DG绕点D逆时针旋转90°得DM,连接MG,CM,MF,
作MH⊥CD于H,
∵∠EDF=∠GDM,
∴∠EDG=∠FDM,
∵DE=DF,DG=DM,
∴△EDG≌△MDF(SAS),
∴MF=EG=2,
∵∠GDC=∠DMH,∠DCG=∠DHM,DG=DM,
∴△DGC≌△MDH(AAS),
∴CG=DH=2,MH=CD=4,
∴CM2,
∵CF≥CM﹣MF,
∴CF的最小值为22,
答案:22.
33.(2022•锦州中考)如图,在△ABC中,,D,E,F分别为AC,AB,BC的中点,连接DE,DF.
(1)如图1,求证:;
(2)如图2,将∠EDF绕点D顺时针旋转一定角度,得到∠PDQ,当射线DP交AB于点G,射线DQ交BC于点N时,连接FE并延长交射线DP于点M,判断FN与EM的数量关系,并说明理由;
(3)如图3,在(2)的条件下,当DP⊥AB时,求DN的长.
(1)证明:如图1,连接AF,
∵,D,E,F分别为AC,AB,BC的中点,
∴,AF⊥BC,
∴,
∴;
(2)解:,
理由如下:
连接AF,如图2,
∵,D,E,F分别为AC,AB,BC的中点,
∴,
∴四边形CDEF是平行四边形,
∴∠DEF=∠C,
∵,
∴∠DFC=∠C,
∴∠DFC=∠DEF,
∴180°﹣∠DFC=180°﹣∠DEF,
∴∠DFN=∠DEM,
∵将∠EDF绕点D顺时针旋转一定角度,得到∠PDQ,
∴∠EDF=∠PDQ,
∵∠FDN+∠NDE=∠EDM+∠NDE,
∴∠FDN=∠EDM,
∴△DNF∽△DME,
∴,
∴;
(3)解:如图,连接AF,过点C作CH⊥AB于H,
Rt△AFC中,,
∴,
∵,
∴,
∵DP⊥AB,
∴△AGD∽△AHC,
∴,
∴,
Rt△GED中,,
Rt△AGD中,,
∴,
∵EF∥AD,
∴∠EMG=∠ADG,
∴,
∴,
∴,
∵△DNF∽△DME,
∴,
∴.
34.(2022•连云港中考)【问题情境】
在一次数学兴趣小组活动中,小昕同学将一大一小两个三角板按照如图1所示的方式摆放.其中∠ACB=∠DEB=90°,∠B=30°,BE=AC=3.
【问题探究】
小昕同学将三角板DEB绕点B按顺时针方向旋转.
(1)如图2,当点E落在边AB上时,延长DE交BC于点F,求BF的长.
(2)若点C、E、D在同一条直线上,求点D到直线BC的距离.
(3)连接DC,取DC的中点G,三角板DEB由初始位置(图1),旋转到点C、B、D首次在同一条直线上(如图3),求点G所经过的路径长.
(4)如图4,G为DC的中点,则在旋转过程中,点G到直线AB的距离的最大值是 .
解:(1)由题意得,∠BEF=∠BED=90°,
在Rt△BEF中,∠ABC=30°,BE=3,
∴BF2;
(2)①当点E在BC上方时,
如图1,过点D作DH⊥BC于H,
在Rt△ABC中,AC=3,
∴tan∠ABC,
∴BC3,
在Rt△BED中,∠EBD=∠ABC=30°,BE=3,
∴DE=BE•tan∠DBE,
∵S△BCDCD•BEBC•DH,
∴DH1,
②当点E在BC下方时,如图2,
在Rt△BCE中,BE=3,BC=3,
根据勾股定理得,CE3,
∴CD=CE﹣DE=3,
过点D作DM⊥BC于M,
∵S△BDCBC•DMCD•BE,
∴DM1,
即点D到直线BC的距离为±1;
(3)如图3﹣1,连接CD,取CD的中点G,
取BC的中点O,连接GO,则OG∥AB,
∴∠COG=∠B=30°,
∴∠BOG=150°,
∵点G为CD的中点,点O为BC的中点,
∴GOBD,
∴点G是以点O为圆心,为半径的圆上,如图3﹣2,
∴三角板DEB由初始位置(图1),旋转到点C、B、D首次在同一条直线上时,点G所经过的轨迹为150°所对的圆弧,
∴点G所经过的路径长为π;
(4)如图4,过点O作OK⊥AB于K,
∵点O为BC的中点,BC=3,
∴OB,
∴OK=OB•sin30°,
由(3)知,点G是以点O为圆心,为半径的圆上,
∴点G到直线AB的距离的最大值是,
答案:.
中考数学一轮复习核心考点精讲精练专题22 尺规作图(2份打包,原卷版+解析版): 这是一份中考数学一轮复习核心考点精讲精练专题22 尺规作图(2份打包,原卷版+解析版),文件包含中考数学一轮复习核心考点精讲精练专题22尺规作图原卷版doc、中考数学一轮复习核心考点精讲精练专题22尺规作图解析版doc等2份试卷配套教学资源,其中试卷共29页, 欢迎下载使用。
中考数学一轮复习核心考点精讲精练专题21 圆(2份打包,原卷版+解析版): 这是一份中考数学一轮复习核心考点精讲精练专题21 圆(2份打包,原卷版+解析版),文件包含中考数学一轮复习核心考点精讲精练专题21圆原卷版doc、中考数学一轮复习核心考点精讲精练专题21圆解析版doc等2份试卷配套教学资源,其中试卷共62页, 欢迎下载使用。
中考数学一轮复习核心考点精讲精练专题11 分式方程(2份打包,原卷版+解析版): 这是一份中考数学一轮复习核心考点精讲精练专题11 分式方程(2份打包,原卷版+解析版),文件包含中考数学一轮复习核心考点精讲精练专题11分式方程原卷版doc、中考数学一轮复习核心考点精讲精练专题11分式方程解析版doc等2份试卷配套教学资源,其中试卷共18页, 欢迎下载使用。












