数学高考第一轮复习特训卷（文科）仿真模拟冲刺卷(一)

这是一份数学高考第一轮复习特训卷（文科）仿真模拟冲刺卷(一)，共6页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
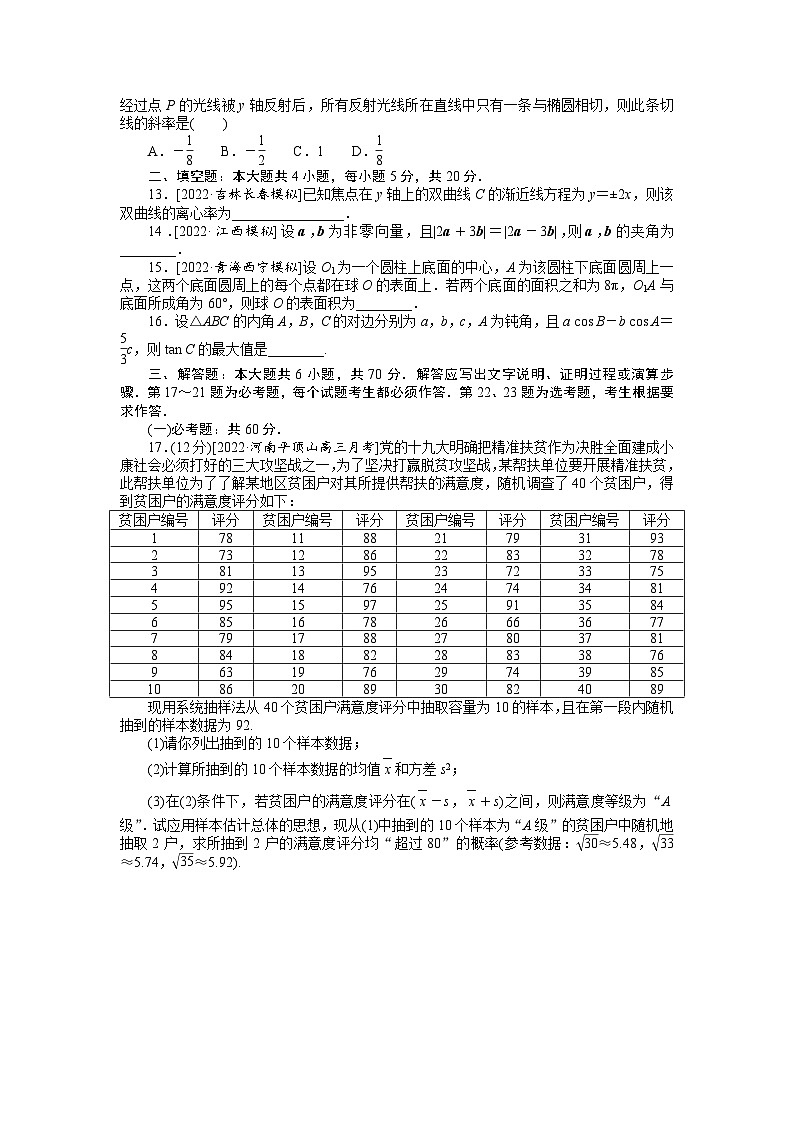
   　仿真模拟冲刺卷　　　　仿真模拟冲刺卷(一)时间：120分钟　满分：150分一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．[2022·山西太原一模]已知复数z满足＝i，则复数z＝(　　)A．1－i    B．1＋i    C．－1－i    D．－1＋i2．[2022·吉林东北师大附中高三月考]已知集合A＝，集合B＝，则A∩B＝(　　)A．[1，＋∞)    B．(1，＋∞)    C．(0，＋∞)    D．[0，＋∞)3．[2022·四川高三月考]已知命题p：∀x∈R，2sin x＋cos x≤；命题q：a>b>0且c<0，>.现有下列四个命题：①p∨q；②¬p∧q；③¬p∧¬q；④p∧¬q.其中真命题是(　　)A．①②    B．①④    C．②③    D．③④4．[2022·宁夏固原一中高三模拟]函数y＝x(ex－e－x)的图象大致为(　　)　　           5．[2022·云南昆明一中高三月考]已知实数x，y满足则z ＝2x－y的最小值是(　　)A．5    B．    C．0    D．－16．[2022·河南高三月考]已知函数f(x)＝为奇函数，则g(x)在x＝－1处的切线方程为(　　)A．x－y＝0    B．2x－y＋1＝0    C．x－2y＋1＝0    D．3x－y＋2＝07．[2022·四川成都模拟]已知Ω＝{(x，y)|x2＋y2<1}，在Ω中任取一点P(x，y)，则事件“xy<0”发生的概率为(　　)A．    B．    C．    D． 8．[2022·四川泸州模拟]如图，直四棱柱ABCD－A1B1C1D1的底面是正方形，已知AA1＝4，AB＝2，点E，F分别在棱BB1，CC1上，且BE＝BB1，CF＝CC1，则(　　)A.D1E≠AF，且直线D1E，AF是相交直线    B．D1E≠AF，且直线D1E，AF是异面直线C．D1E＝AF，且直线D1E，AF是异面直线    D.D1E＝AF，且直线D1E，AF是相交直线9．函数f(x)＝2sin (ωx＋φ)(ω>0，0<φ<π)的部分图象如图所示，要得到y＝f(x)的图象，只需将y＝2cos ωx的图象(　　)A．向右平移个单位长度    B．向右平移个单位长度C．向左平移个单位长度    D．向左平移个单位长度 10．某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度：在C处(点C在水平地面下方，O为CH与水平地面ABO的交点)进行该仪器的垂直弹射，水平地面上两个观察点A，B两地相距100米，∠BAC＝60°，其中A到C的距离比B到C的距离远40米．A地测得该仪器在C处的俯角为∠OAC＝15°，A地测得最高点H的仰角为∠HAO＝30°，则该仪器的垂直弹射高度CH为(　　)米A．210(＋)    B．140    C．210    D．20(－)11．[2022·河南驻马店高三月考]已知a＝log23，函数f(x)＝ex＋ln x－4的零点为b，g(x)＝x3－x2－x的极小值点为c，则(　　)A．b>a>c    B．a>b>c    C．c>b>a    D．b>c>a12．[2022·甘肃兰州一模]已知P(2，－2)是离心率为的椭圆＋＝1(a>b>0)外一点，经过点P的光线被y轴反射后，所有反射光线所在直线中只有一条与椭圆相切，则此条切线的斜率是(　　)A．－    B．－    C．1    D．二、填空题：本大题共4小题，每小题5分，共20分．13．[2022·吉林长春模拟]已知焦点在y轴上的双曲线C的渐近线方程为y＝±2x，则该双曲线的离心率为________________．14．[2022·江西模拟]设a，b为非零向量，且|2a＋3b|＝|2a－3b|，则a，b的夹角为________．15．[2022·青海西宁模拟]设O1为一个圆柱上底面的中心，A为该圆柱下底面圆周上一点，这两个底面圆周上的每个点都在球O的表面上．若两个底面的面积之和为8π，O1A与底面所成角为60°，则球O的表面积为________．16．设△ABC的内角A，B，C的对边分别为a，b，c，A为钝角，且a cos B－b cos A＝c，则tan C的最大值是________.三、解答题：本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．第17～21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．(一)必考题：共60分．17．(12分)[2022·河南平顶山高三月考]党的十九大明确把精准扶贫作为决胜全面建成小康社会必须打好的三大攻坚战之一，为了坚决打赢脱贫攻坚战，某帮扶单位要开展精准扶贫，此帮扶单位为了了解某地区贫困户对其所提供帮扶的满意度，随机调查了40个贫困户，得到贫困户的满意度评分如下：贫困户编号评分贫困户编号评分贫困户编号评分贫困户编号评分1781188217931932731286228332783811395237233754921476247434815951597259135846851678266636777791788278037818841882288338769631976297439851086208930824089现用系统抽样法从40个贫困户满意度评分中抽取容量为10的样本，且在第一段内随机抽到的样本数据为92.(1)请你列出抽到的10个样本数据；(2)计算所抽到的10个样本数据的均值和方差s2；(3)在(2)条件下，若贫困户的满意度评分在(－s，＋s)之间，则满意度等级为“A级”．试应用样本估计总体的思想，现从(1)中抽到的10个样本为“A级”的贫困户中随机地抽取2户，求所抽到2户的满意度评分均“超过80”的概率(参考数据：≈5.48，≈5.74，≈5.92).             18．(12分)[2021·四川郫都高三月考]已知Sn是等差数列{an}的前n项和，a2＝1.从下面的两个条件中任选其中一个：①2a5－a3＝11；②S4＝8，求解下列问题：(1)求数列{an}的通项；(2)设bn＝，试比较数列{bn}的前n项和Tn与的大小．注：条件①、②只能任选其一，若两个都选，则以条件①计分．            19.(12分)如图，在直三棱柱A′B′C′­ABC中，AD＝A′D，E为BC′上的一点，AB＝AC＝BC＝a，CC′＝h.(1)若BE＝EC′，求证：DE⊥平面BCC′B′.(2)平面BC′D将棱柱A′B′C′­ABC分割为两个几何体，记上面一个几何体的体积为V1，下面一个几何体的体积为V2，求的值．      20．(12分)[2022·山西长治高三月考]已知抛物线C：y2＝2px(p>0)的焦点为F，且点F与圆M：(x＋4)2＋y2＝1上点的距离的最小值为4.(1)求C的方程；(2)设点T(1，1)，过点T且斜率存在的两条直线分别交曲线C于A，B两点和P，Q两点，且|TA|·|TB|＝|TP|·|TQ|，求直线AB的斜率与直线PQ的斜率之和．                              21．(12分)[2022·安徽合肥模拟]已知函数f(x)＝(x＋1)ln x，曲线y＝f(x)在x＝1处的切线方程为y＝g(x).(1)求证：当x>1时，f(x)>g(x)；(2)求证：＋＋…＋>－(n≥2，n∈N*).        (二)选考题：共10分．请考生在第22、23题中任选一题作答．如果多做，则按所做的第一题计分．22．[选修4－4：坐标系与参数方程](10分)[2021·青海西宁三模]在平面直角坐标系xOy中，曲线C1的参数方程为(θ为参数)，曲线C2的参数方程为(φ为参数).(1)将C1，C2的方程化为普通方程，并说明它们分别表示什么曲线？(2)以坐标原点为极点，以x轴的正半轴为极轴，建立极坐标系，已知直线l的极坐标方程为ρ(cos θ－2sin θ)＝4.若C1上的点P对应的参数为θ＝，点Q在C2上，点M为PQ的中点，求点M到直线l距离的最小值．       23．[选修4－5：不等式选讲](10分)[2022·甘肃省民乐县第一中学模拟]已知f(x)＝2|x－2|＋|x＋a|.(1)当a＝2时，求不等式f(x)>5的解集；(2)设不等式f(x)≤|2x＋1|的解集为B，若[3，6]⊆B，求a的取值范围．