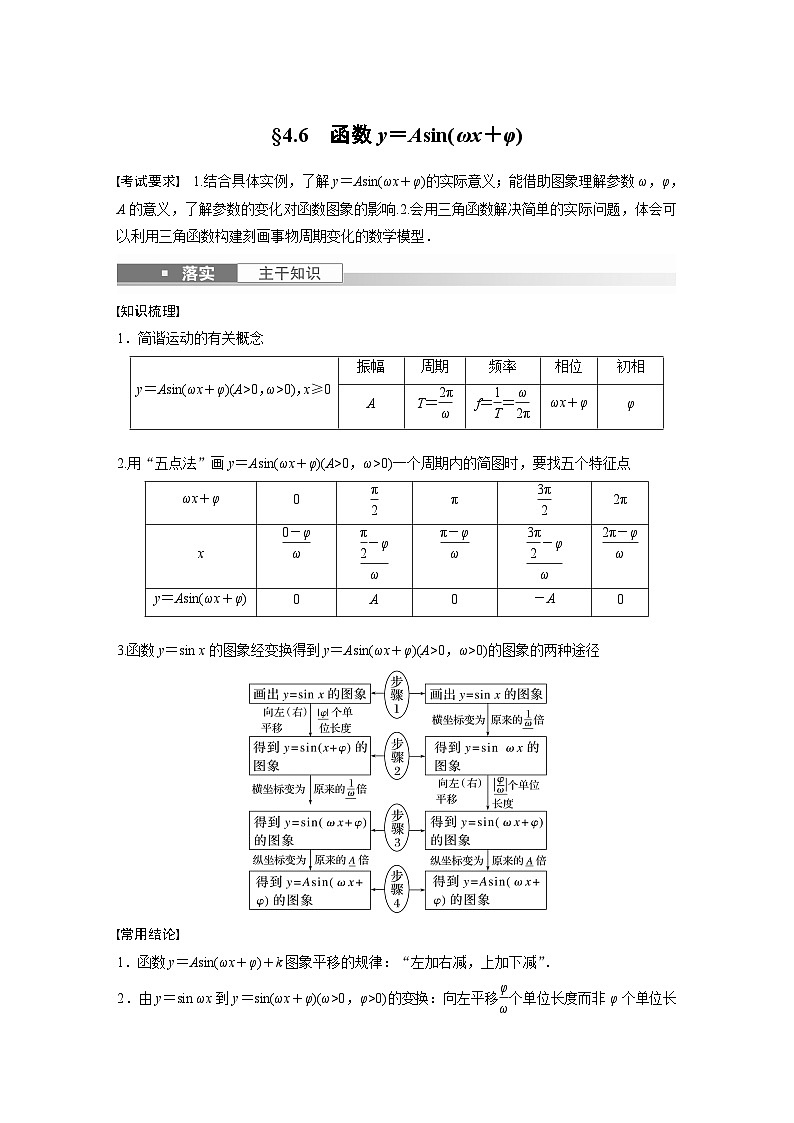
高考数学第一轮复习第四章 §4.6　函数y＝Asin(ωx＋φ)

这是一份高考数学第一轮复习第四章 §4.6　函数y＝Asin(ωx＋φ)，共29页。


知识梳理
1．简谐运动的有关概念
2.用“五点法”画y＝Asin(ωx＋φ)(A>0，ω>0)一个周期内的简图时，要找五个特征点
3.函数y＝sin x的图象经变换得到y＝Asin(ωx＋φ)(A>0，ω>0)的图象的两种途径
常用结论
1．函数y＝Asin(ωx＋φ)＋k图象平移的规律：“左加右减，上加下减”．
2．由y＝sin ωx到y＝sin(ωx＋φ)(ω>0，φ>0)的变换：向左平移eq \f(φ,ω)个单位长度而非φ个单位长度．
3．函数y＝Asin(ωx＋φ)图象的对称轴由ωx＋φ＝kπ＋eq \f(π,2)，k∈Z确定；对称中心由ωx＋φ＝kπ，k∈Z确定其横坐标．
思考辨析
判断下列结论是否正确(请在括号中打“√”或“×”)
(1)把y＝sin x的图象上各点的横坐标缩短为原来的eq \f(1,2)，纵坐标不变，所得图象对应的函数解析式为y＝sin eq \f(1,2)x.( × )
(2)将y＝sin 2x的图象向右平移eq \f(π,6)个单位长度，得到y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,3)))的图象．( √ )
(3)函数f(x)＝Asin(ωx＋φ)(A≠0)的最大值为A，最小值为－A.( × )
(4)如果y＝Acs(ωx＋φ)的最小正周期为T，那么函数图象的相邻两个对称中心之间的距离为eq \f(T,2).( √ )
教材改编题
1．为了得到函数y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(3x－\f(π,4)))的图象，只要把y＝sin 3x的图象( )
A．向右平移eq \f(π,4)个单位长度
B．向左平移eq \f(π,4)个单位长度
C．向右平移eq \f(π,12)个单位长度
D．向左平移eq \f(π,12)个单位长度
答案 C
2．为了得到y＝3cseq \b\lc\(\rc\)(\a\vs4\al\c1(3x＋\f(π,8)))的图象，只需把y＝3cseq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,8)))图象上的所有点的( )
A．纵坐标伸长到原来的3倍，横坐标不变
B．横坐标伸长到原来的3倍，纵坐标不变
C．纵坐标缩短到原来的eq \f(1,3)，横坐标不变
D．横坐标缩短到原来的eq \f(1,3)，纵坐标不变
答案 D
3．如图，某地一天从6～14时的温度变化曲线近似满足函数y＝Asin(ωx＋φ)＋b，A>0,0<φ<π，则这段曲线的函数解析式为__________________________．
答案 y＝10sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,8)x＋\f(3π,4)))＋20，x∈[6,14]
解析 从题图中可以看出，从6～14时的图象是函数y＝Asin(ωx＋φ)＋b的半个周期，
所以A＝eq \f(1,2)×(30－10)＝10，
b＝eq \f(1,2)×(30＋10)＝20，
又eq \f(1,2)×eq \f(2π,ω)＝14－6，所以ω＝eq \f(π,8).
又eq \f(π,8)×10＋φ＝2kπ，k∈Z,0<φ<π，
所以φ＝eq \f(3π,4)，
所以y＝10sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,8)x＋\f(3π,4)))＋20，x∈[6,14]．
题型一 函数y＝Asin(ωx＋φ)的图象及变换
例1 (1)(2021·全国乙卷)把函数y＝f(x)图象上所有点的横坐标缩短到原来的eq \f(1,2)倍，纵坐标不变，再把所得曲线向右平移eq \f(π,3)个单位长度，得到函数y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,4)))的图象，则f(x)等于( )
A．sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(x,2)－\f(7π,12))) B．sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(x,2)＋\f(π,12)))
C．sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(7π,12))) D．sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,12)))
答案 B
解析 依题意，将y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,4)))的图象向左平移eq \f(π,3)个单位长度，再将所得曲线上所有点的横坐标扩大到原来的2倍，得到f(x)的图象，
所以y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,4)))
eq \(―――――――――――――→,\s\up11(将其图象向左平移\f(π,3)个单位长度))y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,12)))的图象eq \(――――――――――――――→,\s\up7(所有点的横坐标扩大到原来的2倍))
f(x)＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(x,2)＋\f(π,12)))的图象．
(2)(2022·天津二中模拟)将函数y＝sin 2x的图象向左平移φeq \b\lc\(\rc\)(\a\vs4\al\c1(0≤φ<\f(π,2)))个单位长度后，得到函数y＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,6)))的图象，则φ等于( )
A.eq \f(π,12) B.eq \f(π,6)
C.eq \f(π,3) D.eq \f(5π,3)
答案 C
解析 y＝sin 2x＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,2))).
将函数y＝sin 2x的图象向左平移φ个单位长度后，
得到函数y＝cseq \b\lc\[\rc\](\a\vs4\al\c1(2x＋φ－\f(π,2)))
＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋2φ－\f(π,2)))
＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,6)))，
由题意知2φ－eq \f(π,2)＝eq \f(π,6)＋2kπ(k∈Z)，
则φ＝eq \f(π,3)＋kπ(k∈Z)，
又0≤φ教师备选
1．要得到函数y＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,6)))的图象，可以把函数y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,6)))的图象( )
A．向右平移eq \f(π,6)个单位长度
B．向右平移eq \f(π,12)个单位长度
C．向左平移eq \f(π,6)个单位长度
D．向左平移eq \f(π,12)个单位长度
答案 D
解析 函数y＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,6)))
＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,6)＋\f(π,2)))
＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,6)＋\f(π,6)))
＝sineq \b\lc\[\rc\](\a\vs4\al\c1(2\b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,12)))＋\f(π,6)))，
所以只需将y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,6)))的图象向左平移eq \f(π,12)个单位长度就可以得到y＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,6)))的图象．
2．(2020·江苏)将函数y＝3sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,4)))的图象向右平移eq \f(π,6)个单位长度，则平移后的图象中与y轴最近的对称轴的方程是________．
答案 x＝－eq \f(5π,24)
解析 将函数y＝3sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,4)))的图象向右平移eq \f(π,6)个单位长度，
所得图象的函数解析式为
y＝3sineq \b\lc\[\rc\](\a\vs4\al\c1(2\b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,6)))＋\f(π,4)))＝3sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,12))).
令2x－eq \f(π,12)＝kπ＋eq \f(π,2)，k∈Z，
得对称轴的方程为x＝eq \f(kπ,2)＋eq \f(7π,24)，k∈Z，
分析知当k＝－1时，对称轴为直线x＝－eq \f(5π,24)，与y轴最近．
思维升华 (1)由y＝sin ωx的图象到y＝sin(ωx＋φ)的图象的变换：向左平移eq \f(φ,ω)(ω>0，φ>0)个单位长度而非φ个单位长度．
(2)如果平移前后两个图象对应的函数的名称不一致，那么应先利用诱导公式化为同名函数，ω为负时应先变成正值．
跟踪训练1 (1)(2020·天津)已知函数f(x)＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,3))).给出下列结论：
①f(x)的最小正周期为2π；
②f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)))是f(x)的最大值；
③把函数y＝sin x的图象上所有点向左平移eq \f(π,3)个单位长度，可得到函数y＝f(x)的图象．
其中所有正确结论的序号是( )
A．① B．①③ C．②③ D．①②③
答案 B
解析 T＝eq \f(2π,1)＝2π，故①正确．
当x＋eq \f(π,3)＝eq \f(π,2)＋2kπ(k∈Z)，
即x＝eq \f(π,6)＋2kπ(k∈Z)时，f(x)取得最大值，故②错误．
y＝sin x的图象eq \(――――――――→,\s\up11(向左平移\f(π,3)个单位长度))
y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,3)))的图象，故③正确．
(2)(2022·开封模拟)设ω>0，将函数y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(ωx＋\f(π,6)))的图象向右平移eq \f(π,6)个单位长度后，所得图象与原图象重合，则ω的最小值为( )
A．3 B．6 C．9 D．12
答案 D
解析 将函数y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(ωx＋\f(π,6)))的图象向右平移eq \f(π,6)个单位长度后，所得图象与原图象重合，
故eq \f(π,6)为函数y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(ωx＋\f(π,6)))的周期，
即eq \f(2kπ,ω)＝eq \f(π,6)(k∈N*)，
则ω＝12k(k∈N*)，
故当k＝1时，ω取得最小值12.
题型二 由图象确定y＝Asin(ωx＋φ)的解析式
例2 (1)(2022·安徽芜湖一中模拟)已知函数f(x)＝Acs(ωx＋φ)＋beq \b\lc\(\rc\)(\a\vs4\al\c1(A>0，ω>0，|φ|<\f(π,2)))
的大致图象如图所示，将函数f(x)的图象上点的横坐标拉伸为原来的3倍后，再向左平移eq \f(π,2)个单位长度，得到函数g(x)的图象，则函数g(x)的单调递增区间为( )
A.eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(3π,2)＋3kπ，3kπ))(k∈Z)
B.eq \b\lc\[\rc\](\a\vs4\al\c1(3kπ，3kπ＋\f(3π,2)))(k∈Z)
C.eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(7π,4)＋3kπ，－\f(π,4)＋3kπ))(k∈Z)
D.eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,4)＋3kπ，\f(5π,4)＋3kπ))(k∈Z)
答案 C
解析 依题意，eq \b\lc\{\rc\ (\a\vs4\al\c1(A＋b＝1，,－A＋b＝－3，))
解得eq \b\lc\{\rc\ (\a\vs4\al\c1(A＝2，,b＝－1，))
故f(x)＝2cs(ωx＋φ)－1，
而f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,12)))＝1，f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)))＝－1，
∴eq \f(T,4)＝eq \f(π,3)－eq \f(π,12)＝eq \f(π,4)，
故T＝π＝eq \f(2π,ω)，则ω＝2；
∴2cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)＋φ))－1＝1，
故eq \f(π,6)＋φ＝2kπ(k∈Z)，
又|φ|∴f(x)＝2cseq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,6)))－1；
将函数f(x)的图象上点的横坐标拉伸为原来的3倍后，
得到y＝2cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(2,3)x－\f(π,6)))－1，
再向左平移eq \f(π,2)个单位长度，
得到g(x)＝2cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(2,3)x＋\f(π,3)－\f(π,6)))－1
＝2cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(2,3)x＋\f(π,6)))－1，
令－π＋2kπ≤eq \f(2,3)x＋eq \f(π,6)≤2kπ(k∈Z)，
故－eq \f(7π,4)＋3kπ≤x≤－eq \f(π,4)＋3kπ(k∈Z)，故函数g(x)的单调递增区间为eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(7π,4)＋3kπ，－\f(π,4)＋3kπ))(k∈Z)．
(2)(2021·全国甲卷)已知函数f(x)＝2cs (ωx＋φ)的部分图象如图所示，则f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)))＝______.
答案 －eq \r(3)
解析 由题意可得，eq \f(3,4)T＝eq \f(13π,12)－eq \f(π,3)＝eq \f(3π,4)，
∴T＝π，ω＝eq \f(2π,T)＝2，
当x＝eq \f(13π,12)时，ωx＋φ＝2×eq \f(13π,12)＋φ＝2kπ，k∈Z，
∴φ＝2kπ－eq \f(13,6)π(k∈Z)．
令k＝1可得φ＝－eq \f(π,6)，
据此有f(x)＝2cseq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,6)))，
f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)))＝2cseq \b\lc\(\rc\)(\a\vs4\al\c1(2×\f(π,2)－\f(π,6)))＝2cseq \f(5π,6)＝－eq \r(3).
教师备选
1．(2022·天津中学月考)把函数f(x)图象上所有点的横坐标缩短到原来的eq \f(1,2)倍，纵坐标不变，再把所得曲线向右平移eq \f(π,4)个单位长度，得到函数g(x)的图象，已知函数g(x)＝Asin(ωx＋φ)eq \b\lc\(\rc\)(\a\vs4\al\c1(A>0，ω>0，|φ|<\f(π,2)))的部分图象如图所示，则f(x)等于( )
A．sineq \b\lc\(\rc\)(\a\vs4\al\c1(4x＋\f(π,3))) B．sineq \b\lc\(\rc\)(\a\vs4\al\c1(4x＋\f(π,6)))
C．sineq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,6))) D．sineq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,3)))
答案 D
解析 先根据函数图象求函数g(x)＝Asin(ωx＋φ)的解析式，
由振幅可得A＝1，
显然eq \f(T,4)＝eq \f(π,3)－eq \f(π,12)＝eq \f(π,4)，
所以T＝π，所以eq \f(2π,ω)＝π，所以ω＝2，
所以g(x)＝sin(2x＋φ)，
再由geq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,12)))＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)＋φ))＝0，
由|φ|所以g(x)＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,6)))，
反向移动先向左平移eq \f(π,4)个单位长度可得
sineq \b\lc\[\rc\](\a\vs4\al\c1(2\b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,4)))－\f(π,6)))＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,3)))，
再将横坐标伸长到原来的2倍可得
f(x)＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,3))).
2. 已知函数f(x)＝Acs(ωx＋φ)(A>0，ω>0,0<φ<π)为奇函数，该函数的部分图象如图所示，△EFG(点G是图象的最高点)是边长为2的等边三角形，则f(1)＝________.
答案 －eq \r(3)
解析 由题意得，A＝eq \r(3)，T＝4＝eq \f(2π,ω)，ω＝eq \f(π,2).
又因为f(x)＝Acs(ωx＋φ)为奇函数，
所以φ＝eq \f(π,2)＋kπ，k∈Z，由0<φ<π，取k＝0，
则φ＝eq \f(π,2)，
所以f(x)＝eq \r(3)cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)x＋\f(π,2)))，
所以f(1)＝－eq \r(3).
思维升华 确定y＝Asin(ωx＋φ)＋b(A>0，ω>0)的步骤和方法
(1)求A，b.确定函数的最大值M和最小值m，则A＝eq \f(M－m,2)，b＝eq \f(M＋m,2).
(2)求ω.确定函数的最小正周期T，则ω＝eq \f(2π,T).
(3)求φ，常用方法如下：把图象上的一个已知点代入(此时要注意该点在上升区间上还是在下降区间上)或把图象的最高点或最低点代入．
跟踪训练2 (1)(2020·全国Ⅰ改编)设函数f(x)＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(ωx＋\f(π,6)))在[－π，π]上的图象大致如图，则f(x)的解析式为( )
A．f(x)＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(3,2)x＋\f(π,6)))
B．f(x)＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3,2)x＋\f(π,6)))
C．f(x)＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3,4)x－\f(π,6)))
D．f(x)＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3,4)x＋\f(π,6)))
答案 B
解析 由图象知π所以1<|ω|<2.
因为图象过点eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(4π,9)，0))，
所以cseq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(4π,9)ω＋\f(π,6)))＝0，
所以－eq \f(4π,9)ω＋eq \f(π,6)＝kπ＋eq \f(π,2)，k∈Z，
所以ω＝－eq \f(9,4)k－eq \f(3,4)，k∈Z.
因为1<|ω|<2，
故k＝－1，得ω＝eq \f(3,2)，
所以f(x)＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3,2)x＋\f(π,6))).
(2)(2022·张家口市第一中学模拟)已知函数f(x)＝2sin(ωx＋φ)eq \b\lc\(\rc\)(\a\vs4\al\c1(ω>0，|φ|<\f(π,2)))的部分图象如图所示，则ω＝________，为了得到偶函数y＝g(x)的图象，至少要将函数y＝f(x)的图象向右平移________个单位长度．
答案 eq \f(π,8) 6
解析 由图象可知，函数f(x)的最小正周期为T＝2×[6－(－2)]＝16，
∴ω＝eq \f(2π,16)＝eq \f(π,8)，
则f(x)＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(πx,8)＋φ))，
由于函数f(x)的图象过点(－2,0)且在x＝－2附近单调递增，
∴－2×eq \f(π,8)＋φ＝2kπ(k∈Z)，
可得φ＝2kπ＋eq \f(π,4)(k∈Z)，
∵－eq \f(π,2)<φ∴φ＝eq \f(π,4)，
∴f(x)＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(πx,8)＋\f(π,4)))，
假设将函数f(x)的图象向右平移t个单位长度可得到偶函数g(x)的图象，
且g(x)＝f(x－t)＝2sineq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,8)x－t＋\f(π,4)))
＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,8)x－\f(πt,8)＋\f(π,4)))，
∴－eq \f(πt,8)＋eq \f(π,4)＝eq \f(π,2)＋kπ(k∈Z)，
解得t＝－2－8k(k∈Z)，
∵t>0，当k＝－1时，t取最小值6.
题型三 三角函数图象、性质的综合应用
命题点1 图象与性质的综合应用
例3 (2022·咸阳模拟)若函数f(x)＝2sin(ωx＋φ)eq \b\lc\(\rc\)(\a\vs4\al\c1(ω>0，|φ|<\f(π,2)))的最小正周期为π，且其图象向左平移eq \f(π,6)个单位长度后所得图象对应的函数g(x)为偶函数，则f(x)的图象( )
A．关于直线x＝eq \f(π,3)对称
B．关于点eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)，0))对称
C．关于直线x＝－eq \f(π,6)对称
D．关于点eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(5π,12)，0))对称
答案 D
解析 依题意可得ω＝eq \f(2π,π)＝2，
所以f(x)＝2sin(2x＋φ)，
所以f(x)的图象向左平移eq \f(π,6)个单位长度后所得图象对应的函数为g(x)＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,3)＋φ))，
又函数g(x)为偶函数，
所以eq \f(π,3)＋φ＝eq \f(π,2)＋kπ，k∈Z，
解得φ＝eq \f(π,6)＋kπ，k∈Z，
又|φ|所以φ＝eq \f(π,6)，
所以f(x)＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,6)))，
由2x＋eq \f(π,6)＝eq \f(π,2)＋kπ，k∈Z，得x＝eq \f(π,6)＋eq \f(kπ,2)，k∈Z，
所以f(x)图象的对称轴为x＝eq \f(π,6)＋eq \f(kπ,2)，k∈Z，
排除A，C，
由2x＋eq \f(π,6)＝kπ，k∈Z，得x＝－eq \f(π,12)＋eq \f(kπ,2)，k∈Z，
则f(x)图象的对称中心为eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,12)＋\f(kπ,2)，0))，k∈Z，排除B，
当k＝1时，－eq \f(π,12)＋eq \f(π,2)＝eq \f(5π,12)，故D正确．
命题点2 函数零点(方程根)问题
例4 已知关于x的方程2sin2x－eq \r(3)sin 2x＋m－1＝0在eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)，π))上有两个不同的实数根，则m的取值范围是____________．
答案 (－2，－1)
解析 方程2sin2x－eq \r(3)sin 2x＋m－1＝0可转化为
m＝1－2sin2x＋eq \r(3)sin 2x＝cs 2x＋eq \r(3)sin 2x
＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,6)))，x∈eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)，π)).
设2x＋eq \f(π,6)＝t，则t∈eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(7π,6)，\f(13π,6)))，
∴题目条件可转化为eq \f(m,2)＝sin t，t∈eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(7π,6)，\f(13π,6)))有两个不同的实数根．
∴y＝eq \f(m,2)和y＝sin t，t∈eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(7π,6)，\f(13π,6)))的图象有两个不同交点，如图：
由图象观察知，eq \f(m,2)的取值范围是eq \b\lc\(\rc\)(\a\vs4\al\c1(－1，－\f(1,2)))，
故m的取值范围是(－2，－1)．
延伸探究 本例中，若将“有两个不同的实数根”改成“有实根”，则m的取值范围是________．
答案 [－2,1)
解析 同例题知，eq \f(m,2)的取值范围是eq \b\lc\[\rc\)(\a\vs4\al\c1(－1，\f(1,2)))，
∴－2≤m<1，∴m的取值范围是[－2,1)．
命题点3 三角函数模型
例5 如图，一个大风车的半径为8 m，12 min旋转一周，它的最低点P0离地面2 m，风车翼片的一个端点P从P0开始按逆时针方向旋转，则点P离地面的距离h(m)与时间t(min)之间的函数关系式是( )
A．h(t)＝－8sin eq \f(π,6)t＋10
B．h(t)＝－cs eq \f(π,6)t＋10
C．h(t)＝－8sin eq \f(π,6)t＋8
D．h(t)＝－8cs eq \f(π,6)t＋10
答案 D
解析 设h＝Asin(ωt＋φ)＋B，
由题意可得hmax＝18，hmin＝2，T＝12，
∴A＝eq \f(hmax－hmin,2)＝8，B＝eq \f(hmax＋hmin,2)＝10，
ω＝eq \f(2π,T)＝eq \f(π,6)，h＝8sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)t＋φ))＋10，
当t＝0时，8sin φ＋10＝2，得sin φ＝－1，
可取φ＝－eq \f(π,2)，
∴h＝8sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)t－\f(π,2)))＋10＝－8cs eq \f(π,6)t＋10.
教师备选
(2022·福州模拟)如图所示，一半径为4米的水轮，水轮圆心O距离水面2米，已知水轮每60秒逆时针转动一圈，当水轮上点P从水中浮现时(图中点P0)开始计时，给出下列结论：
①点P第一次到达最高点需要20秒；
②当水轮转动155秒时，点P距离水面2米；
③当水轮转动50秒时，点P在水面下方，距离水面2米；
④点P距离水面的高度h(米)与t(秒)的函数解析式为h＝4cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,30)t＋\f(π,3)))＋2.
其中所有正确结论的序号是( )
A．①②③ B．①④
C．①②④ D．②③④
答案 A
解析 设点P距离水面的高度h(米)和时间t(秒)的函数解析式为
h＝Asin(ωt＋φ)＋Beq \b\lc\(\rc\)(\a\vs4\al\c1(A>0，ω>0，|φ|<\f(π,2)))，
由题意得eq \b\lc\{\rc\ (\a\vs4\al\c1(hmax＝A＋B＝6，,hmin＝－A＋B＝－2，,T＝\f(2π,ω)＝60，))
解得eq \b\lc\{\rc\ (\a\vs4\al\c1(A＝4，,B＝2，,ω＝\f(2π,T)＝\f(π,30)，))
又当t＝0时，h＝4sin φ＋2＝0eq \b\lc\(\rc\)(\a\vs4\al\c1(|φ|<\f(π,2)))，
解得φ＝－eq \f(π,6)，
故h＝4sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,30)t－\f(π,6)))＋2.故④错误；
对于①，令h＝6，即h＝4sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,30)t－\f(π,6)))＋2＝6，
解得t＝20，故①正确；
对于②，令t＝155，代入h＝4sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,30)t－\f(π,6)))＋2，
解得h＝2，故②正确；
对于③，令t＝50，代入h＝4sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,30)t－\f(π,6)))＋2，
解得h＝－2，故③正确．
思维升华 (1)研究y＝Asin(ωx＋φ)的性质时可将ωx＋φ视为一个整体，利用换元法和数形结合思想进行解题．
(2)方程根的个数可转化为两个函数图象的交点个数．
(3)三角函数模型的应用体现在两方面：一是已知函数模型求解数学问题；二是把实际问题抽象转化成数学问题，利用三角函数的有关知识解决问题．
跟踪训练3 (1)(2022·青岛模拟)已知函数f(x)＝cs 2xcs φ－sin 2xsin φeq \b\lc\(\rc\)(\a\vs4\al\c1(0<φ<\f(π,2)))的图象的一个对称中心为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)，0))，则下列说法不正确的是( )
A．直线x＝eq \f(5π,12)是函数f(x)的图象的一条对称轴
B．函数f(x)在eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(π,6)))上单调递减
C．函数f(x)的图象向右平移eq \f(π,6)个单位长度可得到y＝cs 2x的图象
D．函数f(x)在eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(π,2)))上的最小值为－1
答案 C
解析 ∵f(x)＝cs 2xcs φ－sin 2xsin φ
＝cs(2x＋φ)的图象的一个对称中心为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)，0))，
∴2×eq \f(π,6)＋φ＝eq \f(π,2)＋kπ，k∈Z，
∴φ＝eq \f(π,6)＋kπ，k∈Z.
∵0<φ∵f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(5π,12)))＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(2×\f(5π,12)＋\f(π,6)))＝cs π＝－1，
∴直线x＝eq \f(5π,12)是函数f(x)的图象的一条对称轴，故A正确；
当x∈eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(π,6)))时，2x＋eq \f(π,6)∈eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,6)，\f(π,2)))，
∴函数f(x)在eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(π,6)))上单调递减，故B正确；
函数f(x)的图象向右平移eq \f(π,6)个单位长度，
得到y＝cseq \b\lc\[\rc\](\a\vs4\al\c1(2\b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,6)))＋\f(π,6)))
＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,6)))的图象，故C错误；
当x∈eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(π,2)))时，2x＋eq \f(π,6)∈eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,6)，\f(7π,6)))，
∴函数f(x)在eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(π,2)))上的最小值为cs π＝－1，
故D正确．
(2)(2022·西南大学附中模拟)水车在古代是进行灌溉引水的工具，亦称“水转筒车”，是一种以水流作动力，取水灌田的工具．据史料记载，水车发明于隋而盛于唐，距今已有1 000多年的历史，是人类的一项古老的发明，也是人类利用自然和改造自然的象征，如图是一个半径为R的水车，一个水斗从点A(3，－3eq \r(3))出发，沿圆周按逆时针方向匀速旋转，且旋转一周用时120秒．经过t秒后，水斗旋转到P点，设点P的坐标为(x，y)，其纵坐标满足y＝f(t)＝Rsin(ωt＋φ)eq \b\lc\(\rc\)(\a\vs4\al\c1(t≥0，ω>0，|φ|<\f(π,2)))，则下列叙述正确的是( )
A．水斗作周期运动的初相为－eq \f(π,6)
B．在水斗开始旋转的60秒(含)中，其高度不断增加
C．在水斗开始旋转的60秒(含)中，其最高点离平衡位置的纵向距离是3eq \r(3)
D．当水斗旋转100秒时，其和初始点A的距离为6
答案 D
解析 对于A，由A(3，－3eq \r(3))，
知R＝eq \r(32＋－3\r(3)2)＝6，
又T＝120，所以ω＝eq \f(2π,T)＝eq \f(π,60).
当t＝0时，点P在点A位置，有－3eq \r(3)＝6sin φ，
解得sin φ＝－eq \f(\r(3),2)，
又|φ|所以φ＝－eq \f(π,3)，故A错误；
对于B，可知f(t)＝6sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,60)t－\f(π,3)))，
当t∈(0,60]时，eq \f(π,60)t－eq \f(π,3)∈eq \b\lc\(\rc\](\a\vs4\al\c1(－\f(π,3)，\f(2π,3)))，
所以函数f(t)先增后减，故B错误；
对于C，当t∈(0,60]时，
eq \f(π,60)t－eq \f(π,3)∈eq \b\lc\(\rc\](\a\vs4\al\c1(－\f(π,3)，\f(2π,3)))，sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,60)t－\f(π,3)))∈eq \b\lc\(\rc\](\a\vs4\al\c1(－\f(\r(3),2)，1))，
所以点P到x轴的距离的最大值为6，故C错误；
对于D，当t＝100时，eq \f(π,60)t－eq \f(π,3)＝eq \f(4π,3)，
P的纵坐标为y＝－3eq \r(3)，横坐标为x＝－3，
所以|PA|＝|－3－3|＝6，故D正确．
课时精练
1．函数f(x)＝－2cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)x＋\f(π,4)))的振幅、初相分别是( )
A．－2，eq \f(π,4) B．－2，－eq \f(π,4)
C．2，eq \f(π,4) D．2，－eq \f(π,4)
答案 C
解析 振幅为2，当x＝0时，φ＝eq \f(π,4)，即初相为eq \f(π,4).
2．将函数f(x)＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,4)))的图象，向右平移eq \f(π,4)个单位长度后得到函数g(x)的解析式为( )
A．g(x)＝sin 2x
B．g(x)＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,4)))
C．g(x)＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,4)))
D．g(x)＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(3π,4)))
答案 C
解析 向右平移eq \f(π,4)个单位长度后得，
g(x)＝sineq \b\lc\[\rc\](\a\vs4\al\c1(2\b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,4)))＋\f(π,4)))＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,4))).
3．(2022·郑州模拟)已知函数f(x)＝sin(ωx＋φ)eq \b\lc\(\rc\)(\a\vs4\al\c1(ω>0，|φ|<\f(π,2)))的最小正周期为π，将其图象向左平移eq \f(π,3)个单位长度后对应的函数为偶函数，则f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)))等于( )
A．－eq \f(1,2) B.eq \f(\r(3),2)
C．1 D.eq \f(1,2)
答案 D
解析 因为函数f(x)＝sin(ωx＋φ)的最小正周期为π，
所以ω＝eq \f(2π,π)＝2，
所以f(x)＝sin(2x＋φ)，
图象向左平移eq \f(π,3)个单位长度后所得函数为
y＝sineq \b\lc\[\rc\](\a\vs4\al\c1(2\b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,3)))＋φ))＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(2π,3)＋φ))，
因为y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(2π,3)＋φ))是偶函数，
所以eq \f(2π,3)＋φ＝eq \f(π,2)＋kπ(k∈Z)，
所以φ＝－eq \f(π,6)＋kπ(k∈Z)，
因为|φ|所以k＝0，φ＝－eq \f(π,6)，
所以f(x)＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,6)))，
所以f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)))＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2×\f(π,6)－\f(π,6)))＝sineq \f(π,6)＝eq \f(1,2).
4．(2022·天津五十七中月考)函数f(x)＝Asin(ωx＋φ)eq \b\lc\(\rc\)(\a\vs4\al\c1(A>0，ω>0，|φ|<\f(π,2)))的部分图象如图所示，将f(x)的图象上所有点的横坐标扩大到原来的4倍(纵坐标不变)，再把所得的图象沿x轴向左平移eq \f(π,3)个单位长度，得到函数g(x)的图象，则函数g(x)的一个单调递增区间为( )
A.eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(5π,3)，\f(π,3))) B.eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,3)，\f(7π,3)))
C.eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,4)，\f(3π,8))) D.eq \b\lc\[\rc\](\a\vs4\al\c1(\f(3π,8)，\f(π,2)))
答案 A
解析 根据函数f(x)＝Asin(ωx＋φ)eq \b\lc\(\rc\)(\a\vs4\al\c1(A>0，ω>0，|φ|<\f(π,2)))的部分图象，
可得A＝1，eq \f(1,2)·eq \f(2π,ω)＝eq \f(2π,3)－eq \f(π,6)，∴ω＝2.
结合“五点法”作图可得2×eq \f(π,6)＋φ＝eq \f(π,2)，
∴φ＝eq \f(π,6)，f(x)＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,6))).
将f(x)的图象上所有点的横坐标扩大到原来的4倍(纵坐标不变)，
可得y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)x＋\f(π,6)))的图象．
再把所得的图象沿x轴向左平移eq \f(π,3)个单位长度，
得到函数g(x)＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)x＋\f(π,6)＋\f(π,6)))
＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)x＋\f(π,3)))的图象．
令2kπ－eq \f(π,2)≤eq \f(1,2)x＋eq \f(π,3)≤2kπ＋eq \f(π,2)，k∈Z，
解得4kπ－eq \f(5π,3)≤x≤4kπ＋eq \f(π,3)，k∈Z，
可得函数g(x)的单调递增区间为eq \b\lc\[\rc\](\a\vs4\al\c1(4kπ－\f(5π,3)，4kπ＋\f(π,3)))，k∈Z，
令k＝0，可得一个单调递增区间为eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(5π,3)，\f(π,3))).
5．(2022·深圳模拟)设函数f(x)＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,3)))的图象为曲线E，则下列结论中正确的是( )
A.eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,12)，0))是曲线E的一个对称中心
B．若x1≠x2，且f(x1)＝f(x2)＝0，则|x1－x2|的最小值为eq \f(π,2)
C．将曲线y＝sin 2x向右平移eq \f(π,3)个单位长度，与曲线E重合
D．将曲线y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,3)))上各点的横坐标扩大到原来的2倍，纵坐标不变，与曲线E重合
答案 B
解析 函数f(x)＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,3)))的图象为曲线E，
令x＝－eq \f(π,12)，求得f(x)＝－1，为最小值，
故f(x)的图象关于直线x＝－eq \f(π,12)对称，故A错误；
若x1≠x2，且f(x1)＝f(x2)＝0，
则|x1－x2|的最小值为eq \f(T,2)＝eq \f(1,2)×eq \f(2π,2)＝eq \f(π,2)，故B正确；
将曲线y＝sin 2x向右平移eq \f(π,3)个单位长度，
可得y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(2π,3)))的图象，故C错误；
将曲线y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,3)))上各点的横坐标扩大到原来的2倍，纵坐标不变，可得y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)x－\f(π,3)))的图象，与曲线E不重合，故D错误．
6．已知函数f(x)＝2sin(ωx＋φ)eq \b\lc\(\rc\)(\a\vs4\al\c1(ω>0，|φ|≤\f(π,2)))图象的相邻两条对称轴间的距离为π，且对任意实数x，都有f(x)≤feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3))).将函数y＝f(x)的图象向左平移eq \f(π,6)个单位长度，得到函数y＝g(x)的图象，则关于函数y＝f(x)＋g(x)描述不正确的是( )
A．最小正周期是2π
B．最大值是eq \r(6)＋eq \r(2)
C．函数在eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(π,3)))上单调递增
D．图象关于直线x＝eq \f(π,4)对称
答案 C
解析 由条件知，函数f(x)的最小正周期T＝2π＝eq \f(2π,ω)，解得ω＝1.
因为f(x)max＝f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)))＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)＋φ))＝2，
即sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)＋φ))＝1，
则φ＝2kπ＋eq \f(π,6)，k∈Z.
因为|φ|≤eq \f(π,2)，
所以φ＝eq \f(π,6)，
所以f(x)＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,6)))，
g(x)＝f eq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,6)))＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,3)))，
则f(x)＋g(x)＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,6)))＋2sineq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,3)))
＝(eq \r(3)＋1)(sin x＋cs x)
＝(eq \r(6)＋eq \r(2))·sineq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,4)))，
根据正弦函数的图象和性质易知，
函数y＝(eq \r(6)＋eq \r(2))sineq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,4)))的最小正周期T＝2π，
函数最大值是eq \r(6)＋eq \r(2)，函数在eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(π,4)))上单调递增，在eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,4)，\f(π,3)))上单调递减，
图象关于直线x＝eq \f(π,4)对称，所以选项ABD正确，C错误．
7．(2022·北京丰台区模拟)将函数f(x)＝cs 2x的图象向左平移φ(φ>0)个单位长度，得到函数g(x)的图象．若函数g(x)的图象关于原点对称，则φ的一个取值为________．(答案不唯一)
答案 eq \f(π,4)
解析 将函数f(x)＝cs 2x的图象向左平移φ(φ>0)个单位长度，
可得g(x)＝cs(2x＋2φ)，由函数g(x)的图象关于原点对称，
可得g(0)＝cs 2φ＝0，
所以2φ＝eq \f(π,2)＋kπ，k∈Z，
φ＝eq \f(π,4)＋eq \f(kπ,2)，k∈Z，
当k＝0时，φ＝eq \f(π,4).
8．(2022·济南模拟)已知曲线C1：y＝cs x，C2：y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(2π,3)))，则为了得到曲线C1，首先要把C2上各点的横坐标变为原来的________倍，纵坐标不变，再把得到的曲线向右至少平移______个单位长度．(本题所填数字要求为正数)
答案 2 eq \f(π,6)
解析 ∵曲线C1：y＝cs x＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,2)))
＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2·\f(1,2)x＋\f(2π,3)－\f(π,6)))，
∴先将曲线C2上各点的横坐标变为原来的2倍，纵坐标不变，
再把得到的曲线y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2·\f(1,2)x＋\f(2π,3)))向右至少平移eq \f(π,6)个单位长度．
9．已知函数f(x)＝Asin(ωx＋φ)eq \b\lc\(\rc\)(\a\vs4\al\c1(A>0，ω>0，－\f(π,2)<φ<\f(π,2)))的最小正周期是π，且当x＝eq \f(π,6)时，f(x)取得最大值2.
(1)求f(x)的解析式；
(2)作出f(x)在[0，π]上的图象(要列表)；
(3)函数y＝f(x)的图象可由函数y＝sin x的图象经过怎样的变换得到？
解 (1)因为函数f(x)的最小正周期是π，
所以ω＝2.
又因为当x＝eq \f(π,6)时，
f(x)取得最大值2，所以A＝2，
同时2×eq \f(π,6)＋φ＝2kπ＋eq \f(π,2)，k∈Z，
φ＝2kπ＋eq \f(π,6)，k∈Z，
因为－eq \f(π,2)<φ所以φ＝eq \f(π,6)，所以f(x)＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,6))).
(2)因为x∈[0，π]，
所以2x＋eq \f(π,6)∈eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,6)，\f(13π,6))).
列表如下，
描点、连线得图象．
(3)将y＝sin x的图象上的所有点向左平移eq \f(π,6)个单位长度，得到函数y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,6)))的图象，
再将y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,6)))的图象上所有点的横坐标缩短到原来的eq \f(1,2)(纵坐标不变)，
得到函数y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,6)))的图象，
再将y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,6)))上所有点的纵坐标伸长2倍(横坐标不变)，
得到f(x)＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,6)))的图象．
10．(2022·普宁市第二中学模拟)已知向量m＝eq \b\lc\(\rc\)(\a\vs4\al\c1(sin x，－\f(1,2)))，n＝(eq \r(3)cs x，cs 2x)，函数f(x)＝m·n.
(1)求函数f(x)的最大值及最小正周期；
(2)将函数y＝f(x)的图象向左平移eq \f(π,6)个单位长度，得到函数y＝g(x)的图象，求g(x)在eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(π,2)))上的值域．
解 (1) f(x)＝m·n
＝eq \r(3)sin xcs x－eq \f(1,2)cs 2x
＝eq \f(\r(3),2)sin 2x－eq \f(1,2)cs 2x
＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,6))).
所以函数的最大值为1，最小正周期为
T＝eq \f(2π,|ω|)＝eq \f(2π,2)＝π.
(2)由(1)得f(x)＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,6))).
将函数y＝f(x)的图象向左平移eq \f(π,6)个单位长度后得到
y＝sineq \b\lc\[\rc\](\a\vs4\al\c1(2\b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,6)))－\f(π,6)))＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,6)))的图象．
因此g(x)＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,6)))，
又x∈eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(π,2)))，
所以2x＋eq \f(π,6)∈eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,6)，\f(7π,6)))，sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,6)))∈eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(1,2)，1)).
故g(x)在eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(π,2)))上的值域为eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(1,2)，1)).
11．函数f(x)＝Asin(ωx＋φ)＋b的图象如图，则f(x)的解析式和S＝f(0)＋f(1)＋f(2)＋…＋f(2 020)＋f(2 021)＋f(2 022)＋f(2 023)的值分别为( )
A．f(x)＝eq \f(1,2)sin 2πx＋1，S＝2 023
B．f(x)＝eq \f(1,2)sin 2πx＋1，S＝2 023eq \f(1,2)
C．f(x)＝eq \f(1,2)sineq \f(π,2)x＋1，S＝2 024eq \f(1,2)
D．f(x)＝eq \f(1,2)sineq \f(π,2)x＋1，S＝2 024
答案 D
解析 由图象知eq \b\lc\{\rc\ (\a\vs4\al\c1(A＋b＝\f(3,2)，,－A＋b＝\f(1,2)，又T＝4，))
∴ω＝eq \f(π,2)，b＝1，A＝eq \f(1,2)，
∴f(x)＝eq \f(1,2)sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)x＋φ))＋1.
由f(x)的图象过点eq \b\lc\(\rc\)(\a\vs4\al\c1(1，\f(3,2)))得
eq \f(1,2)sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)＋φ))＋1＝eq \f(3,2)，
∴cs φ＝1.
∴φ＝2kπ，k∈Z，取k＝0得φ＝0.
∴f(x)＝eq \f(1,2)sin eq \f(π,2)x＋1，
∴f(0)＋f(1)＋f(2)＋f(3)
＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)sin 0＋1))＋eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)sin \f(π,2)＋1))＋eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)sin π＋1))＋eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)sin \f(3π,2)＋1))＝4.
又2 024＝4×506，
∴S＝4×506＝2 024.
12．关于函数f(x)＝2cs2x－cseq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,2)))－1的描述正确的是( )
A．其图象可由y＝eq \r(2)sin 2x的图象向左平移eq \f(π,4)个单位长度得到
B．f(x)在eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,2)，0))上的最小值为－eq \r(2)
C．f(x)在eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(π,2)))上单调递增
D．f(x)在[0，π]上有3个零点
答案 B
解析 f(x)＝2cs2x－cseq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,2)))－1
＝sin 2x＋cs 2x＝eq \r(2)sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,4)))，
对于A，由y＝eq \r(2)sin 2x的图象向左平移eq \f(π,4)个单位长度，
得到y＝eq \r(2)sin 2eq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,4)))＝eq \r(2)sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,2)))
＝eq \r(2)cs 2x，
故选项A错误；
对于B，因为x∈eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,2)，0))，
所以2x＋eq \f(π,4)∈eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(3π,4)，\f(π,4)))，
所以sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,4)))∈eq \b\lc\[\rc\](\a\vs4\al\c1(－1，\f(\r(2),2)))，
所以f(x)∈eq \b\lc\[\rc\](\a\vs4\al\c1(－\r(2)，1))，
所以f(x)在eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,2)，0))上的最小值为－eq \r(2)，
故选项B正确；
对于C，令2kπ－eq \f(π,2)≤2x＋eq \f(π,4)≤2kπ＋eq \f(π,2)，k∈Z，
解得kπ－eq \f(3π,8)≤x≤kπ＋eq \f(π,8)，k∈Z，
所以f(x)的单调递增区间为eq \b\lc\[\rc\](\a\vs4\al\c1(kπ－\f(3π,8)，kπ＋\f(π,8)))，k∈Z，
所以f(x)在eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(π,8)))上单调递增，在eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,8)，\f(π,2)))上单调递减，故选项C错误；
对于D，令f(x)＝0，得2x＋eq \f(π,4)＝kπ，k∈Z，
解得x＝eq \f(kπ,2)－eq \f(π,8)，k∈Z，
因为x∈eq \b\lc\[\rc\](\a\vs4\al\c1(0，π))，
所以当k＝1时，x＝eq \f(3π,8)；
当k＝2时，x＝eq \f(7π,8)，所以f(x)在[0，π]上有2个零点，故选项D错误．
13．(2022·上海市吴淞中学月考)定义运算eq \b\lc\|\rc\|(\a\vs4\al\c1(\(\s\up7(a1),\s\d5(a3)) \(\s\up7(a2),\s\d5(a4))))＝a1a4－a2a3，将函数f(x)＝eq \b\lc\|\rc\|(\a\vs4\al\c1(\(\s\up7(\r(3)),\s\d5(1)) \(\s\up7(sin ωx),\s\d5(cs ωx))))(ω>0)的图象向左平移eq \f(2π,3)个单位长度，所得图象对应的函数为奇函数，则ω的最小值是________．
答案 eq \f(1,2)
解析 f(x)＝eq \r(3)cs ωx－sin ωx
＝－2sineq \b\lc\(\rc\)(\a\vs4\al\c1(ωx－\f(π,3)))，
图象向左平移eq \f(2π,3)个单位长度得，
g(x)＝－2sineq \b\lc\(\rc\)(\a\vs4\al\c1(ωx＋\f(2πω,3)－\f(π,3)))，
g(x)为奇函数，
则eq \f(2πω,3)－eq \f(π,3)＝kπ，k∈Z，
解得ω＝eq \f(1,2)＋eq \f(3,2)k，k∈Z，
所以ω的最小值为eq \f(1,2).
14．据市场调查，某种商品一年内每件出厂价在7千元的基础上，按月呈f(x)＝Asin(ωx＋φ)＋Beq \b\lc\(\rc\)(\a\vs4\al\c1(A>0，ω>0，|φ|<\f(π,2)))的模型波动(x为月份)，已知3月份达到最高价9 000元，9月份价格最低，为5 000元，则7月份的出厂价格为________元．
答案 6 000
解析 作出函数简图如图．
三角函数模型为y＝Asin(ωx＋φ)＋B，
由题意知A＝eq \f(1,2)×(9 000－5 000)＝2 000，
B＝eq \f(1,2)×(9 000＋5 000)＝7 000，
T＝2×(9－3)＝12，
∴ω＝eq \f(2π,T)＝eq \f(π,6).
将(3,9 000)看成函数图象的第二个特殊点，
则有eq \f(π,6)×3＋φ＝eq \f(π,2)，∴φ＝0，
故f(x)＝2 000sin eq \f(π,6)x＋7 000(1≤x≤12，x∈N*)．
∴f(7)＝2 000×sin eq \f(7π,6)＋7 000＝6 000(元)．
故7月份的出厂价格为6 000元．
15．将函数f(x)＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(ωx－\f(π,2)))(ω>0)的图象向右平移eq \f(π,2)个单位长度后得到函数g(x)的图象，且g(0)＝－1，则下列说法正确的有________(填序号)．
①g(x)为奇函数；
②geq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,2)))＝0；
③当ω＝5时，g(x)在(0，π)上有4个极值点；
④若g(x)在eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(π,5)))上单调递增，则ω的最大值为5.
答案 ②③④
解析 由题意得g(x)＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(ωx－\f(ωπ,2)－\f(π,2)))
＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(ωx－\f(ωπ,2))).
因为g(0)＝－1，所以sineq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(ωπ,2)))＝－1，
所以eq \f(ωπ,2)＝2kπ＋eq \f(π,2)，ω＝4k＋1，k∈N，
从而g(x)＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(ωx－2kπ－\f(π,2)))＝－cs ωx，
显然为偶函数，故①错误；
geq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,2)))＝－cs eq \f(4k＋1π,2)＝0，故②正确；
当ω＝5时，g(x)＝－cs 5x，
令g(x)＝－cs 5x＝±1得
5x＝kπ，x＝eq \f(kπ,5)，k∈Z.
因为016．(2022·河北武强中学模拟)已知函数f(x)＝Asin(ωx＋φ)，其中A>0，ω>0,0<φ<π，函数f(x)图象上相邻的两个对称中心之间的距离为eq \f(π,4)，且在x＝eq \f(π,3)处取到最小值－2.
(1)求函数f(x)的解析式；
(2)若将函数f(x)图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)，再向左平移eq \f(π,6)个单位长度，得到函数g(x)的图象，求函数g(x)的单调递增区间；
(3)若关于x的方程g(x)＝m＋2在x∈eq \b\lc\[\rc\)(\a\vs4\al\c1(0，\f(9π,8)))上有两个不同的实根，求实数m的取值范围．
解 (1)函数f(x)＝Asin(ωx＋φ)，
其中A>0，ω>0,0<φ<π，
由题知函数f(x)的最小正周期为eq \f(π,2)＝eq \f(2π,ω)，
解得ω＝4，
又函数f(x)在x＝eq \f(π,3)处取到最小值－2，
则A＝2，且f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)))＝－2，
即eq \f(4π,3)＋φ＝2kπ＋eq \f(3π,2)，k∈Z，
令k＝0可得φ＝eq \f(π,6)，
∴f(x)＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(4x＋\f(π,6))).
(2)函数f(x)＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(4x＋\f(π,6)))图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)，
得y＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,6)))，
再向左平移eq \f(π,6)个单位长度可得
g(x)＝2sineq \b\lc\[\rc\](\a\vs4\al\c1(2\b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,6)))＋\f(π,6)))＝2cs 2x，
令－π＋2kπ≤2x≤2kπ，k∈Z，
解得－eq \f(π,2)＋kπ≤x≤kπ，k∈Z，
∴g(x)的单调递增区间为eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,2)＋kπ，kπ))(k∈Z)．
(3)∵方程g(x)＝m＋2在x∈eq \b\lc\[\rc\)(\a\vs4\al\c1(0，\f(9π,8)))上有两个不同的实根，
作出函数g(x)＝2cs 2x，x∈eq \b\lc\[\rc\)(\a\vs4\al\c1(0，\f(9π,8)))的图象，
由图可知－2解得－4∴m的取值范围为－40，ω>0)，x≥0
振幅
周期
频率
相位
初相
A
T＝eq \f(2π,ω)
f＝eq \f(1,T)＝eq \f(ω,2π)
ωx＋φ
φ
ωx＋φ
0
eq \f(π,2)
π
eq \f(3π,2)
2π
x
eq \f(0－φ,ω)
eq \f(\f(π,2)－φ,ω)
eq \f(π－φ,ω)
eq \f(\f(3π,2)－φ,ω)
eq \f(2π－φ,ω)
y＝Asin(ωx＋φ)
0
A
0
－A
0
2x＋eq \f(π,6)
eq \f(π,6)
eq \f(π,2)
π
eq \f(3π,2)
2π
eq \f(13π,6)
x
0
eq \f(π,6)
eq \f(5π,12)
eq \f(2π,3)
eq \f(11π,12)
π
f(x)
1
2
0
－2
0
1