高考数学第一轮复习第十一章 §11.3　概率与统计的综合问题

这是一份高考数学第一轮复习第十一章 §11.3　概率与统计的综合问题，共15页。试卷主要包含了8，中位数为eq \f，111，，7，，75>10，829等内容，欢迎下载使用。
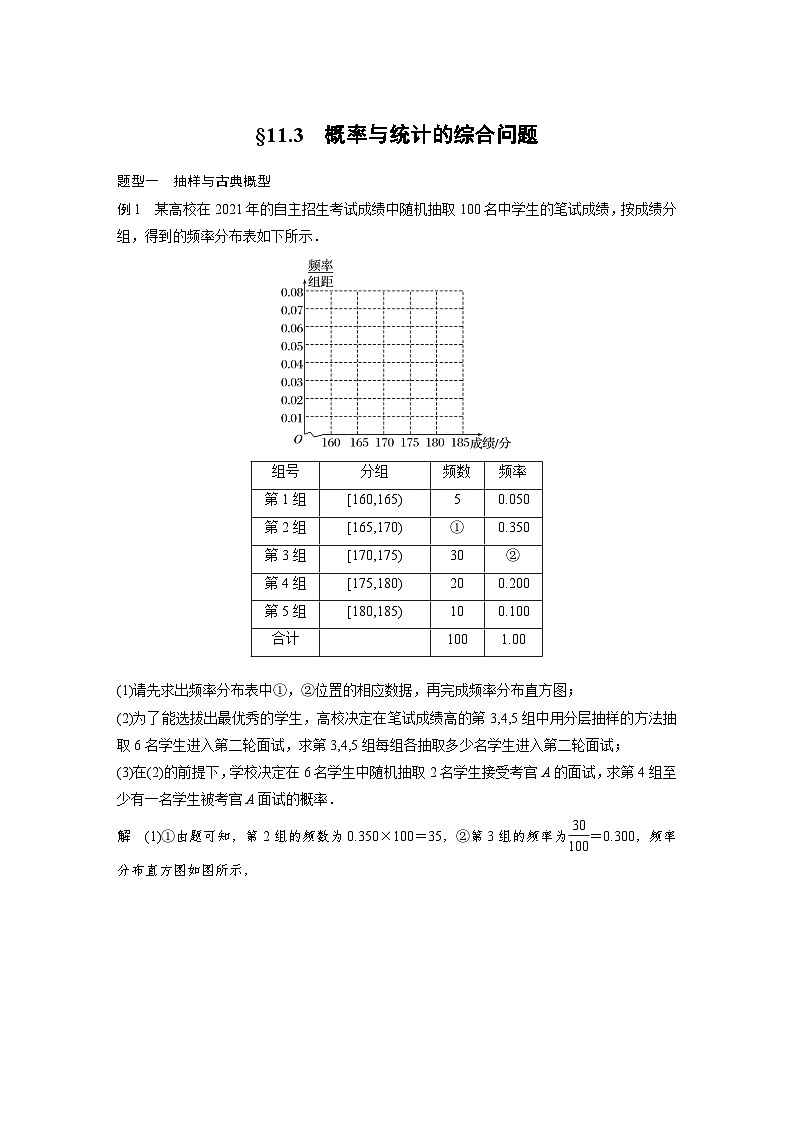
例1 某高校在2021年的自主招生考试成绩中随机抽取100名中学生的笔试成绩，按成绩分组，得到的频率分布表如下所示．
(1)请先求出频率分布表中①，②位置的相应数据，再完成频率分布直方图；
(2)为了能选拔出最优秀的学生，高校决定在笔试成绩高的第3,4,5组中用分层抽样的方法抽取6名学生进入第二轮面试，求第3,4,5组每组各抽取多少名学生进入第二轮面试；
(3)在(2)的前提下，学校决定在6名学生中随机抽取2名学生接受考官A的面试，求第4组至少有一名学生被考官A面试的概率．
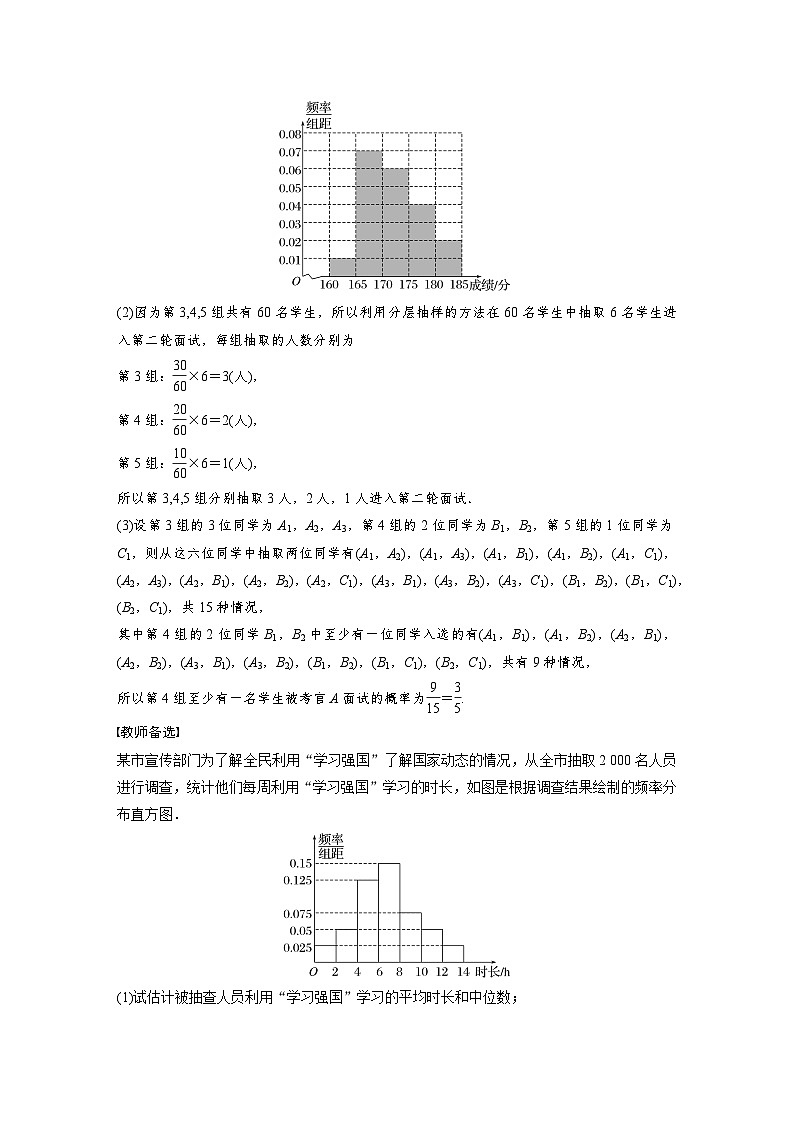
解 (1)①由题可知，第2组的频数为0.350×100＝35，②第3组的频率为eq \f(30,100)＝0.300，频率分布直方图如图所示，
(2)因为第3,4,5组共有60名学生，所以利用分层抽样的方法在60名学生中抽取6名学生进入第二轮面试，每组抽取的人数分别为
第3组：eq \f(30,60)×6＝3(人)，
第4组：eq \f(20,60)×6＝2(人)，
第5组：eq \f(10,60)×6＝1(人)，
所以第3,4,5组分别抽取3人，2人，1人进入第二轮面试．
(3)设第3组的3位同学为A1，A2，A3，第4组的2位同学为B1，B2，第5组的1位同学为C1，则从这六位同学中抽取两位同学有(A1，A2)，(A1，A3)，(A1，B1)，(A1，B2)，(A1，C1)，(A2，A3)，(A2，B1)，(A2，B2)，(A2，C1)，(A3，B1)，(A3，B2)，(A3，C1)，(B1，B2)，(B1，C1)，(B2，C1)，共15种情况，
其中第4组的2位同学B1，B2中至少有一位同学入选的有(A1，B1)，(A1，B2)，(A2，B1)，(A2，B2)，(A3，B1)，(A3，B2)，(B1，B2)，(B1，C1)，(B2，C1)，共有9种情况，
所以第4组至少有一名学生被考官A面试的概率为eq \f(9,15)＝eq \f(3,5).
教师备选
某市宣传部门为了解全民利用“学习强国”了解国家动态的情况，从全市抽取2 000名人员进行调查，统计他们每周利用“学习强国”学习的时长，如图是根据调查结果绘制的频率分布直方图．
(1)试估计被抽查人员利用“学习强国”学习的平均时长和中位数；
(2)宣传部为了解大家利用“学习强国”学习的具体情况，准备采用分层抽样的方法从学习时长在[8,10)和[10,12)内的人中选取50人了解情况，则应从两组中各选取多少人？再利用分层抽样的方法从选取的50人中选5人参加一个座谈会，现从参加座谈会的5人中随机选取2人发言，求学习时长在[10,12)内的人中至少有1人发言的概率．
解 (1)设被抽查人员利用“学习强国”学习的平均时长为eq \x\t(x)，中位数为y，
则eq \x\t(x)＝0.05×1＋0.1×3＋0.25×5＋0.3×7＋0.15×9＋0.1×11＋0.05×13＝6.8，
0．05＋0.1＋0.25＋0.15×(y－6)＝0.5，
解得y＝eq \f(20,3)，
所以估计被抽查人员利用“学习强国”学习的平均时长为6.8，中位数为eq \f(20,3).
(2)学习时长在[8,10)内的人数为2 000×0.15＝300，设选取的人数为a.学习时长在[10,12)内的人数为2 000×0.1＝200，设选取的人数为b.
则eq \f(a,300)＝eq \f(b,200)＝eq \f(50,500)，
解得a＝30，b＝20，
所以应从学习时长在[8,10)和[10,12)内的人中分别选取30人和20人．
若再从这50人中选取5人，则从学习时长在[8,10)内的人中选取3人，标记为A1，A2，A3，从学习时长在[10,12)内的人中选取2人，标记为B1，B2.
现从这5人中随机选取2人，则共有(A1，A2)，(A1，A3)，(A1，B1)，(A1，B2)，(A2，A3)，(A2，B1)，(A2，B2)，(A3，B1)，(A3，B2)，(B1，B2)10个基本事件，
其中事件“从学习时长在[10,12)内的人中至少选取1人”包含7个基本事件．
故学习时长在[10,12)内的人中至少有1人发言的概率为eq \f(7,10).
思维升华 解决抽样与古典概型的综合问题的方法
(1)定数，利用统计知识确定频数；(2)定型，根据事件“有限性和等可能性”判断是否为古典概型；(3)定性，由题意用列举的方法确定事件的基本事件数；(4)代入公式求解．
跟踪训练1 教育部《关于落实主体责任强化校园食品安全管理的指导意见》指出：非寄宿制中小学、幼儿园原则上不得在校内设置食品小卖部、超市，已经设置的，要逐步退出．为了了解学生对校内开设小卖部的意见，某校对65名住校生30天内在小卖部消费过的天数进行了统计，情况如下：
(1)用分层抽样的方法在消费天数不低于15天的住校生中选择6人进行意见调查，分别求其中消费天数在区间[15,20)，[20,25)，[25,30]内的人数；
(2)从(1)中选择的6人中任意抽取2人对取消校内小卖部给出具体意见，求这2人消费天数均在[25,30]内的概率．
解 (1)消费天数不低于15天的住校生共有18＋9＋27＝54(人)，
所以抽样比为eq \f(6,54)＝eq \f(1,9)，
消费天数在区间[15,20)内的人数为18×eq \f(1,9)＝2，
消费天数在区间[20,25)内的人数为9×eq \f(1,9)＝1，
消费天数在区间[25,30]内的人数为27×eq \f(1,9)＝3.
(2)分别记6名消费天数在区间[15,20)，[20,25)，[25,30]内的住校生为a1，a2，b，c1，c2，c3，从中任取2人有
(a1，a2)，(a1，b)，(a1，c1)，(a1，c2)，(a1，c3)，(a2，b)，(a2，c1)，(a2，c2)，(a2，c3)，(b，c1)，(b，c2)，(b，c3)，(c1，c2)，(c1，c3)，(c2，c3)共15种情况，
其中这2人消费天数均在[25,30]内的有(c1，c2)，(c1，c3)，(c2，c3)共3种情况，
故这2人消费天数均在[25,30]内的概率为eq \f(3,15)＝eq \f(1,5).
题型二 茎叶图与概率的综合
例2 (2022·鹰潭模拟)第24届冬季奥林匹克运动会于2022年2月在中国北京举行．为迎接此次冬奥会，北京市组织大学生开展冬奥会志愿者的培训活动，并在培训结束后统一进行了一次考核．为了了解本次培训活动的效果，从A，B两所大学各随机抽取10名学生的考核成绩，并作出如图所示的茎叶图．
(1)计算A，B两所大学学生的考核成绩的平均值；
(2)由茎叶图判断A，B两所大学学生考核成绩的稳定性；(不用计算)
(3)将学生的考核成绩分为两个等级，如下表所示．现从样本考核等级为优秀的学生中任取2人，求2人来自同一所大学的概率．
解 (1)eq \x\t(x)A＝
eq \f(64＋75＋78＋78＋79＋72＋85＋86＋91＋92,10)
＝eq \f(800,10)＝80，
eq \x\t(x)B＝eq \f(67＋62＋70＋79＋78＋87＋84＋85＋95＋93,10)＝eq \f(800,10)＝80.
(2)由茎叶图可知，A所大学学生的成绩比B所大学学生的成绩稳定．
(3)记事件M为“从样本考核等级为优秀的学生中任取2人，2人来自同一所大学”．样本中，A校考核等级为优秀的学生共有3人，分别记为a，b，c，B校考核等级为优秀的学生共有3人，分别记为A，B，C，从这6人中任取2人，所有的基本事件为ab，ac，aA，aB，aC，bc，bA，bB，bC，cA，cB，cC，AB，AC，BC共15个，而事件M包含的基本事件是ab，ac，bc，AB，AC，BC共6个，
因此P(M)＝eq \f(6,15)＝eq \f(2,5).
教师备选
(2022·萍乡模拟)某中学高三共有男生800人，女生1 200人．现学校某兴趣小组为研究学生日均消费水平是否与性别有关，采用分层抽样的方式从高三年级抽取男女生若干人．记录其日均消费，得到如图所示男生日均消费的茎叶图和女生日均消费的频率分布直方图．将所抽取的女生的日均消费分为以下五组：(15,20]，(20,25]，(25,30]，(30,35]，(35,40]，规定日均消费不超过25元的人为“节俭之星”．
(1)请完成下面2×2的列联表；
根据以上2×2的列联表，能否有90%的把握认为学生是否为“节俭之星”与性别有关？
(2)现已知学校某小组有6名“节俭之星”，其中男生2人，女生4人．现从中选取2人在学校做勤俭节约宣讲活动报告，求选取的2人中至少有一名男生的概率．
附：K2＝eq \f(nad－bc2,a＋bc＋da＋cb＋d)，其中n＝a＋b＋c＋d.
解 (1)由茎叶图可知此次抽样男生共20人，由于采用分层抽样的方式，抽取女生为30人．依题意，男“节俭之星”共7人，女“节俭之星”共18人，填表如下：
从而K2＝eq \f(50×18×13－12×72,25×25×20×30)＝3.000>2.706，
故有90%的把握认为学生是否为“节俭之星”与性别有关．
(2)记2名男生分别为A1，A2，记4名女生分别为B1，B2，B3，B4，则从这6名“节俭之星”选取2名的所有可能有(A1，A2)，(A1，B1)，(A1，B2)，(A1，B3)，(A1，B4)，(A2，B1)，(A2，B2)，(A2，B3)，(A2，B4)，(B1，B2)，(B1，B3)，(B1，B4)，(B2，B3)，(B2，B4)，(B3，B4)，共15种，其中至少有1名男生的情况有9种，
因此，所求概率为P＝eq \f(3,5).
思维升华 在统计中，一些问题可以通过图表获取信息，然后利用这些信息进行计算．
跟踪训练2 (2022·安庆模拟)某中学高一年级从甲、乙两个班级各选出7名学生参加学科测试，他们取得的成绩的茎叶图如图，其中甲班学生的平均分是85，乙班学生成绩的中位数是83.
(1)求x和y的值，并计算甲班7位学生成绩的方差s2；
(2)从成绩在90分以上的学生中随机抽取两名学生，求至少有一名学生是甲班的概率．
解 (1)由题意知85×7＝79＋78＋80＋80＋x＋85＋92＋96，解得x＝5.
又因为乙班学生成绩的中位数是83，所以y＝3.
s2＝eq \f(1,7)[(79－85)2＋(78－85)2＋(80－85)2＋(85－85)2＋(85－85)2＋(92－85)2＋(96－85)2]＝40.
(2)设甲班成绩在90分以上的学生为A，B，
乙班成绩在90分以上的学生为C，D，E.
从成绩在90分以上的学生中随机抽取两名学生，
共有AB，AC，AD，AE，BC，BD，BE，CD，CE，DE,10种情况，其中至少有一名学生是甲班的学生共有7种情况，
记“至少有一名学生是甲班的学生”为事件M，
则P(M)＝eq \f(7,10).
题型三 频率分布直方图与独立性检验
例3 (2022·齐齐哈尔模拟)已知某体育学校有学生2 000人，其中男生1 200人，女生800人．现按性别采用分层抽样的方法抽取了200名学生，并记录他们每天的平均跑步时间(单位：min)得到如下频率分布表：
(1)根据频率分布表，求实数m，n，p的值，完成如图所示的频率分布直方图；
(2)若在被抽取的200名学生中有100名男生每天的平均跑步时间不低于40 min，完成下列2×2列联表，能否在犯错误的概率不超过0.001的情况下，认为该学校学生每天的平均跑步时间不低于40 min与性别有关？
附：K2＝eq \f(nad－bc2,a＋bc＋da＋cb＋d)，其中n＝a＋b＋c＋d.
解 (1)n＝1－0.05－0.20－0.15－0.25－0.05＝0.30，
p＝200×0.30＝60，
m＝200×0.20＝40，
频率分布直方图如图．
(2)2×2列联表：
所以K2＝eq \f(200×20×50－30×1002,50×150×80×120)≈11.111，
又因为11.111>10.828，
所以能在犯错误的概率不超过0.001的情况下认为该校学生每天的平均跑步时间不低于40 min与性别有关．
教师备选
(2022·广元模拟)某中学调查了该校某班全部40名同学参加棋艺社团和武术社团的情况，数据如下表：(单位：人)
(1)能否有95%的把握认为参加棋艺社团和参加武术社团有关？
(2)已知在参加武术社团且未参加棋艺社团的10人中，从2到11进行编号，从中抽取一人．先后两次抛掷一枚骰子，出现的点数之和为被抽取的序号，试求抽到6号或7号的概率．
附：K2＝eq \f(nad－bc2,a＋bc＋da＋cb＋d)，其中n＝a＋b＋c＋d.
解 (1)由K2＝eq \f(40×8×15－7×102,15×25×22×18)≈0.673 4，
则K26.635，
∴有99%的把握认为该企业生产的这种产品的质量指标值与设备改造有关．
(2)用频率估计概率，1 000件产品中大约有960件合格品，40件不合格品，
则获利约为180×960－100×40＝168 800(元)，
因此，该企业大约能获利168 800元．
课时精练
1．(2022·东三省四市联考)在一个文艺比赛中，5名专业人士和5名观众代表各组成一个评委小组，给参赛选手打分．下面是两组评委对同一名选手的打分：
(1)请判断小组A与小组B哪一个更像是由专业人士组成的？
(2)若从A组的5位评委中任选2名评委，求其中恰有一位评委打分为95分的概率．
解 (1)由表格数据，知
eq \x\t(x)A＝eq \f(92＋95＋93＋95＋90,5)＝93，
eq \x\t(x)B＝eq \f(98＋80＋90＋85＋97,5)＝90，
∴seq \\al(2,A)＝eq \f(1,5)eq \i\su(i＝1,5, )(xAi－eq \x\t(x)A)2＝3.6b，))
解得a＝400，b＝100.
(2)由题意可知，在抽取的5人中，有3人是消费主力军，分别记为a1，a2，a3，有2人是消费潜力军，分别记为b1，b2.记“这2人中至少有一人是消费潜力军”为事件A.
从这5人中抽取2人所有可能的情况为(a1，a2)，(a1，a3)，(a1，b1)，(a1，b2)，(a2，a3)，(a2，b1)，(a2，b2)，(a3，b1)，(a3，b2)，(b1，b2)，共10种．
符合事件A的有(a1，b1)，(a1，b2)，(a2，b1)，(a2，b2)，(a3，b1)，(a3，b2)，(b1，b2)，共7种．
故所求概率为P(A)＝eq \f(7,10).
3．(2022·毕节模拟)某校为了解同学们选择“网页制作”选修课的情况，随机调查文、理科同学各50名，每位同学对是否选择这门课程做出“选择”和“不选择”的答案，统计得如下列联表：
(1)完成列联表，判断是否有95%的把握认为选择“网页制作”选修课与文、理科类别有关？
(2)从文科同学中按分层抽样的方法选取5人，再从这5人中任选3人，求这3人中至多有1人不选择“网页制作”选修课的概率．
附：K2＝eq \f(nad－bc2,a＋bc＋da＋cb＋d)，其中n＝a＋b＋c＋d.
解 (1)列联表为
K2＝eq \f(100×40×20－30×102,50×50×30×70)＝eq \f(100,21)>3.841，
∴有95%的把握认为选择“网页制作”选修课与文、理科类别有关．
(2)由题意得，5名文科同学中有3人做出“选择”，设为A1，A2，A3；有2人“不选择”，
设为B1，B2，从中选3人的总体情况有
A1A2A3，A1A2B1，A1A2B2，A1A3B1，A1A3B2，A1B1B2，A2A3B1，A2A3B2，A2B1B2，A3B1B2，共10种，
至多有1人不选择“网页制作”选修课有7种，
∴概率为P＝eq \f(7,10).
4．近年来，国资委、党委高度重视扶贫开发工作，坚决贯彻落实中央扶贫工作重大决策部署，在各个贫困县全力推进定点扶贫各项工作，取得了积极成效，某贫困县为了响应国家精准扶贫的号召，特地承包了一块土地，已知土地的使用面积以及相应的管理时间的关系如下表所示：
并调查了某村300名村民参与管理的意愿，得到的部分数据如下表所示：
(1)求y关于x的线性回归方程；(计算结果保留两位小数)
(2)是否有99.9%的把握认为村民的性别与参与管理的意愿具有相关性？
参考公式：eq \(b,\s\up6(^))＝eq \f(\i\su(i＝1,n, )xi－\x\t(x)yi－\x\t(y),\i\su(i＝1,n, )xi－\x\t(x)2)，eq \(a,\s\up6(^))＝eq \x\t(y)－eq \(b,\s\up6(^))eq \x\t(x)，K2＝eq \f(nad－bc2,a＋bc＋da＋cb＋d)，
其中n＝a＋b＋c＋d.
临界值表：
解 (1)依题意得，eq \x\t(x)＝eq \f(1＋2＋3＋4＋5,5)＝3，
eq \x\t(y)＝eq \f(8＋10＋13＋25＋24,5)＝16，
故eq \i\su(i＝1,5, )(xi－eq \x\t(x))(yi－eq \x\t(y))＝(－2)×(－8)＋(－1)×(－6)＋1×9＋2×8＝47，
eq \i\su(i＝1,5, )(xi－eq \x\t(x))2＝4＋1＋1＋4＝10,
则eq \(b,\s\up6(^))＝eq \f(\(∑,\s\up6(5),\s\d5(i＝1)) xi－\x\t(x)yi－\x\t(y),\(∑,\s\up6(5),\s\d5(i＝1))xi－\x\t(x)2)＝eq \f(47,10)＝4.7，
eq \(a,\s\up6(^))＝eq \x\t(y)－eq \(b,\s\up6(^))eq \x\t(x)＝16－4.7×3＝1.9，
所以y关于x的线性回归方程为eq \(y,\s\up6(^))＝4.7x＋1.9.
(2)依题意，女性不愿意参与管理的人数为50，
计算得K2的观测值为
k＝eq \f(300×150×50－50×502,200×100×200×100)
＝eq \f(300×5 000×5 000,200×100×200×100)＝18.75>10.828，
故有99.9%的把握认为村民的性别与参与管理的意愿具有相关性．
5．(2022·开封模拟)人耳的听力情况可以用电子测听器检测，正常人听力的等级为0～25 dB(分贝)，并规定测试值在区间(0,5]为非常优秀，测试值在区间(5,10]为优秀．某校500名同学参加了听力测试，从中随机抽取了50名同学的测试值作为样本，制成如下频率分布直方图：
(1)从总体的500名学生中随机抽取1人，估计其测试值在区间(0,10]内的概率；
(2)已知样本中听力非常优秀的学生有4人，估计总体中听力为优秀的学生人数；
(3)现选出一名同学参加另一项测试，测试规则如下：四个音叉的发音情况不同，由强到弱的编号分别为1,2,3,4.测试前将音叉顺序随机打乱，被测试的同学依次听完后，将四个音叉按发音由强到弱重新排序，所对应的音叉编号分别为a1，a2，a3，a4(其中集合{a1，a2，a3，a4}＝{1,2,3,4})．记Y＝|1－a1|＋|2－a2|＋|3－a3|＋|4－a4|，可用Y描述被测试者的听力偏离程度，求Y≤2的概率．
解 (1)根据频率分布直方图知，样本中测试值在区间(0,10]内的频率为1－(0.06＋0.08＋0.02)×5＝1－0.8＝0.2，
以频率为概率，从总体的500名学生中随机抽取1人，估计其测试值在区间(0,10]内的概率为0.2.
(2)由(1)知，样本中听力为优秀的学生人数为0.2×50－4＝6，
∴估计总体中听力为优秀的学生人数为
500×eq \f(6,50)＝60.
(3)当a1＝1时，序号a1，a2，a3，a4的情况为6种，
分别记为(1,2,3,4)，(1,2,4,3)，(1,3,2,4)，(1,3,4,2)，(1,4,2,3)，(1,4,3,2)，
同理，当a1＝2,3,4时，序号a1，a2，a3，a4的情况也分别为6种，
∴序号a1，a2，a3，a4所有的情况总数为24种．
当Y＝0时，a1＝1，a2＝2，a3＝3，a4＝4，
当Y＝|1－a1|＋|2－a2|＋|3－a3|＋|4－a4|＝2时，a1，a2，a3，a4的取值为a1＝1，a2＝2，a3＝4，a4＝3，
或a1＝1，a2＝3，a3＝2，a4＝4，或a1＝2，a2＝1，a3＝3，a4＝4，
∴当Y≤2时，序号a1，a2，a3，a4对应的情况为4种，即P(Y≤2)＝eq \f(4,24)＝eq \f(1,6).组号
分组
频数
频率
第1组
[160,165)
5
0.050
第2组
[165,170)
①
0.350
第3组
[170,175)
30
②
第4组
[175,180)
20
0.200
第5组
[180,185)
10
0.100
合计
100
1.00
天数
[5,10)
[10,15)
[15,20)
[20,25)
[25,30]
人数
4
7
18
9
27
考核成绩
[60,85]
[86,100]
考核等级
合格
优秀
“节俭之星”
非“节俭之星”
总计
男生
女生
总计
P(K2≥k0)
0.15
0.10
0.05
0.025
0.01
0.005
k0
2.072
2.706
3.841
5.024
6.635
7.829
“节俭之星”
非“节俭之星”
总计
男生
7
13
20
女生
18
12
30
总计
25
25
50
每天平均跑步时间/min
频数
频率
[0,20)
10
0.05
[20,40)
m
0.20
[40,60)
30
0.15
[60,80)
50
0.25
[80,100)
p
n
[100,120]
10
0.05
合计
200
1
男生
女生
总计
每天平均跑步时间低于40 min
每天平均跑步时间不低于40 min
总计
P(K2≥k0)
0.15
0.10
0.05
0.025
0.01
0.001
k0
2.072
2.706
3.841
5.024
6.635
10.828
男生
女生
总计
每天平均跑步时间低于40 min
20
30
50
每天平均跑步时间不低于40 min
100
50
150
总计
120
80
200
参加棋艺社团
未参加棋艺社团
参加武术社团
8
10
未参加武术社团
7
15
P(K2≥k0)
0.10
0.05
0.025
k0
2.706
3.841
5.024
质量指示值
[15，20)
[20，25)
[25，30)
[30，35)
[35，40)
[40，45]
频数
4
36
96
28
32
4
设备改造前
设备改造后
总计
合格品
不合格品
总计
P(K2≥k0)
0.150
0.100
0.050
0.025
0.010
k0
2.072
2.706
3.841
5.024
6.635
设备改造前
设备改造后
总计
合格品
172
192
364
不合格品
28
8
36
总计
200
200
400
小组A
92
95
93
95
90
小组B
98
80
90
85
97
年龄
[10，20)
[20，30)
[30，40)
[40，50)
[50，60)
[60，70)
人数
100
150
a
200
b
50
选择
不选择
总计
理科
40
文科
20
总计
P(K2≥k0)
0.050
0.010
0.001
k0
3.841
6.635
10.828
选择
不选择
总计
理科
40
10
50
文科
30
20
50
总计
70
30
100
土地使用面积x(单位：亩)
1
2
3
4
5
管理时间y(单位：月)
8
10
13
25
24
愿意参与管理
不愿意参与管理
男性村民
150
50
女性村民
50
P(K2≥k0)
0.100
0.050
0.025
0.010
0.001
k0
2.706
3.841
5.024
6.635
10.828