2022-2023学年四川省达州外国语学校七年级（上）期末数学试卷（含解析）

这是一份2022-2023学年四川省达州外国语学校七年级（上）期末数学试卷（含解析），共16页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。
2022-2023学年四川省达州外国语学校七年级（上）期末数学试卷一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）1.下列式子正确的是(    )A.  B.  C.  D. 2.如图，一个几何体由个大小相同、棱长为的小正方体搭成，下列关于这个几何体的说法正确的是(    )

 A. 主视图的面积为 B. 左视图的面积为
C. 俯视图的面积为 D. 三种视图的面积都是3.以下问题，适合用普查的是(    )A. 调查某种灯泡的使用寿命 B. 调查中央电视台春节联欢会的收视率
C. 调查我国八年级学生的视力情况 D. 调查你们班学生早餐是否有喝牛奶的习惯4.下列说法中正确的是(    )A. 的次数是 B. 是单项式
C. 是单项式 D. 的系数是5.如图，数轴上、、、四点对应的整数分别是、、、，且有，那么，原点应是点(    )
A.  B.  C.  D. 6.如果方程与方程的解相同，则的值为(    )A.  B.  C.  D. 7.已知和是同类项，则的值是(    )A.  B.  C.  D. 8.已知，，三点在同一条直线上，，分别为线段，的中点，且，，则的长为(    )A.  B.  C. 或 D. 或9.过某个多边形一个顶点的所有对角线，把这个多边形分成个三角形，这个多边形是(    )A.  B.  C.  D. 10.中国古代问题：有甲、乙两个牧童，甲对乙说：“把你的羊给我一只，我的羊数就是你的羊数的倍”。乙回答说：“最好还是把你的羊给我一只，我们羊数就一样了”。若设甲有只羊，则下列方程正确的是(    )A.  B.
C.  D. 二、填空题（本大题共6小题，共18.0分）11.若与的和是单项式，则的值为______ ．12.若，则 ______ ．13.关于的方程的解是，则______．14.一个正方体的表面展开图如图所示，这个正方体的每一个面上都填有一个数字，且各相对面上所填的数字互为倒数，则的值为______ ．
 15.设，其中，，为常数，已知当时，；则当时， ______ ．16.已知整数，，，满足下列条件：，，，依此类推，则的值等于______ ．三、计算题（本大题共1小题，共8.0分）17.解方程
                    
．四、解答题（本大题共8小题，共64.0分。解答应写出文字说明，证明过程或演算步骤）18.本小题分
计算：
；
．19.本小题分
先化简下式，再求值：，其中20.本小题分
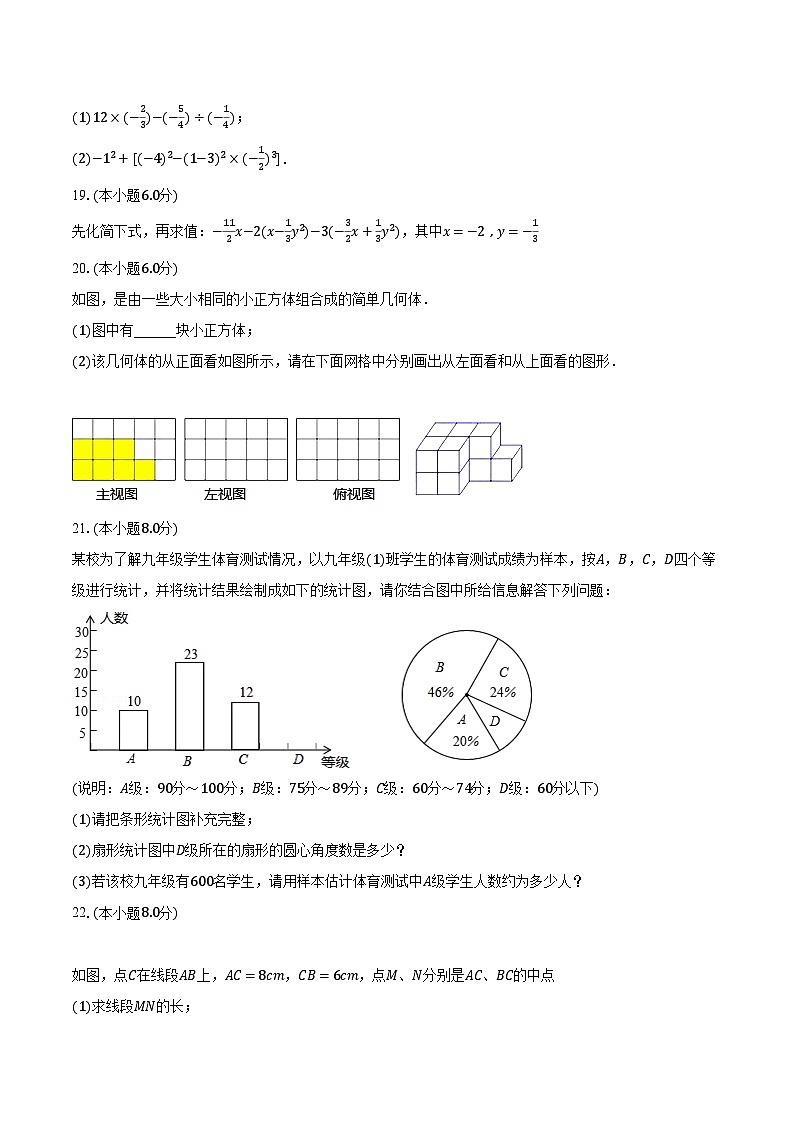
如图，是由一些大小相同的小正方体组合成的简单几何体．
图中有______块小正方体；
该几何体的从正面看如图所示，请在下面网格中分别画出从左面看和从上面看的图形．

 21.本小题分
某校为了解九年级学生体育测试情况，以九年级班学生的体育测试成绩为样本，按，，，四个等级进行统计，并将统计结果绘制成如下的统计图，请你结合图中所给信息解答下列问题：

说明：级：分分；级：分分；级：分分；级：分以下
请把条形统计图补充完整；
扇形统计图中级所在的扇形的圆心角度数是多少？
若该校九年级有名学生，请用样本估计体育测试中级学生人数约为多少人？22.本小题分

如图，点在线段上，，，点、分别是、的中点
求线段的长；
若为线段上任意一点，满足，其他条件不变，你能猜出线段的长度吗？并说明理由．
23.本小题分
已知：线段．
 如图，点沿线段自点向点以厘米秒运动，点出发秒后，点沿线段自点向点以厘米秒运动，问再经过几秒后、相距？
 如图：，，，点绕着点以度秒的速度逆时针旋转一周停止，同时点沿直线自点向点运动，假若点、两点能相遇，求点运动的速度．

 24.本小题分
某超市第一次用元购进，两种商品，其中购进商品的件数比购进商品件数的倍多件，，两种商品的进价和售价如下表注：获利售价进价  进价元件售价元件该超市第一次购进，两种商品各多少件？
该超市将第一次购进的，两种商品全部销售完后一共可获得多少利润？
该超市第二次以第一次的进价又购进，两种商品其中购进商品的件数不变，购进商品的件数是第一次购进商品件数的倍商品按原价销售，商品打折销售第二次购进的、两种商品销售完后获得的总利润比第一次获得的总利润多元，求第二次商品是按原售价打几折销售的．25.本小题分
将正方形如图作如下划分：
第次划分：分别连接正方形对边的中点如图，得线段和，它们交于点，此时图中共有个正方形；
第次划分：将图左上角正方形再作划分，得图，则图中共有个正方形；
若每次都把左上角的正方形一次划分下去，则第次划分后，图中共有______ 个正方形；
继续划分下去，第几次划分后能有个正方形？写出计算过程．
能否将正方形性划分成有个正方形的图形？如果能，请算出是第几次划分，如果不能，需说明理由．
如果设原正方形的边长为，通过不断地分割该面积为的正方形，并把数量关系和几何图形巧妙地结合起来，可以很容易得到一些计算结果，试着探究求出下面表达式的结果吧．
计算直接写出答案即可


答案和解析 1.【答案】 【解析】解：、，故A错误；
B、，故B错误；
C、，故C错误；
D、，故D正确；
故选：．
根据正数大于零，零大于负数，可得答案．
本题考查了有理数大小比较，利用正数大于零，零大于负数是解题关键．2.【答案】 【解析】【分析】
本题主要考查了几何体的三种视图面积的求法及比较，关键是掌握三视图的画法．
主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形，看分别得到几个面，比较即可．
【解答】
解：、从正面看，可以看到个正方形，面积为，故A选项错误；
B、从左面看，可以看到个正方形，面积为，故B选项正确；
C、从上面看，可以看到个正方形，面积为，故C选项错误；
D、三种视图的面积不相同，故D选项错误．
故选：．3.【答案】 【解析】解：、调查某种灯泡的使用寿命，不能使用普查，错误；
B、调查中央电视台春节联欢会的收视率被调查的对象都较大，不能使用普查，错误；
C、调查我国八年级学生的视力情况被调查的对象都较大，不能使用普查，错误；
D、调查你们班学生早餐是否有喝牛奶的习惯被调查的对象较小，故D宜使用普查；
故选：．
根据被调查对象较小时，宜使用普查，可得答案．
本题考查了全面调查与抽样调查，被调查对象较小时宜使用普查．4.【答案】 【解析】解：、的次数是，故A错误；
B、是分式，故B错误；
C、是单项式，故C正确；
D、的系数是，故D错误；
故选：．
根据单项式是数与字母的乘积，单项式的次数是字母指数和，单项式的系数是数字因数，可得答案．
本题考查了单项式，单项式是数与字母的乘积，单项式的次数是字母指数和，单项式的系数是数字因数，注意是常数不是字母．5.【答案】 【解析】解：由数轴可得，
若原点在点，则，
若原点在点，则，
若原点在点，则，
若原点在点，则，
数轴上、、、四点对应的整数分别是、、、，且有，
原点应是点。
故选：。
根据数轴可以分别假设原点在、、、，然后分别求出的值，从而可以判断原点在什么位置，本题得以解决。
本题考查数轴，解题的关键是明确数轴的特点，利用数形结合的思想解答问题。6.【答案】 【解析】【试题解析】
解：
解得，
方程与方程的解相同，

解得，
故选：．
解方程，求出，根据同解方程的定义将代入中计算即可．
本题考查的是同解方程，掌握一元一次方程的解法是解题的关键．7.【答案】 【解析】解：根据题意得，，
解得，
则．
故选A．
根据同类项是字母相同且相同字母的指数也相同，可得，的值，根据代数式求值，可得答案．
本题考查了同类项的知识，解答本题的关键是掌握同类项中相同字母的指数相同的概念．8.【答案】 【解析】解：当在线段延长线上时，如图，
、分别为、的中点，
，；
．
当在上时，如图，
同理可知，，
；
所以或，
故选：．
根据题意画出图形，再根据图形求解即可．
本题考查线段中点的定义，比较简单，注意有两种可能的情况；解答这类题目，应考虑周全，避免漏掉其中一种情况．9.【答案】 【解析】解：设多边形边数为，
过某个多边形一个顶点的所有对角线，把这个多边形分成个三角形，
，
解得：．
故选：．
根据过某个多边形一个顶点画对角线，把多边形分成个三角形，再结合题意可得，再解即可．
此题主要考查了多边形的对角线，关键是掌握过某个多边形一个顶点画对角线，把多边形分成个三角形．10.【答案】 【解析】【分析】
本题考查根据实际问题抽象出一元一次方程，得到乙的羊数的关系式是解决本题的关键．
根据甲的话可得乙羊数的关系式，根据乙的话得到等量关系即可列方程．
【解答】
解：因为甲对乙说：“把你的羊给我只，我的羊数就是你的羊数的两倍”，设甲有只羊，
所以乙有只，
因为乙回答说：“最好还是把你的羊给我只，我们的羊数就一样了”，
所以，即
故选C．11.【答案】 【解析】解：根据题意得：，
解得：．
故答案是：．
根据同类项的定义所含字母相同，相同字母的指数相同，即可求解．
考查了同类项，同类项定义中的两个“相同”：相同字母的指数相同，是易混点，因此成了中考的常考点．12.【答案】 【解析】解：根据题意得，，，
解得，，
所以，．
故答案为：．
根据非负数的性质列式求出、的值，然后代入代数式进行计算即可得解．
本题考查了非负数的性质：几个非负数的和为时，这几个非负数都为．13.【答案】 【解析】解：将代入得：．
解得；．
故答案为；．
将代入方程，得到关于的方程，接下来，解得的值即可．
本题主要考查的是一元一次方程的解得定义和解一元一次方程，掌握方程的解得定义是解题的关键．14.【答案】 【解析】解：由题意得：
与是相对面，与是相对面，与是相对面，
各相对面上所填的数字互为倒数，
，，，
的值，
故答案为：．
根据正方体的表面展开图找相对面的方法：一线隔一个，“”字两端是对面，可得与是相对面，与是相对面，与是相对面，然后根据倒数的意义可得，，，最后代入式子中进行计算即可解答．
本题考查了正方体相对两个面上的文字，倒数，熟练掌握正方体相对两个面上的文字是解题的关键．15.【答案】 【解析】解：当时，
，
则，
当时，
，
故答案为：．
将代入后得原式，然后将代入原式整理后代入数值计算即可．
本题考查代数式求值，结合已知条件求得是解题的关键．16.【答案】 【解析】解：由题意可得，
，
，
，
，
，
，
，
故答案为：．
根据题意，可以写出这列数的前几个数，从而可以发现数字的变化特点，从而可以得到的值．
本题考查数字的变化类，解答本题的关键是明确题意，发现数字的变化特点，写出相应项的值．17.【答案】解：去括号得：，
移项合并同类项得：，
系数化为，解得：；
去分母得：，
去括号得
移项合并同类项得：，
系数化为，解得：． 【解析】此题考查了解一元一次方程，熟练掌握运算法则是解本题的关键．
方程去括号，移项合并同类项，把系数化为，即可求出解；
方程去分母，去括号，移项合并同类项，把系数化为，即可求出解．18.【答案】解：


；





． 【解析】先乘除，后算加减，即可解答；
先算乘方，再算乘法，后算加减，有括号先算括号里，即可解答．
本题考查了有理数的混合运算，准确熟练地进行计算是解题的关键．19.【答案】原式，
当，时，原式． 【解析】原式去括号合并得到最简结果，把与的值代入计算即可求出值．
此题考查了整式的加减化简求值，熟练掌握运算法则是解本题的关键．20.【答案】 【解析】解：图中有个小正方体，
故答案为：；

如图所示：

找到所有正方体的个数，让它们相加即可；
主视图有列，每列小正方形数目分别为，，，；左视图有列，每列小正方形数目分别为，；俯视图有列，每列小正方形数目分别为，，，．
本题考查了作三视图，主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形．21.【答案】解：总人数是：，
则级的人数是：．
条形统计图补充如下：
；

级的学生人数占全班学生人数的百分比是：；
级所在的扇形的圆心角度数是；

级所占的百分比为，
级的人数为：人． 【解析】根据等人数为人，占扇形图的，求出总人数，可以得出的人数，即可画出条形统计图；
根据的人数即可得出所占百分比，进而得出所在的扇形的圆心角度数；
利用总体人数与组所占比例即可得出级学生人数．
此题主要考查了条形图的应用以及用样本估计总体和扇形图统计图的应用，利用图形获取正确信息以及扇形图与条形图相结合是解决问题的关键．22.【答案】解：点，分别是，的中点，，，
，，
；
点，分别是，的中点，
，，
． 【解析】根据线段中点的性质，可得、的长，根据线段的和差，可得答案；
根据线段中点的性质，可得、的长，根据线段的和差，可得答案．
本题考查了两点间的距离：连接两点间的线段的长度叫两点间的距离．23.【答案】解：设再经过后，点、相距，
、未相遇前相距，依题意可列
，解得，，
、相遇后相距，依题意可列
，解得，，
答：经过或后，点、相距．

点，只能在直线上相遇，则点旋转到直线上的时间为
或                                  
设点的速度为，
当秒时相遇，依题意得，，解得
当秒时相遇，依题意得，，解得
答：点的速度为或． 【解析】设经过，、两点相距，分相遇前和相遇后两种情况建立方程求出其解即可；
由于点，只能在直线上相遇，而点旋转到直线上的时间分两种情况，所以根据题意列出方程分别求解．
此题考查的知识点是一元一次方程的应用，关键是熟练掌握速度、路程、时间的关系．24.【答案】解：设第一次购进甲种商品件，则购进乙种商品件，
根据题意得：，
解得，
所以．
答：该超市第一次购进甲种商品件、乙种商品件；
由得，
则


元．
答：该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得利润元；
设第二次乙种商品是按原售价打折销售，
根据题意得：，
解得．
答：第二次乙商品是按原售价打折销售． 【解析】设第一次购进甲种商品件，则购进乙种商品件，根据总价单价数量，即可得出关于的一元一次方程，解之即可得出结论；
利用总利润每件的销售利润销售数量，即可求出结论；
设第二次乙种商品是按原价打折销售，利用总利润每件的销售利润销售数量，结合第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多元，即可得出关于的一元一次方程，解之即可得出结论．
本题考查了一元一次方程的知识，掌握一元一次方程的解法是关键．25.【答案】 【解析】解：第一次可得个正方形，第二次可得个正方形，第三次可得个正方形，
第次可得个正方形，
第次可得正方形：个；
故答案为：；
根据题意得：，
解得：；
第次划分后能有个正方形；
不能，
，
得：，
不是整数，
不能将正方形划分成有个正方形的图形；
由题意：

．
探究规律，利用规律即可解决问题；
构建方程即可解决问题；
构建方程即可判断；
利用数形结合的思想解决问题，根据计算即可．
本题考查了图形的变化类问题，掌握从特殊到一般的探究规律方法是关键．