2024年高考数学第一轮复习全程考评特训点点练 13

点点练13__三角函数的图象

1．为了得到函数y＝sin 的图象，只需把函数y＝sin 2x的图象(　　)

A．向左平移个单位长度

B．向右平移个单位长度

C．向左平移个单位长度

D．向右平移个单位长度

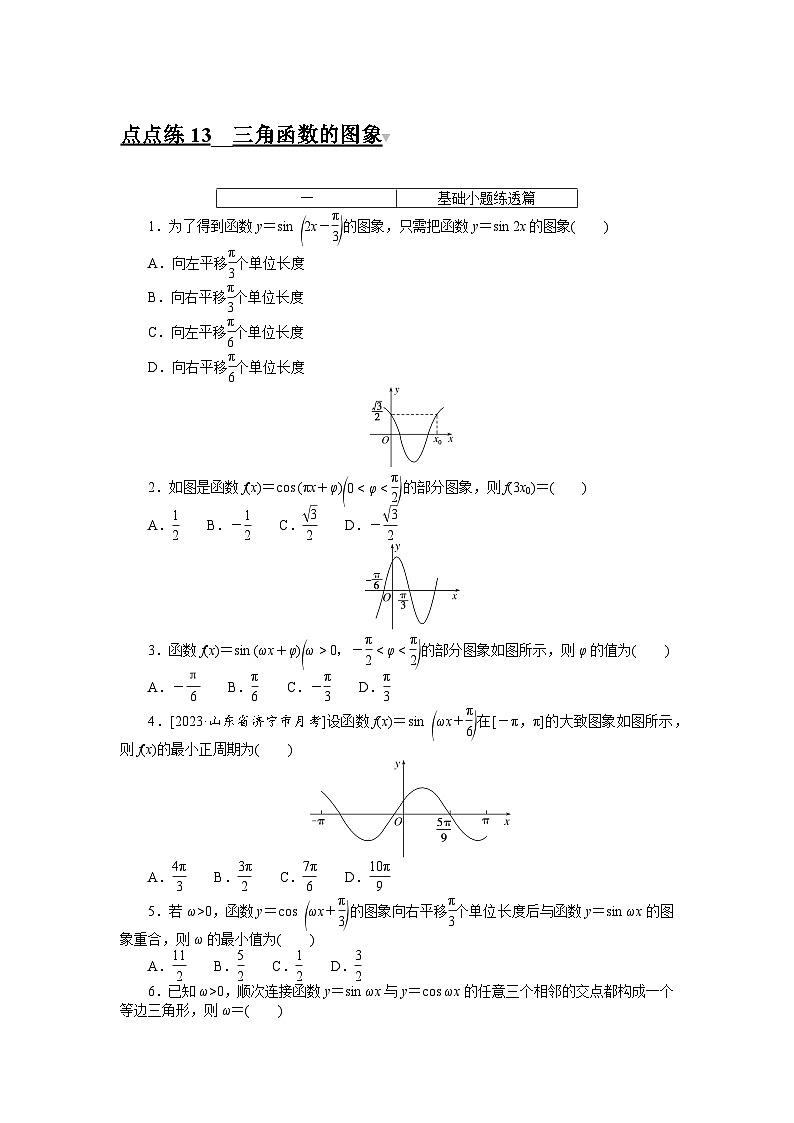
2．如图是函数f(x)＝cos (πx＋φ)的部分图象，则f(3x0)＝(　　)

A．    B．－    C．    D．－

3．函数f(x)＝sin (ωx＋φ)的部分图象如图所示，则φ的值为(　　)

A．－    B．    C．－    D．

4．[2023·山东省济宁市月考]设函数f(x)＝sin 在[－π，π]的大致图象如图所示，则f(x)的最小正周期为(　　)

A．    B．    C．    D．

5．若ω>0，函数y＝cos 的图象向右平移个单位长度后与函数y＝sin ωx的图象重合，则ω的最小值为(　　)

A．    B．    C．    D．

6．已知ω>0，顺次连接函数y＝sin ωx与y＝cos ωx的任意三个相邻的交点都构成一个等边三角形，则ω＝(　　)

A．π    B．    C．    D．π

7．[2023·上海市实验学校高三试题]已知函数f(x)＝A sin (ωx＋φ)(ω>0，0<φ<)的部分图象如图所示，则函数f(x)的解析式为________________．

8．已知函数f(x)＝3sin (ω>0)和g(x)＝3cos (2x＋φ)的图象的对称中心完全相同，若x∈，则f(x)的取值范围是________．

1.[2023·贵阳市联考]将函数f(x)＝sin (2x－)的图象向左平移a(a>0)个单位长度得到函数g(x)＝cos  2x的图象，则a的最小值为(　　)

A．    B．    C．    D．π

2．[2023·天津市南开区高三质量监测]已知函数f(x)＝A sin (ωx＋φ)(A>0，ω>0，|φ|<)的部分图象如图所示，则(　　)

A．f(x)＝2sin

B．f(x)＝2sin

C．f(x)＝2sin

D．f(x)＝2sin

3．[2023·四川省南充市适应性考试]将函数f(x)＝2sin (ω>0)的图象向右平移个单位，得到函数y＝g(x)的图象，若y＝g(x)在上为增函数，则ω的取值范围是(　　)

A．    B．

C．    D．

4．函数f(x)＝A sin (ωx＋φ)(A>0，ω>0，|φ|<)的部分图象如图所示，B，C分别为函数f(x)的图象与x轴、y轴的交点，|BC|＝.若函数f(x)的图象与直线y＝在(0，3)内的两个交点的坐标分别为(x1，y1)和(x2，y2)，则f(x1＋x2)＝ (　　)

A．－1    B．－    C．－    D．－2

5．[2023·四川省内江市第六中学月考]已知函数f(x)＝sin  (ω>0)，若f(x)在上恰有两个零点，且在上单调递增，则ω的取值范围是__________．

6.

[2023·江西省重点中学联考]函数f(x)＝2sin (ωx＋φ)(ω>0，0<φ<)的部分图象如图所示，该图象与y轴相交于点F(0，1)，与x轴相交于点B，C，点M为图象最高点，且三角形MBC的面积为π，则y＝f(x)图象的一个对称中心是________．(写出一个符合题意的即可)

1.[2020·全国卷Ⅰ]设函数f(x)＝cos (ωx＋)在[－π，π]的图象大致如图，则f(x)的最小正周期为(　　)

A．    B．    C．    D．

2．[2022·全国甲卷]设函数f(x)＝sin (ωx＋)在区间(0，π)恰有三个极值点、两个零点，则ω的取值范围是(　　)

A．    B．

C．    D．

3．[2021·全国乙卷]把函数y＝f(x)图象上所有点的横坐标缩短到原来的倍，纵坐标不变，再把所得曲线向右平移个单位长度，得到函数y＝sin 的图象，则f(x)＝(　　)

A．sin     B. sin

C. sin     D. sin

4．[2022·全国甲卷]将函数f(x)＝sin (ωx＋)(ω>0)的图象向左平移个单位长度后得到曲线C，若C关于y轴对称，则ω的最小值是(　　)

A．    B．    C．    D．

5．[2021·全国甲卷]已知函数f(x)＝2cos (ωx＋φ)的部分图象如图所示，则f＝________．

6．[2020·江苏卷]将函数y＝3sin 的图象向右平移个单位长度，则平移后的图象中与y轴最近的对称轴的方程是________________________________________________________________________．

1.某同学用“五点法”画函数f(x)＝A sin (ωx＋φ)在某一个周期内的图象时，列表并填入了部分数据，如下表：

(1)请将上表数据补充完整，并直接写出函数f(x)的解析式；

(2)将y＝f(x)图象上所有点向左平行移动θ(θ>0)个单位长度，得到y＝g(x)的图象．若y＝g(x)图象的一个对称中心为，求θ的最小值．

2．已知函数f(x)＝A sin (ωx＋φ)(A>0，ω>0，|φ|<)的部分图象如图所示．

(1)求函数f(x)的解析式；

(2)将函数y＝f(x)的图象上各点的纵坐标保持不变，横坐标缩短到原来的倍，再把所得的函数图象向左平移个单位长度，得到函数y＝g(x)的图象，求函数g(x)在区间上的最小值．