四川省成都市武侯区成都西川中学2023-2024学年九年级上学期9月月考数学试题(无答案)

这是一份四川省成都市武侯区成都西川中学2023-2024学年九年级上学期9月月考数学试题(无答案)，共6页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
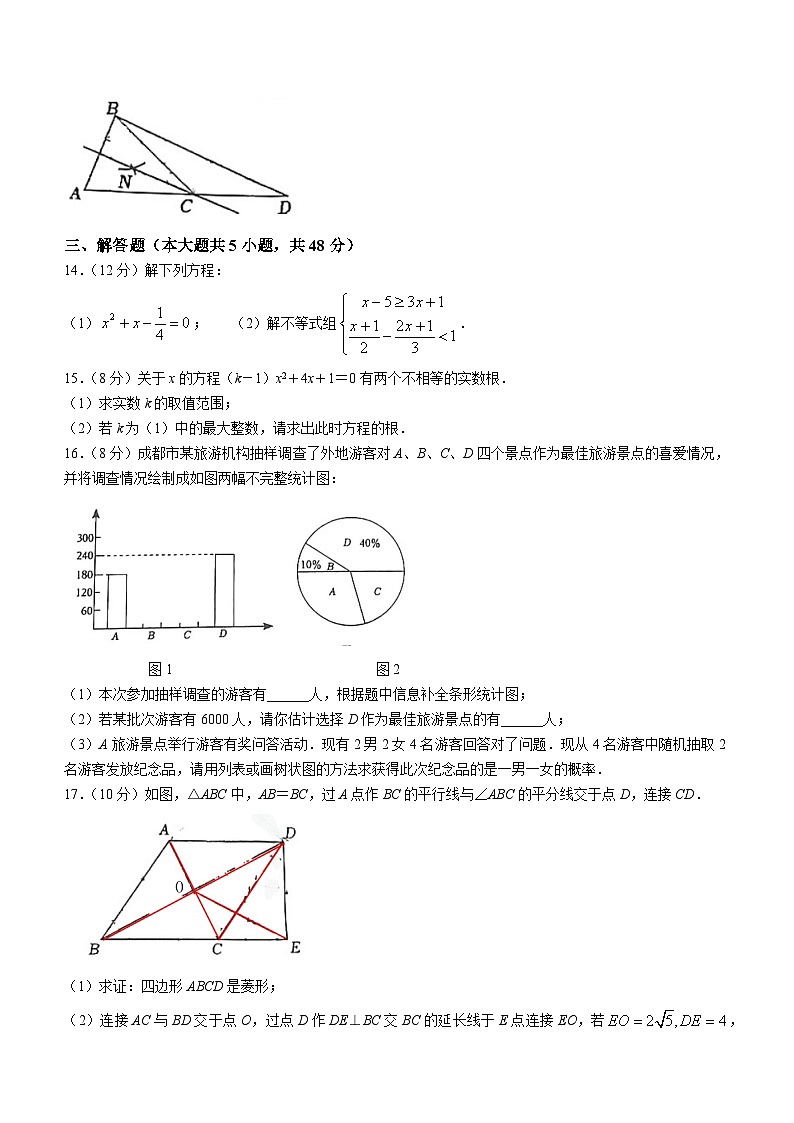
成都西川中学2023－2024学年9月九年级（上）数学练习班级______姓名______学号______A卷（共100分）一、选择题（本大题共8小题，每小题4分，共32分）1．在下列方程中，是关于x的一元二次方程的是（    ）A．ax2＋bx＋c＝0 B． C．5x2－3＝0 D．x（x－1）2＝3＋x22．若a＞b，则下列不等式不一定成立的是（    ）A．am＜bm B．－2a＜－2b C．a－3＞b－3 D．3．若一个多边形的内角和为其外角和的4倍，则这个多边形的边数是（    ）A．7 B．8 C．9 D．104．一次函数y＝kx＋b（k≠0）的图象如图，则不等式kx＋b＞3的解集为（    ）A．x＜－2.5 B．x＞－2.5 C．x＞2 D．x＜25．已知2是关于x的方程x2－2mx＋3m＝0的一个根，并且这个方程的两个根恰好是等腰△ABC的两条边长，则△ABC的周长为（    ）A．10 B．14 C．10或14 D．8或106．某公司今年4月的营业额为2500万元，按计划第二季度的总营业额要达到9100万元，设该公司5、6两月的营业额的月平均增长率为x．根据题意列方程，则下列方程正确的是（    ）A．2500（1＋x）2＝910 0 B．2500（1＋x%）2＝9100C．2500（1＋x）＋2500（1＋x）2＝9100 D．2500＋2500（1＋x）＋2500（1＋x）2＝91007．如图，已知△ABC，AB＝AC，将△ABC沿边BC翻转，得到的△DBC与原△ABC拼成四边形ABDC，则能直接判定四边形ABDC是菱形的依据是（    ）A．一组邻边相等的平行四边形是菱形 B．对角线互相垂直的平行四边形是菱形C．四条边相等的四边形是菱形 D．对角线互相平分的平行四边形是菱形8．如图，矩形ABCD中，连接AC，延长BC至点E，使BE＝AC，连接DE．若∠E＝75°，则∠BAC的度数是（    ）A．45° B．50° C.55° D．60°二、填空题（本大题共5小题，每小题4分，共20分）9．分解因式：ma2－6ma＋9m＝______．10．若分式，______．11．若一元二次方程x2－kx－1＝0的两根互为相反数，则k的值为______．12．如图，将两张长为8，宽为2的矩形纸条交叉，使重叠部分是一个菱形，容易知道当两张纸条垂直时，菱形的周长有最小值8，那么菱形周长的最大值是______．13．如图，分别以线段AB的两个端点A，B为圆心，大于为半径作弧，两弧交于点M，N，作直线MN，点C为直线MN上一点，连接CB，CA，以C为圆心，CB长为半径作弧，交AC的延长线于点D，连接BD．若∠BDC＝25°，则∠BAC的度数为______．三、解答题（本大题共5小题，共48分）14．（12分）解下列方程：（1）； （2）解不等式组．15．（8分）关于x的方程（k－1）x2＋4x＋1＝0有两个不相等的实数根．（1）求实数k的取值范围；（2）若k为（1）中的最大整数，请求出此时方程的根．16．（8分）成都市某旅游机构抽样调查了外地游客对A、B、C、D四个景点作为最佳旅游景点的喜爱情况，并将调查情况绘制成如图两幅不完整统计图：            图1                             图2（1）本次参加抽样调查的游客有______人，根据题中信息补全条形统计图；（2）若某批次游客有6000人，请你估计选择D作为最佳旅游景点的有______人；（3）A旅游景点举行游客有奖问答活动．现有2男2女4名游客回答对了问题．现从4名游客中随机抽取2名游客发放纪念品，请用列表或画树状图的方法求获得此次纪念品的是一男一女的概率．17．（10分）如图，△ABC中，AB＝BC，过A点作BC的平行线与∠ABC的平分线交于点D，连接CD．（1）求证：四边形ABCD是菱形；（2）连接AC与BD交于点O，过点D作DE⊥BC交BC的延长线于E点连接EO，若，求CE的长．18．（10分）正方形ABCD和正方形AEFG的边长分别为6和2，将正方形AEFG绕点A逆时针旋转．         图1                        图2                    图3（1）当旋转至图1位置时，连接BE，DG，线段BE和DG有何关系？请说明理由；（2）在图1中，连接BD，BF，DF，请直接写出在旋转过程中△BDF的面积最大值；（3）在旋转过程中，当点G，E，D在同一直线上时，请求出线段BE的长．B卷（共50分）一、填空题．（本大题共5小题，每小题4分，共20分）19．已知a是方程x2＋3x－1＝0的一个实数根，则2a2＋6a＋2021的值为______．20．已知关于x的方程x2＋（2k－1）x＋k2－1＝0有两个实数根x1，x2，若x1，x2满足x1x2＋x1＋x2＝3，求k的值为______．21．如图，在△ABC中，分别以AB，AC为边向外作正方形ABED和正方形ACGF．若点E，A，G在同一直线上，，则△ABC的面积为______．22．如图，在△ABC中，AB＝6，AC＝8，BC＝10，P为边BC上一动点（且点P不与点B，C重合），PE⊥AB于E，PF⊥AC于F，M为EF的中点．求EM的最小值______．23．对任意正整数n，若n为偶数则除以2，若n为奇数则乘3再加1，在这样一次变化下，我们得到一个新的自然数，在1937年LotharCollatz提出了一个问题：如此反复这种变换，是否对于所有的正整数，最终都能变换到1呢？这就是数学中著名的“考拉兹猜想”．如果某个正整数通过上述变换能变成1，我们就把第一次变成1时所经过的变换次数称为它的路径长，例如5经过5次变成1，则路径长m＝5．若输入数n，变换次数m，当m＝8时，n的所有可能值有______个，其中最小值为______．二、解答题（本大题共3小题，共30分）24．（8分）某商店经销一种销售成本为每千克40元的水产品，据市场分析，若每千克50元销售，一个月能售出500kg，销售单价每涨2元，月销售量就减少20kg，针对这种水产品情况，请解答以下问题：（1）当销售单价定为每千克55元时，计算销售量和月销售利润．（2）商店想在月销售成本不超过10000元的情况下，使得月销售利润达到8000元，销售单价应为多少？25．（10分）如图，在平面直角坐标系中，直线分别交x轴，y轴于点C、点B，点A在x轴的负半轴上，满足，直线l∶y＝－3x＋b经过点C，连接AB．                                        备用图（1）求直线AB的解析式及b的值；（2）在直线l上存在一点P，使得，求点P的坐标；（3）若点M是直线l上一动点，且点M在x轴的上方，点N是平面内任意一点，是否存在点M、N，使以点B，C，M，N为顶点的四边形是菱形．若存在，请直接写出满足条件的点M的坐标，若不存在，请说明理由．26．（12分）数学活动课上，老师给出如下定义：如果一个矩形的其中一边是另一边的2倍，那么称这个矩形为“和谐矩形”．如图1，在矩形ABCD中，AD＝2AB，则矩形ABCD是“和谐矩形”．E是AD边上任意一点，连接BE，作BE的垂直平分线分别交AD，BC于点F，G，FG与BE的交点为O，连接BF和EG．        图1                    图2                 图3（1）试判断四边形BFEG的形状，并说明理由；（2）如图2，在“和谐矩形”ABCD中，若AB＝2，且AB＜AD，E是边AD上一个动点，把△ABE沿BE折叠．点A落在点．处，若恰在矩形的对称轴上，则AE的长为______（直接写出答案）；（3）如图3，记四边形BFEG的面积为S1，“和谐矩形”ABCD的面积为S2，且，若AB＝a（a为常数），且AB＜AD，求FG的长．（用含有a的代数式表示）．