2024年数学高考大一轮复习第四章 §4.5　三角函数的图象与性质（附答单独案解析）

§4.5　三角函数的图象与性质

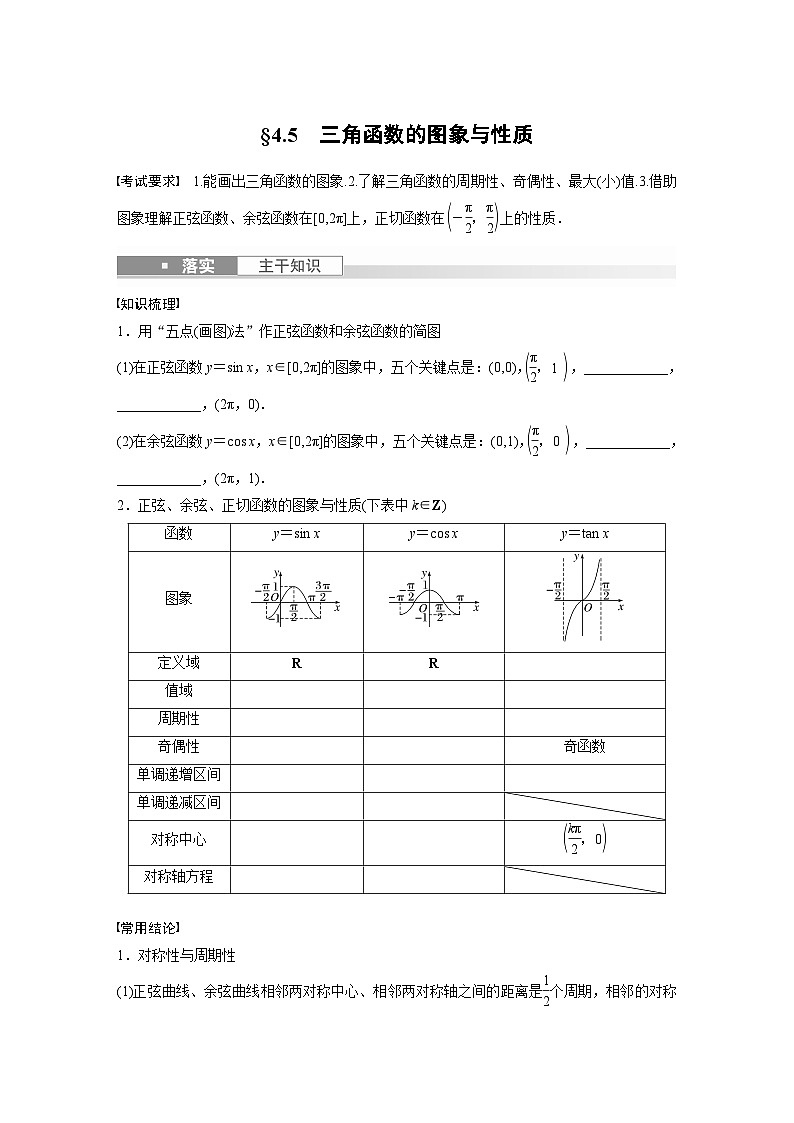
考试要求　1.能画出三角函数的图象.2.了解三角函数的周期性、奇偶性、最大(小)值.3.借助图象理解正弦函数、余弦函数在[0,2π]上，正切函数在上的性质．

知识梳理

1．用“五点(画图)法”作正弦函数和余弦函数的简图

(1)在正弦函数y＝sin x，x∈[0,2π]的图象中，五个关键点是：(0,0)，，____________，____________，(2π，0)．

(2)在余弦函数y＝cos x，x∈[0,2π]的图象中，五个关键点是：(0,1)，，____________，____________，(2π，1)．

2．正弦、余弦、正切函数的图象与性质(下表中k∈Z)

常用结论

1．对称性与周期性

(1)正弦曲线、余弦曲线相邻两对称中心、相邻两对称轴之间的距离是个周期，相邻的对称中心与对称轴之间的距离是个周期．

(2)正切曲线相邻两对称中心之间的距离是个周期．

2．奇偶性

若f(x)＝Asin(ωx＋φ)(A，ω≠0)，则

(1)f(x)为偶函数的充要条件是φ＝＋kπ(k∈Z)．

(2)f(x)为奇函数的充要条件是φ＝kπ(k∈Z)．

思考辨析

判断下列结论是否正确(请在括号中打“√”或“×”)

(1)y＝cos x在第一、二象限内单调递减．(　　)

(2)若非零常数T是函数f(x)的周期，则kT(k是非零整数)也是函数f(x)的周期．(　　)

(3)函数y＝sin x图象的对称轴方程为x＝2kπ＋(k∈Z)．(　　)

(4)函数y＝tan x在整个定义域上是增函数．(　　)

教材改编题

1．若函数y＝2sin 2x－1的最小正周期为T，最大值为A，则(　　)

A．T＝π，A＝1   B．T＝2π，A＝1

C．T＝π，A＝2   D．T＝2π，A＝2

2．函数y＝－tan的单调递减区间为________________．

3．函数y＝3－2cos的最大值为______，此时x＝__________.

题型一　三角函数的定义域和值域

例1 (1)函数y＝的定义域为(　　)

A.

B.(k∈Z)

C.(k∈Z)

D．R

听课记录：______________________________________________________________

________________________________________________________________________

(2)函数f(x)＝sin－3cos x的最小值为________．

听课记录：______________________________________________________________

________________________________________________________________________

(3)函数y＝sin x－cos x＋sin xcos x的值域为________．

听课记录：______________________________________________________________

________________________________________________________________________

思维升华 三角函数值域的不同求法

(1)把所给的三角函数式变换成y＝Asin(ωx＋φ)的形式求值域．

(2)把sin x或cos x看作一个整体，转换成二次函数求值域．

(3)利用sin x±cos x和sin xcos x的关系转换成二次函数求值域．

跟踪训练1 (1)(2021·北京)函数f(x)＝cos x－cos 2x，试判断函数的奇偶性及最大值(　　)

A．奇函数，最大值为2

B．偶函数，最大值为2

C．奇函数，最大值为

D．偶函数，最大值为

(2)函数y＝lg sin x＋的定义域为________________．

题型二　三角函数的周期性与对称性

例2 (1)设函数f(x)＝2sin＋，则下列叙述正确的是(　　)

A．f(x)的最小正周期为2π

B．f(x)的图象关于直线x＝对称

C．f(x)在上的最小值为－

D．f(x)的图象关于点对称

听课记录：______________________________________________________________

________________________________________________________________________

(2)函数f(x)＝3sin＋1，φ∈(0，π)，且f(x)为偶函数，则φ＝________，f(x)图象的对称中心为________________．

听课记录：______________________________________________________________

________________________________________________________________________

思维升华 (1)奇偶性的判断方法：三角函数中奇函数一般可化为y＝Asin ωx或y＝Atan ωx的形式，而偶函数一般可化为y＝Acos ωx的形式．

(2)周期的计算方法：利用函数y＝Asin(ωx＋φ)，y＝Acos(ωx＋φ)(ω>0)的周期为，函数y＝Atan(ωx＋φ)(ω>0)的周期为求解．

跟踪训练2 (1)(2021·全国乙卷)函数f(x)＝sin ＋cos 最小正周期和最大值分别是(　　)

A．3π和   B．3π和2

C．6π和   D．6π和2

(2)(2020·全国Ⅲ)已知函数f(x)＝sin x＋，则(　　)

A．f(x)的最小值为2

B．f(x)的图象关于y轴对称

C．f(x)的图象关于直线x＝π对称

D．f(x)的图象关于直线x＝对称

题型三　三角函数的单调性

命题点1　求三角函数的单调区间

例3 函数f(x)＝sin的单调递减区间为________________________．

听课记录：______________________________________________________________

________________________________________________________________________

延伸探究 若函数不变，求在[0，π]上的单调递减区间．

________________________________________________________________________

________________________________________________________________________

________________________________________________________________________

________________________________________________________________________

________________________________________________________________________

________________________________________________________________________

命题点2　根据单调性求参数

例4 (1)(2023·西宁模拟)若函数f(x)＝cos在区间[－a，a]上单调递增，则实数a的最大值为(　　)

A.  B.   C.   D. π

听课记录：______________________________________________________________

________________________________________________________________________

(2)已知ω>0，函数f(x)＝sin在上单调递减，则ω的取值范围是________．

听课记录：______________________________________________________________

________________________________________________________________________

思维升华 (1)已知三角函数解析式求单调区间

求形如y＝Asin(ωx＋φ)或y＝Acos(ωx＋φ)(其中ω>0)的单调区间时，要视“ωx＋φ”为一个整体，通过解不等式求解．但如果ω<0，可先借助诱导公式将ω化为正数，防止把单调性弄错．

(2)已知三角函数的单调区间求参数

先求出函数的单调区间，然后利用集合间的关系求解．

跟踪训练3 (1)(2022·北京)已知函数f(x)＝cos2x－sin2x，则(　　)

A．f(x)在上单调递减

B．f(x)在上单调递增

C．f(x)在上单调递减

D．f(x)在上单调递增

(2)已知函数f(x)＝sin(ω>0)，则“函数f(x)在上单调递增”是“0<ω<2”的(　　)

A．充分不必要条件

B．必要不充分条件

C．充要条件

D．既不充分也不必要条件