湖南省部分校教育联盟2022-2023学年高三上学期入学摸底测试数学试题

这是一份湖南省部分校教育联盟2022-2023学年高三上学期入学摸底测试数学试题，共20页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
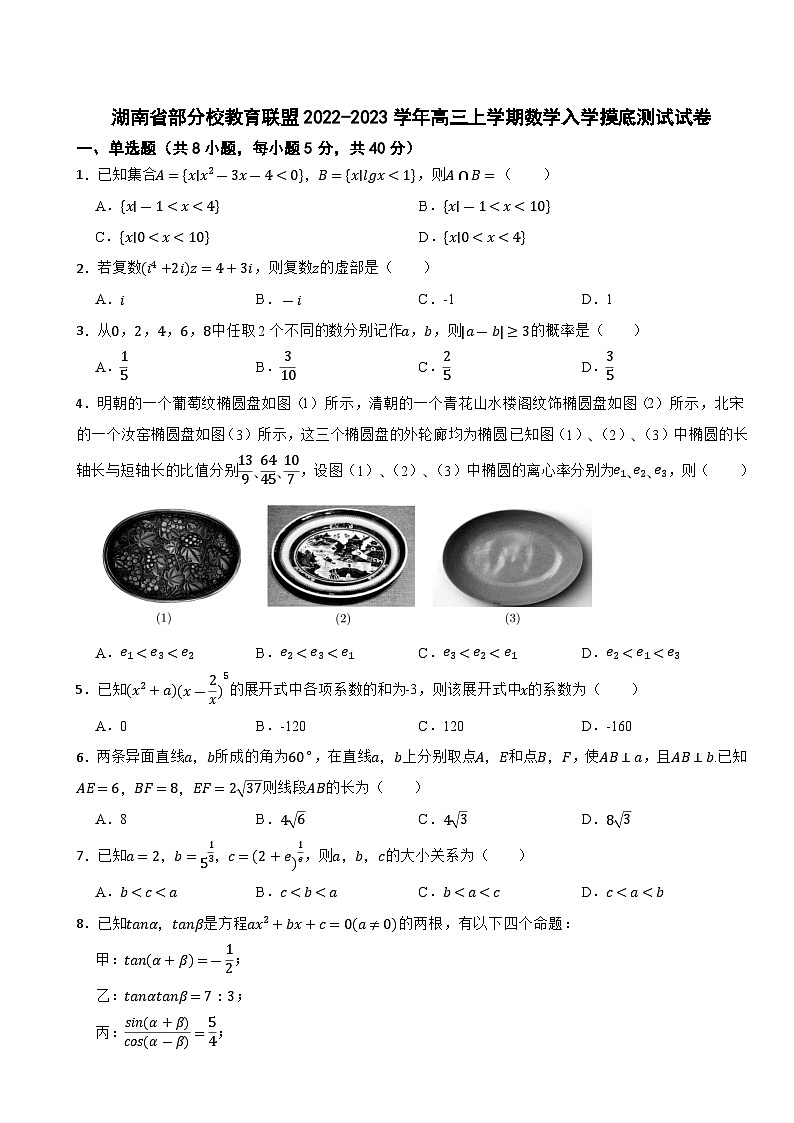
 湖南省部分校教育联盟2022-2023学年高三上学期数学入学摸底测试试卷一、单选题（共8小题，每小题5分，共40分）1．已知集合，则（　　）A． B．C． D．2．若复数，则复数的虚部是（　　）A． B． C．-1 D．13．从，，，，中任取2个不同的数分别记作，，则的概率是（　　）A． B． C． D．4．明朝的一个葡萄纹椭圆盘如图（1）所示，清朝的一个青花山水楼阁纹饰椭圆盘如图（2）所示，北宋的一个汝窑椭圆盘如图（3）所示，这三个椭圆盘的外轮廊均为椭圆.已知图（1）､（2）､（3）中椭圆的长轴长与短轴长的比值分别，设图（1）､（2）､（3）中椭圆的离心率分别为，则（　　）A． B． C． D．5．已知的展开式中各项系数的和为-3，则该展开式中的系数为（　　）A．0 B．-120 C．120 D．-1606．两条异面直线所成的角为，在直线上分别取点和点，使，且.已知则线段的长为（　　）A．8 B． C． D．7．已知，则的大小关系为（　　）A． B． C． D．8．已知是方程的两根，有以下四个命题：甲：；乙：；丙：；丁：.如果其中只有一个假命题，则该命题是（　　）A．甲 B．乙 C．丙 D．丁二、多选题（共4小题，每小题5分，共20分）9．下列命题正确的是（　　）A．若甲､乙两组数据的相关系数分别为0.66和-0.85，则乙组数据的线性相关性更强B．已知样本数据的方差为4，则的标准差是4C．在检验与是否有关的过程中，根据所得数据算得，已知，则有的把握认为和有关D．对具有线性相关关系的变量，有一组观测数据，其线性回归方程是，且，则实数的值是10．若函数在区间上的最大值为6，则下列结论正确的是（　　）A．B．是函数的一个周期C．当时，不等式恒成立，则实数的取值范围是D．将函数的图像向左移动个单位得到函数的图像，则函数是一个偶函数11．树人中学的“希望工程”中，甲､乙两个募捐小组暑假期间走上街头分别进行了为期两周的募捐活动.两个小组第1天都募得1000元，之后甲小组继续按第1天的方法进行募捐，则从第2天起，甲小组每一天得到的捐款都比前一天少50元；乙小组采取了积极措施，从第1天募得的1000元中拿出了600元印刷宣传材料，则从第2天起，第天募得的捐款数为元.若甲小组前天募得捐款数累计为元，乙小组前天募得捐款数累计为元（需扣除印刷宣传材料的费用），则（　　）A．B．甲小组募得捐款为9550元C．从第7天起，总有D．且12．在直角坐标系中，抛物线与直线交于两点，且.抛物线的准线与轴交于点是以为圆心，为半径的圆上的一点（非原点），过点作抛物线的两条切线，切点分别为.则（　　）A． B．直线的方程为C． D．面积的最大值是三、填空题（共4小题，每小题5分，共20分）13．函数的极大值点是　     　.14．已知抛物线的焦点在轴上，直线与抛物线交于点，且.写出抛物线的一个标准方程　                                                    　.15．定义在上的奇函数，当时，，则曲线上的点到直线y=-x+1的最小距离为　     　.16．三棱锥中，，底面是边长为2的正三角形，分别是的中点，且，若为三棱锥外接球上的动点，则点到平面距离的最大值为　     　.四、解答题（共6题，共70分）17．已知锐角中，角所对的边分别为.（1）求；（2）若，求的取值范围.18．如图，在三棱柱中，平面平面，四边形是菱形，是的中点.（1）证明：平面；（2）求直线与平面所成角的正弦值.19．2022年2月20日，北京冬奥会在鸟巢落下帷幕，中国队创历史最佳战绩.北京冬奥会的成功举办推动了我国冰雪运动的普及，让越来越多的青少年爱上了冰雪运动.这场冰雪盛会是运动健儿奋力拼搏的舞台，也是中外文明交流互鉴的舞台，诠释着新时代中国的从容姿态，传递出中华儿女与世界人民“一起向未来”的共同心声.某学校统计了全校学生观看北京冬奥会开幕式和闭幕式的时长情况（单位：分钟），并根据样本数据绘制得到右下图所示的频率分布直方图.（1）求频率分布直方图中的值，并估计样本数据的90%分位数；（2）采用样本量比例分配的分层随机抽样方式，从观看时长在的学生中抽取9人.若从这9人中随机抽取3人在全校交流观看体会，设抽取的3人中观看时长在的人数为，求的分布列和数学期望.20．已知数列满足，且.（1）求数列的通项公式；（2）设，求证：.21．设是双曲线的左､右两个焦点，为坐标原点，若点在双曲线的右支上，且的面积为3.（1）求双曲线的渐近线方程；（2）若双曲线的两顶点分别为，过点的直线与双曲线交于，两点，试探究直线与直线的交点是否在某条定直线上？若在，请求出该定直线方程；若不在，请说明理由.22．已知函数，其中.（1）若直线是曲线的切线，求负数的值；（2）设.（i）讨论函数的单调性；（ii）若函数的导函数在区间上存在零点，证明：当时，.
答案解析部分1．【答案】D【知识点】交集及其运算【解析】【解答】由得，所以，又，所以，故答案为：D.
【分析】 先解一元二次不等式，对数不等式求出A、B，再利用交集运算求解出答案.2．【答案】C【知识点】复数代数形式的乘除运算【解析】【解答】由可得：复数复数的虚部是-1，故答案为：C.
【分析】 把已知等式变形，再由复数代数形式的乘除运算化简得答案.3．【答案】D【知识点】列举法计算基本事件数及事件发生的概率【解析】【解答】解：从0，2，4，6，8中任取2个不同的数，，共有个基本事件， 取出的2个数之差的绝对值等于有，，，共4个基本事件，所以所求概率为.故答案为：D
【分析】首先求出基本事件总数，再用列举法列出取出的2个数之差的绝对值等于2的事件数，最后利用对立事件和古典概型的概率公式计算可得答案.4．【答案】B【知识点】椭圆的简单性质【解析】【解答】因为椭圆的离心率，所以椭圆的长轴长与短轴长的比值越大，离心率越大.由，所以.故答案为：B.
【分析】根据离心率的定义可知，长轴长与短轴长的比值越大，离心率越大，根据三者的长轴长与短轴长的比值求出答案.5．【答案】A【知识点】二项式定理；二项式系数的性质【解析】【解答】因为的展开式中各项系数的和为-3，所以令，得，解得，∵的展开式为则展开式中含的项为，故的系数为0.故答案为：A．
【分析】 由题意，先求出a=2，再利用二项式展开式的通项公式，求出展开式中x的系数.6．【答案】B【知识点】向量的模【解析】【解答】由题意知：，所以，又异面直线所成的角为，则所以，则或（舍去）故答案为：B.
【分析】根据向量的线性运算可得，两边同时平方，利用向最的数量积运算，结合题意化简得到，进而求出答案.7．【答案】A【知识点】函数单调性的性质；利用导数研究函数的单调性【解析】【解答】由题意，可得，所以令，则，令，则，所以在上单调递减，，所以恒成立，所以在上单调递减，因为，所以，即，所以，所以，即.故答案为：A.
【分析】化简变形，由题意可得，构造，得到则，再令求得函数的单调性，结合单调性，即可求解出答案.8．【答案】B【知识点】一元二次方程的根与系数的关系；两角和与差的余弦公式；两角和与差的正弦公式；两角和与差的正切公式【解析】【解答】因为是方程的两根，所以，则甲：；丙：.若乙､丁都是真命题，则，所以，，两个假命题，与题意不符，所以乙､丁一真一假，假设丁是假命题，由丙和甲得，所以，即，所以，与乙不符，假设不成立；假设乙是假命题，由丙和甲得，又，所以，即与丙相符，假设成立；故假命题是乙，故答案为：．
【分析】根据韦达定理可得，对乙、丁运算分析可知乙、丁一真一假，分别假设乙、丁是假命题，逐项进行判断，可得答案.9．【答案】A,B【知识点】极差、方差与标准差；线性相关；线性回归方程；独立性检验的基本思想【解析】【解答】两个随机变量的线性相关性越强，相关系数的绝对值越接近于1，故正确；中样本数据的方差为4，则的方差为，标准差为4，B符合题意；C中由6.352，没有的把握判断认为和有关，C不正确；D中，由得，D不正确；故答案为：AB.
【分析】根据两个随机变量的线性相关性，即可判断A；根据方差与标准差，即可判断B；根据独立性检验，即可判断C；根据线性回归方程，即可判断D.10．【答案】B,D【知识点】三角函数中的恒等变换应用；正弦函数的性质；函数y=Asin（ωx+φ）的图象变换【解析】【解答】，当时，则，所以当时，的最大值为6，即，所以，A不正确；∵的最小正周期，则是函数的一个周期，B符合题意；当时，，所以不等式恒成立，则，解得，选项不正确；函数的图像向左移动个单位得到函数，函数是一个偶函数，选项正确.故答案为：BD．
【分析】将函数恒等变形化简，由在上的最大值为6，可得m的值，进而求出函数的解析式，进而逐一判断，可得答案.11．【答案】A,C【知识点】等差数列的通项公式；等差数列的前n项和【解析】【解答】由题可知且， 设代表第天甲小组募得捐款，且，对于甲小组，，所以，所以，所以且，所以，B不正确；设代表第天乙小组募得捐款，由题可知，，所以，，D不符合题意；因为，故该A符合题意；C，令，所以，而当时，，所以数列为递增数列，因此，所以，C符合题意.故答案为：AC
【分析】利用等差数列求和公式求出甲小组两周的募捐的钱数，判断B；利用等比数列求和公式及分组求和，得到乙小组两周募捐的钱数，判断D；计算S6， T6，比较大小，判断A；令，，判断C.12．【答案】B,C,D【知识点】直线与圆锥曲线的综合问题【解析】【解答】依题意可设，则，因为，所以，故.又，所以，故抛物线的方程为，所以选项不正确，；不妨设在第一象限，在第四象限，由可得，，所以直线的斜率为，则直线的方程为，化简为；同理求得的方程为，因为点在直线，上，所以 ，由此可知，的坐标都满足，由于两点确定一条直线，故可得直线AB的方程为，所以B选项正确；由A的分析可知抛物线的准线方程为，故，所以以为圆心，为半径的圆的方程为 ，由于为圆上动点（非原点），故，C符合题意；联立方程组，整理得， ，则，故，点到直线的距离，故的面积，由题可知，，则圆的方程为，故，因为，所以，所以，故面积的最大值为为，D符合题意；故答案为：BCD
【分析】利用向量的数量积等于0可求得p=2，判断A；确定抛物线方程，利用导数表示出抛物线切线方程，结合两点确定一条直线可得AB方程，判断B；求出以M为圆心，|OM |为半径的圆的方程，即可知，判断C；求出弦长AB，求出点到直线AB的距离，即可表示出△ABG面积，从而求得其最大值，判断D.13．【答案】【知识点】利用导数研究函数的单调性；利用导数研究函数的极值【解析】【解答】由题意，函数，可得，令，即，解得，当时，，故在上为单调递增函数，当时，，故在上为单调递减函数，所以函数的极大值点是.故答案为：.
【分析】求得函数的导数，利用导数的符号求得函数的单调性，结合极值点的概念，即可求解出的极大值点.14．【答案】或或或（写出一个即可）【知识点】抛物线的定义【解析】【解答】设所求焦点在轴上的抛物线的方程为，， 由抛物线定义得.又∵或，故所求抛物线方程为或.故答案为：或或或．（写出一个即可）
【分析】由已知可设抛物线的标准方程为，进而求出A点的坐标，结合抛物线的性质，求出满足条件的p值，可得答案.15．【答案】【知识点】平面内点到直线的距离公式【解析】【解答】由对称性可知，只需要比较与时的距离.设，因为函数是奇函数，所以，则设点，则，解得：此时点到直线y=-x+1的距离，设，则原点到直线y=-x+1的距离，因为，所以曲线上的点到直线y=-x+1的最小距离为.故答案为：．
【分析】先根据奇函数定义求时 的解析式，此时斜率为1的点到直线的距离最小，再与原点到直线的距离相比较，求出曲线上的点到直线y=-x+1的最小距离.16．【答案】【知识点】棱柱、棱锥、棱台的体积【解析】【解答】为边长为2的等边三角形，为正三棱锥，，又分别为中点，，，又平面平面，为正方体一部分，故，即，∵为三棱锥外接球上的动点，∴当位于正方体的如图所示的顶点处，点到平面距离最大，设为，∴可求得三棱锥的体积为：，∴，解得：故答案为：
【分析】先证得平面，再求得，从而得 为正方体一部分，进而知正方体的体对角线即为球直径，从而求解出点到平面距离的最大值 .17．【答案】（1）解：由及正弦定理得所以，又，因为，所以，所以.因为，所以（2）解：由正弦定理得，所以.因为是锐角三角形，所以，解得.因为在上单调递增，所以.从而，所以，即的取值范围是.【知识点】正弦定理【解析】【分析】(1)由题意，利用正弦定理、两角和的正弦公式，求得cosB的值，可得B的值；
(2)由题意，利用正弦定理，先求出a的表达式以及角C的范围，再利用正切函数的值域，求得 的取值范围.18．【答案】（1）证明：连接，因为四边形是菱形，则，因为，故为等边三角形，所以.因为平面平面，平面平面平面，所以平面，平面，所以.因为，所以.又，所以平面.（2）解：连接，因为是的中点，所以.又因为平面平面，平面平面平面，所以平面.设，因为，以点为坐标原点，所在直线分别为轴建立如图所示的空间直角坐标系，则，.设平面的法向量是，则，取，可得.设直线与平面所成角为所以，∴直线与平面所成角的正弦值是.【知识点】直线与平面垂直的判定；用空间向量研究直线与平面所成的角【解析】【分析】(1)根据题意利用面面垂直的性质定理可证得 平面，再结合线面垂直的判定定理证明出 平面；
(2) 以点为坐标原点，所在直线分别为轴建立如图所示的空间直角坐标系， 先求出平面的法向量，再根据 ， 计算可求出直线与平面所成角的正弦值.19．【答案】（1）解：由题意，，解得.由频率分布直方图知，观看时长在200分钟以下占比为.观看时长在240分钟以下占比为.所以90%分位数位于内，分位数为.（2）解：由题意，观看时长[200，240）､[240，280]对应的频率分别为0.16和0.08，所以采用分层随机抽样的方式在两个区间中应分别抽取6人和3人.于是抽取的3人中观看时长在中的人数X的所有可能取值为.所以，的分布列为0123P所以，.【知识点】频率分布直方图；离散型随机变量及其分布列；离散型随机变量的期望与方差【解析】【分析】 (1)先由频率和为1解得a，按百分位数的定义求出样本数据的90%分位数；
(2)利用分层随机抽样求出在两个区间中应分别抽取6人和3人，得到X的所有可能取值为0，1， 2， 3，分别求出对应的概率，写出分布列，求出 的分布列和数学期望.20．【答案】（1）解：由得，两式相除得，所以都是公比为2的等比数列，由及得，所以为奇数时，，为偶数时，，所以（2）证明：，则，两式相减得，所以，因为，所以单调递增所以成立，所以.【知识点】数列的求和；数列的递推公式【解析】【分析】(1)由 ，且 可得 ， ， 相除可得 ，可得数列 的奇数项与偶数项都成等比数列，通过分类讨论，利用等比数列的通项公式即可得出数列的通项公式；
(2) ，利用错位相减法即可得出Sn，结合数列的单调性即可证出结论 .21．【答案】（1）解：由得，且所以即解得又，故双曲线的渐近线方程为（2）解：由（1）可知双曲线的方程为.（i）当直线的斜率不存在时，，直线的方程为，直线的方程为，联立直线与直线的方程可得，（ii）当直线的斜率存在时，易得直线l不和渐近线平行，且斜率不为0，设直线的方程为，联立得直线的方程为，直线的方程为，联立直线与直线的方程可得：，两边平方得，又满足，.，，或，（舍去.综上，在定直线上，且定直线方程为.【知识点】双曲线的定义；双曲线的简单性质；直线与圆锥曲线的综合问题【解析】【分析】(1)由 ，得P在以F1F2为直径的圆上，则 ，由△PF1F2的面积，勾股定理及双曲线的定义列式求得a，再由隐含条件求解b，则求出双曲线的渐近线方程；
(2) （i）当直线的斜率不存在时，，求出直线与直线的方程，联立直线与直线的方程求出点Q的坐标，（ii）当直线的斜率存在时，易得直线l不和渐近线平行，且斜率不为0，设直线的方程为 由(1)求得双曲线方程为 ， 联立直线方程与双曲线方程，联立两直线方程，利用根与系数的关系求得Q点的横坐标为定值，即可得到直线与直线的交点在定直线上 .22．【答案】（1）解：因为，所以由直线是曲线的切线可知，即又，所以，则切点坐标为，所以故.（2）解：（i）.①若即的解为，所以当时，单调递减；当时，单调递增；②若即的解为或，所以当时，单调递增；当时，单调递减③若即恒成立，所以在上单调递增；④若即的解为或，所以当时，单调递增；当时，单调递减.综上所述：若，当时，单调递减，时，单调递增；若，当时，单调递增，时，单调递减；若在上单调递增；若，当时，单调递增，时，单调递减.（ii）证明：∵在区间上存在零点，设零点为，则，所以在上单调递减，在上单调递增故设，则，设，则在内单调递减，又，故在上恒成立，故在内单调递减，所以，故当时，.【知识点】利用导数研究函数的单调性；利用导数研究曲线上某点切线方程【解析】【分析】(1)利用导数的几何意义运算求解，可得负数的值；
(2) (i)根据题意整理可得 ，根据导数与单调性的关系分类讨论可得函数的单调性；
（ii）结合(i)分析可知 ，，构建新函数 ， 利用导数求F(x)min，即可得证.