

2022-2023学年福建省泉州市德化县多校联考七年级(下)期中数学试卷(含解析)
展开2022-2023学年福建省泉州市德化县多校联考七年级(下)期中数学试卷
一、选择题(本大题共10小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
1.若代数式的值为,则的值为( )
A. B. C. D.
2.已知方程组,将可得( )
A. B. C. D.
3.不等式的解集为( )
A. B. C. D.
4.下列各对数中,可以是二元一次方程的解的是( )
A. B. C. D.
5.我们知道,物体的体积、质量与它的密度的关系为,将等式去分母得,其变形的依据是( )
A. 等式的性质 B. 不等式的性质 C. 等式的性质 D. 不等式的性质
6.某货运公司用汽车运一批货物,第一次运走总数的,而第二次运走吨,还剩下吨,则这批货物共有( )
A. 吨 B. 吨 C. 吨 D. 吨
7.若,则下列不等式成立的是( )
A. B. C. D.
8.若关于的不等式的解集在数轴上表示如图所示,则关于的方程的解为( )
A. B. C. D.
9.中国古代数学著作孙子算经中有一段文字大意是:甲、乙两人各有若干钱,如果甲得到乙所有钱的一半,那么甲共有钱文;如果乙得到甲所有钱的,那么乙共有钱文,甲、乙两人原来各有多少钱?设甲、乙两人原来各有钱文,文,可列方程组为( )
A. B. C. D.
10.已知关于,的二元一次方程组下列结论错误的是( )
A. 当方程组的解,的值互为相反数时,
B. 当时,方程组的解也是方程的解
C. 若用表示,则
D. 无论取什么实数,的值始终不变
二、填空题(本大题共6小题,共24.0分)
11.若方程是关于,的二元一次方程,则 ______ .
12.如图,一架天平上放置质量分别为,的两个物体,试比较大小: ______ 填“”或“”
13.已知不等式的解集为,则的取值范围是______ .
14.已知是方程的解,则的值为______ .
15.“曹冲称象”如图是广泛流传的故事按照曹冲的方法,先将象牵到大船上并在船侧面标记水位,再将象牵出,然后往船上抬入块等重的条形石,并在船上留名搬运工每名搬运工的体重均为千克,这时水位恰好到达标记位置,如果再抬入块同样的条形石,船上只留名搬运工,水位也恰好到达标记位置,则象的体重为______ 吨参考数据:吨千克
16.若方程组的解是则关于,的方程组的解是______ .
三、解答题(本大题共9小题,共86.0分。解答应写出文字说明,证明过程或演算步骤)
17.本小题分
解方程:.
18.本小题分
若代数式的值不小于,求的取值范围.
19.本小题分
下面是老师布置的数学作业:
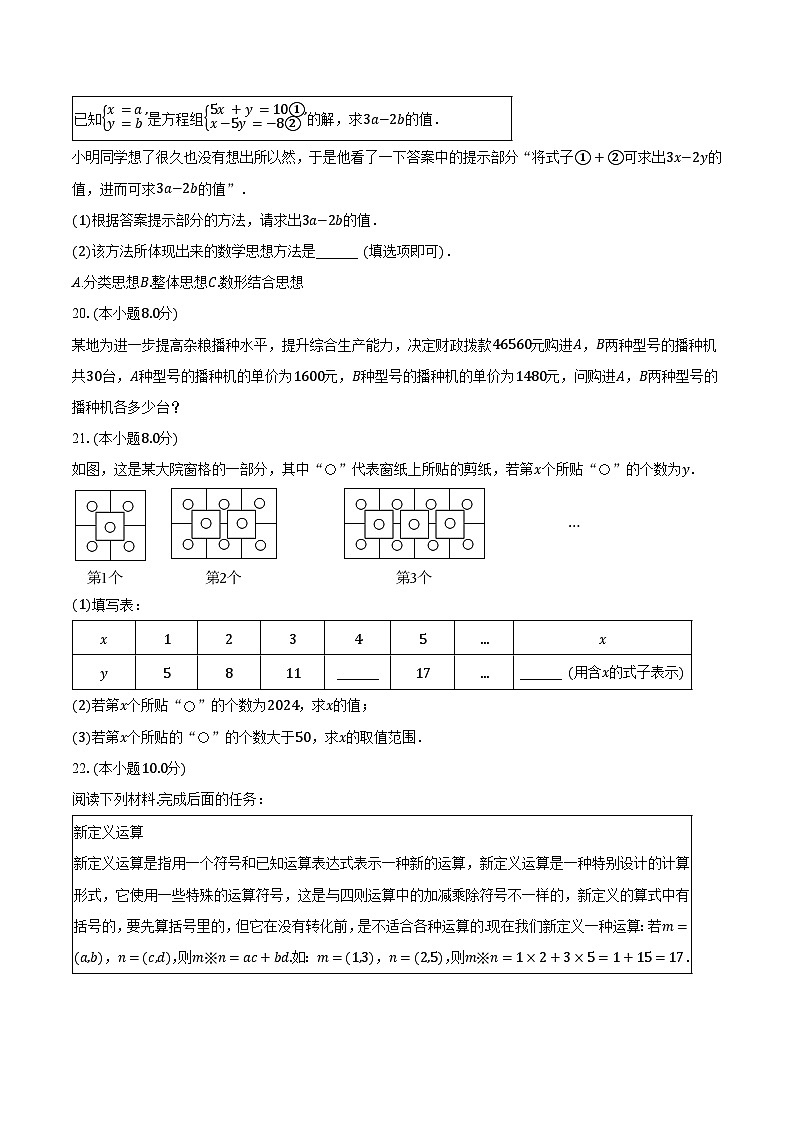
已知是方程组的解,求的值. |
小明同学想了很久也没有想出所以然,于是他看了一下答案中的提示部分“将式子可求出的值,进而可求的值”.
根据答案提示部分的方法,请求出的值.
该方法所体现出来的数学思想方法是______ 填选项即可.
A.分类思想整体思想数形结合思想
20.本小题分
某地为进一步提高杂粮播种水平,提升综合生产能力,决定财政拨款元购进,两种型号的播种机共台,种型号的播种机的单价为元,种型号的播种机的单价为元,问购进,两种型号的播种机各多少台?
21.本小题分
如图,这是某大院窗格的一部分,其中“”代表窗纸上所贴的剪纸,若第个所贴“”的个数为.
填写表:
______ | ______ 用含的式子表示 |
若第个所贴“”的个数为,求的值;
若第个所贴的“”的个数大于,求的取值范围.
22.本小题分
阅读下列材料完成后面的任务:
新定义运算 |
任务:
若,,则,求的值.
已知,,则,且,,,求,的值.
23.本小题分
如图,这是福州市某区正在修建的一所学校的示意图,该学校的占地是一个长方形,长为米,宽为米,计划在三块形状及大小相同的长方形空地阴影部分修建教学楼,将剩余两块形状及大小相同的空地作为操场,求每个操场的面积.
24.本小题分
如图,这是一架天平,天平左盘放有一个物体,质量为克,右盘放有一些砝码,每个砝码的质量为克,当右盘放有个相同的砝码时,天平处于平衡状态.
若,求天平处于平衡状态时的值.
若一个二元一次方程的解,,都是正整数,我们把,称为该方程的正整数解,如:方程的正整数解为,求天平处于平衡状态下的,的正整数值.
期中考试后,老师计划购买笔记本和圆珠笔给表现优秀的同学作为奖品,笔记本和圆珠笔的单价均为正整数若购买本笔记本,支圆珠笔,共需要元,求购买本笔记本和支圆珠笔的费用.
25.本小题分
问题情境:在数学活动课上,老师给出了两个二元一次方程:和.
问题解决:试用含的代数式分别表示 ______ , ______ ;当时,求的值.
问题探究:若有理数,满足等式,求,的值.
问题拓展:在的条件下,如图,小明家到学校有两段公路,,其中处有一图书馆,公路长米,公路长米,小明骑自行车从出发以米分的速度匀速滑公路,向处行驶,小康跑步从处出发以米分的速度匀速沿公路,向处行进若小明从处出发分钟后,小康从处出发那么小明出发多少分钟后两人在行进路线上相距米?
答案和解析
1.【答案】
【解析】解:由题意可知:,
,
故选:.
根据题意列出方程解出的值即可求出答案.
本题考查一元一次方程,解题的关键是熟练运用一元一次方程的解法,本题属于基础题型.
2.【答案】
【解析】解:方程组,
将得:.
故选:.
方程组两方程相加得到结果,即可作出判断.
此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
3.【答案】
【解析】解:,
,
故选:.
按照解一元一次不等式的步骤,进行计算即可解答.
本题考查了解一元一次不等式,熟练掌握解一元一次不等式的步骤是解题的关键.
4.【答案】
【解析】解:当时,方程左边,方程右边,,
方程左边方程右边,
是二元一次方程的解,选项A符合题意;
B.当时,方程左边,方程右边,,
方程左边方程右边,
不是二元一次方程的解,选项B不符合题意;
C.当时,方程左边,方程右边,,
方程左边方程右边,
不是二元一次方程的解,选项C不符合题意;
D.当时,方程左边,方程右边,,
方程左边方程右边,
不是二元一次方程的解,选项D不符合题意.
故选:.
将各选项中的数值,代入原方程,取使得方程左边方程右边的选项即可.
本题考查了二元一次方程的解,牢记“把方程的解代入原方程,等式左右两边相等”是解题的关键.
5.【答案】
【解析】解:物体的体积、质量与它的密度的关系为,将等式去分母得,其变形的依据是等式的性质.
故选:.
物体的体积、质量与它的密度的关系为,将等式去分母得,也就是等式的两边同时乘,所以变形的依据是等式的性质:等式两边乘同一个数或除以一个不为零的数,结果仍得等式.
此题主要考查了等式的性质和应用,解答此题的关键是要明确:等式的性质:等式两边加同一个数或式子结果仍得等式;等式的性质:等式两边乘同一个数或除以一个不为零的数,结果仍得等式.
6.【答案】
【解析】解:设这批货物共有吨,根据题意得:
,
解得:,
即:这批货物共有吨.
故选:.
设这批货物共有吨,根据第一次运走的货物第二次运走的货物货物总数,列出方程,求出的值即可得出答案.
此题考查了一元一次方程的应用,读懂题意,找出题目中的数量关系,列出方程是解题的关键,本题的等量关系是:第一次运走的货物第二次运走的货物剩下的货物货物总数.
7.【答案】
【解析】解:,
选项A不符合题意;
,
,
选项B不符合题意;
,
,
选项C不符合题意;
,
,
选项D符合题意.
故选:.
根据,应用不等式的性质,逐项判断即可.
此题主要考查了不等式的基本性质:不等式的两边同时加上或减去同一个数或同一个含有字母的式子,不等号的方向不变;不等式的两边同时乘或除以同一个正数,不等号的方向不变;不等式的两边同时乘或除以同一个负数,不等号的方向改变.
8.【答案】
【解析】解:,移项,得:,
解集为,
,
,
则关于的方程为,
解得:.
故选:.
先根据数轴得出不等式的解集为,由此确定的值,然后代入方程,解方程即可.
本题考查了一元一次不等式的解法,在数轴上表示不等式的解集以及一元一次方程的解法,正确确定的值是关键.
9.【答案】
【解析】解:由题意可得,
.
故选:.
根据“甲得到乙所有钱的一半,那么甲共有钱文;如果乙得到甲所有钱的,那么乙也共有钱文”可以列出方程组,从而可以解答本题.
本题考查由实际问题抽象出二元一次方程组,解答本题的关键是明确题意,列出相应的方程组.
10.【答案】
【解析】解::当方程组的解,的值互为相反数时,即,,得,,进而求得,故选项A不符合题意.
:当时,,得,,方程,故选项B不符合题意.
:,得,,则,故选项C符合题意.
:由可知,,所以无论取什么实数,的值都为,故选项D不符合题意.
故选:.
本题考查二元一次方程组的解法,解中含有未知数的解,,等形式的解.
本题考查二元一次方程组的解法,解中含有未知数的解,,等形式的解.解题的关键是能有灵活运用二元一次方程组进行变换,进而作答.
11.【答案】
【解析】解:方程是关于,的二元一次方程,
解得.
故答案为:.
根据二元一次方程的定义,即可求解.
本题主要考查了二元一次方程的定义,熟练掌握含有两个未知数,且未知数的次数均为的整式方程是二元一次方程是解题的关键.
12.【答案】
【解析】解:由题意得,的质量大于的质量.
故.
故答案为:.
根据天平可判断的质量大于的质量.
本题考查了有理数大小比较,掌握天平的使用方法是解答本题的关键.
13.【答案】
【解析】解:不等式的解集为,
,
.
故答案为:.
根据不等式的性质:不等式两边同时除以同一个正数,不等号的方向不变可得答案.
本题考查了不等式的解集,关键是掌握不等式的性质.
14.【答案】
【解析】解:将代入方程,得:,
解得:,
故答案为:.
将代入方程得到关于的方程,解之可得答案.
本题主要考查二元一次方程的解,使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解是解题的关键.
15.【答案】
【解析】解:设每块条形石吨,则象的体重为吨,
根据题意得,
解得,
,
答:象的体重为吨.
故答案为:.
设每块条形石吨,可得,解得,即可得象的体重为吨.
本题考查一元一次方程的应用,解题的关键是读懂题意,找到等量关系列出方程.
16.【答案】
【解析】解:方法:把方程组的解代入原方程组中得:,
此式代入所求的方程得:
,
解得,
故答案为:.
方法:方程组组的解是,每个方程左右两边同时除以,
可化为Ⅰ,
设,,
方程组Ⅰ可化为Ⅱ,
方程组Ⅲ的解是,
对照方程组Ⅱ和Ⅲ的特点,得,
,
,
故答案为:.
方法、把方程组的解是代入原方程组中可得到,再把关于的代数式代入所求的方程组即可得解.
方法、先将所求的方程组每个方程除以,得出新的方程组再和方程组对照,得出新方程组的解,即可得出结论.
本题考查了运用代入法解二元一次方程组的方法,解题时要根据方程组的特点进行有针对性的计算.
17.【答案】解:,
,
,
.
【解析】按照解一元一次方程的步骤:移项,合并同类项,系数化为,进行计算即可解答.
本题考查了解一元一次方程,熟练掌握解一元一次方程的步骤是解题的关键.
18.【答案】解:由题意知,
解得.
【解析】根据题意列出不等式,再移项、合并即可得出答案.
本题主要考查解一元一次不等式的基本能力,严格遵循解不等式的基本步骤是关键,尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变.
19.【答案】
【解析】解:,得
,
,
.
是方程组的解,
.
由解题过程可知,该方法所体现出来的数学思想方法是整体思想.
故选:.
先根据题目提供的方法求出的值,进而可求的值;
由求解过程可知解答本题的思想方法是整体思想.
本题考查了二元一次方程组的特殊解法,在求二元一次方程组中两个未知数的和或差的时候,有时可以采用把两个方程直接相加或相减的方法,而不必求出两个未知数的具体值.
20.【答案】解:设购进台种型号的播种机,台种型号的播种机,
根据题意得:,
解得:.
答:购进台种型号的播种机,台种型号的播种机.
【解析】设购进台种型号的播种机,台种型号的播种机,利用总价单价数量,结合该地财政拨款元购进,两种型号的播种机共台,可列出关于,的二元一次方程组,解之即可得出结论.
本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
21.【答案】
【解析】解:填表如下:
用含的式子表示 |
故答案为:,;
依题意有:,
解得.
故的值为;
依题意有:,
解得.
故的取值范围是.
第一个图中所贴剪纸“”的个数为;第二个图中所贴剪纸“”的个数为;第三个图中所贴剪纸“”的个数为;从而可以得出第个图中所贴剪纸“”的个数和第个图中所贴剪纸“”的个数为;
利用中的规律列出方程计算即可求解;
利用中的规律列出不等式计算即可求解.
此题考查一元一次不等式的应用,图形的变化规律.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,得出规律解决问题.
22.【答案】解:,,,
,
解得;
,,则,且,,,
,
解得,
即的值是,的值是.
【解析】根据题意,可以得到,然后求解即可;
根据题意可以得到,然后求解即可.
本题考查一元一次方程的应用、二元一次方程组的应用、新定义,解答本题的关键是明确新定义,列出相应的方程和方程组.
23.【答案】解:设阴影部分的小长方形的长为米,则小长方形的宽为米,
由宽米可列方程:,
解得:,
则,
阴影部分的小长方形的长为米,小长方形的宽为米,
两个操场的总面积为平方米,
每个操场的面积为平方米.
【解析】设阴影部分的小长方形的长为米,则小长方形的宽为米,利用大长方形的宽为米列出方程,求解的小长方形的长为米,小长方形的宽为米,则每个操场的面积大长方形的面积个小长方形的面积.
本题主要考查一元一次方程的应用,根据大长方形的长得出小长方形的长与宽之间的关系,再利用大长方形的宽列出方程,进而解决问题是解题关键.
24.【答案】解:由题意得:,
,
,
解得:,
即,天平处于平衡状态时的值为;
由题意得:,
即,
整理得:,
,为正整数,
;
设笔记本的单价为元,圆珠笔的单价为元,
由题意得:,
整理得:,
、为正整数,
或,
当,时,;
当,时,;
答:购买本笔记本和支圆珠笔的费用为元或元.
【解析】由题意得,再代入得,即可得出结论;
由题意得,求出正整数解即可;
设笔记本的单价为元,圆珠笔的单价为元,根据购买本笔记本,支圆珠笔,共需要元,列出二元一次方程,求出正整数解,即可解决问题.
本题考查了二元一次方程的应用,找准等量关系,正确列出二元一次方程是解题的关键.
25.【答案】
【解析】解:,
,
,
,
;
,
解得:;
故答案为:,;
,
且,
解得:,;
当相遇前相聚米,则,
解得:,
当相遇后相距米,则,
解得:,
相距米时,或.
将代数式变形,用含的式子表示,即可,当时,列出关于的方程即可;
根据绝对值和平方数的非负性,列出关于,的方程即可求解;
设小明出发分钟后两人相距米,分情况讨论列出相遇前和相遇后的方程,求解即可.
本题主要考查二元一次方程以及代数式的求值,正确根据题意列出方程是解题关键.
2023-2024学年福建省泉州市德化县七年级(上)期中数学试卷(含解析): 这是一份2023-2024学年福建省泉州市德化县七年级(上)期中数学试卷(含解析),共15页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年福建省泉州市德化县七年级(下)期末数学试卷(含解析): 这是一份2022-2023学年福建省泉州市德化县七年级(下)期末数学试卷(含解析),共19页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年福建省泉州市德化县七年级(下)期末数学试卷(含解析): 这是一份2022-2023学年福建省泉州市德化县七年级(下)期末数学试卷(含解析),共19页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












