2022-2023学年河南省郑州七中七年级（下）期中数学试卷（含解析）

这是一份2022-2023学年河南省郑州七中七年级（下）期中数学试卷（含解析），共17页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2022-2023学年河南省郑州七中七年级（下）期中数学试卷第I卷（选择题）一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）1.下列运算正确的是(    )A.  B.  C.  D. 2.下列图形中，表示和是对顶角的是(    )A.  B.
C.  D. 3.如图，把一块直角三角板的直角顶点放在直尺的一边上，若，则(    )
 A.  B.  C.  D. 4.若是关于的完全平方式，则常数的值为(    )A.  B. 或 C.  D. 5.如图，，平分，则下列结论不正确的是(    )A. 与互余
B. 与互余
C. 与互补
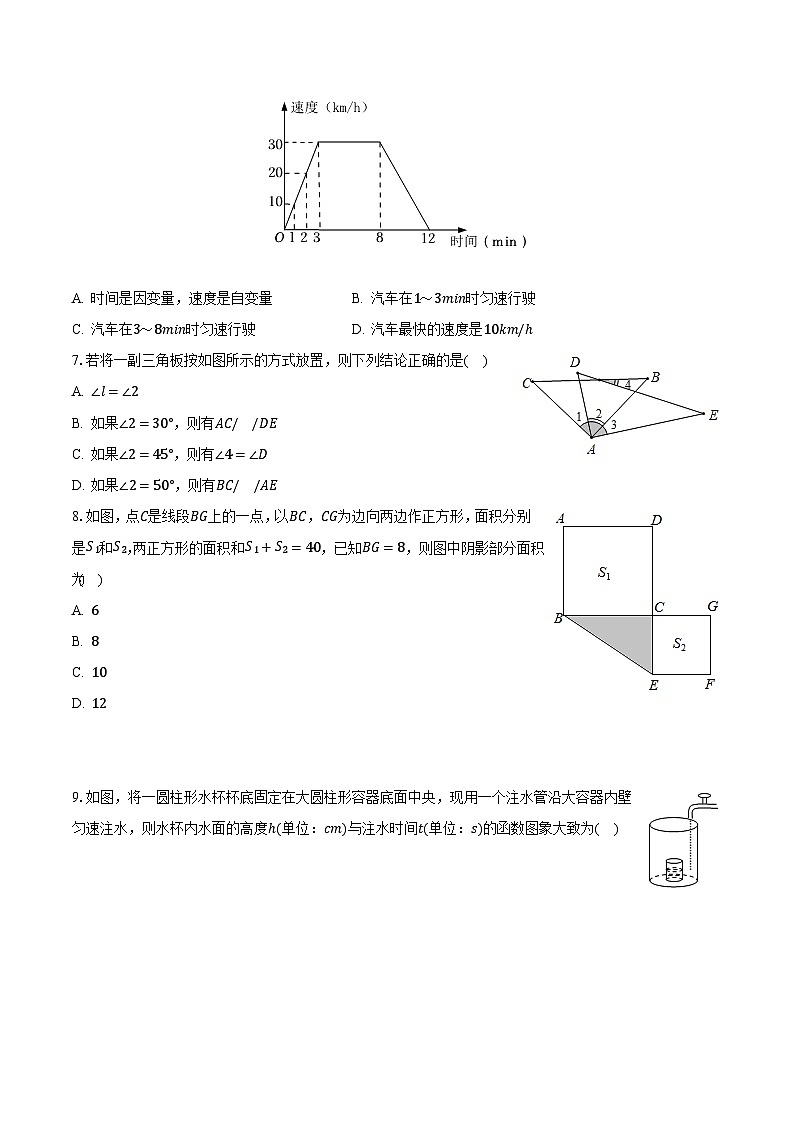
D. 图中没有互补的两个角6.一辆汽车行驶的速度与时间之间的变化关系如图所示，说法正确的是(    )
A. 时间是因变量，速度是自变量 B. 汽车在时匀速行驶
C. 汽车在时匀速行驶 D. 汽车最快的速度是7.若将一副三角板按如图所示的方式放置，则下列结论正确的是(    )A.
B. 如果，则有
C. 如果，则有
D. 如果，则有8.如图，点是线段上的一点，以，为边向两边作正方形，面积分别是和，两正方形的面积和，已知，则图中阴影部分面积为(    )A.
B.
C.
D.
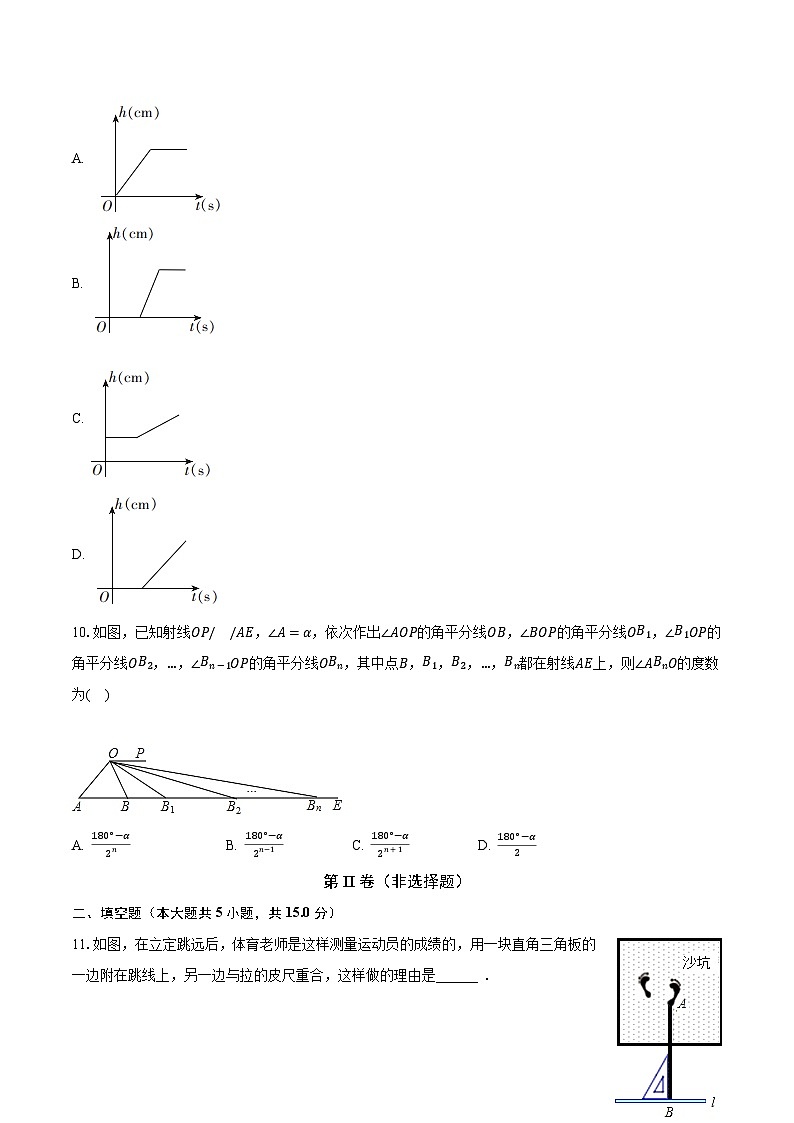
 9.如图，将一圆柱形水杯杯底固定在大圆柱形容器底面中央，现用一个注水管沿大容器内壁匀速注水，则水杯内水面的高度单位：与注水时间单位：的函数图象大致为(    )A.
B.
C.
D. 10.如图，已知射线，，依次作出的角平分线，的角平分线，的角平分线，，的角平分线，其中点，，，，都在射线上，则的度数为(    )

 A.  B.  C.  D. 第II卷（非选择题）二、填空题（本大题共5小题，共15.0分）11.如图，在立定跳远后，体育老师是这样测量运动员的成绩的，用一块直角三角板的一边附在跳线上，另一边与拉的皮尺重合，这样做的理由是______ ．
 12.随着人们对环境的重视，新能源的开发迫在眉睫，石墨烯是现在世界上最薄的纳米材料，其理论厚度应是，用科学记数法表示是          ．13.比较大小：______填“”、“”或“”14.某烤鸭店在确定烤鸭的烤制时间时，主要依据的是下表的数据：鸭的质量烤制时间若鸭的质量为时，烤制时间为______ ．15.如图，已知长方形纸带，将纸带沿折叠后，点、分别落在、的位置，再沿折叠成图，若，则 ______

 三、解答题（本大题共7小题，共55.0分。解答应写出文字说明，证明过程或演算步骤）16.本小题分
计算．17.本小题分
已知，试求的值．
已知，，求的值．18.本小题分

如图，点、分别在、上，于点，，，求证：请填空．
证明：已知
______
又______
____________
______
______
又______平角的定义
______
又已知
______
______内错角相等，两直线平行
19.本小题分

光线从空气中射入水中会发生折射现象，光线从水中射入空气中，同样会发生折射现象如图是光线从空气中射入水中，再从水中射入空气中的示意图已知，请你用所学知识来判断与是否平行？并说明理由．
20.本小题分

图是一个长为，宽为的长方形，相图中虚线用剪刀均分成四块小长方形，然后按图的形状拼成一个正方形．
求图中的阴影部分的正方形的周长；
观察图，请写出下列三个代数式，，之间的等量关系；
运用你所得到的公式，计算：若、为实数，且，试求的值．
21.本小题分
受疫情的影响，各类学校纷纷延迟开学时间，教育部提倡“停课不停教，停课不停学”的在线教学方式．寒假期间，线上教育的用户使用量猛增，现“钉钉”平台整理出“线上教学”项目投入资金及预计利润如表：投入资金亿元预计利润千万元如表反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？
如果预计获得千万元的利润，投入资金应为______亿元．
如果公司可以拿出亿元进行“线上教学”项目的投资，预计利润是多少？说说理由．22.本小题分
问题情境：如图，，，，求度数．
小明的思路是：过作，通过平行线性质来求．
按小明的思路，易求得的度数为______度；直接写出答案
问题迁移：如图，，点在射线上运动，记，，当点在、两点之间运动时，问与，之间有何数量关系？请说明理由；
在的条件下，如果点在、两点外侧运动时点与点、、三点不重合，请直接写出与，之间的数量关系．


答案和解析 1.【答案】 【解析】解：、，故A不符合题意；
B、，故B不符合题意；
C、，故C不符合题意；
D、，故D符合题意；
故选：．
利用单项式乘单项式的法则，负整数指数幂的法则，幂的乘方与积的乘方的法则对各项进行运算即可．
本题主要考查单项式乘单项式，幂的乘方与积的乘方，负整数指数幂，解答的关键是对相应的运算法则的掌握．2.【答案】 【解析】解：根据对顶角的定义可得、、都不是对顶角，只有选项符合对顶角的定义．
故选：．
两条直线相交后所得的只有一个公共顶点且两个角的两边互为反向延长线，这样的两个角叫做互为对顶角，由此可得出正确答案．
本题考查对顶角的定义，属于基础题，要求熟练掌握对顶角的定义．3.【答案】 【解析】解：如图，

，
，
．
故选：．
由互余可求得的度数，然后由两直线平行，同位角相等求得的度数．
此题考查了平行线的性质．两直线平行，同位角相等的应用是解此题的关键．4.【答案】 【解析】解：．
是关于的完全平方式，
．
．
当时，．
当时，．
综上：或．
故选：．
根据完全平方式的定义解决此题．
本题主要考查完全平方式的定义，熟练掌握完全平方式的定义是解决本题的关键．5.【答案】 【解析】解：与互余，说法正确，不符合题意；
与互余，说法正确，不符合题意；
与互补，说法正确，不符合题意；
D、图中没有互补的两个角，说法错误，符合题意；
故选：．
根据，，平分，可得，再根据，可得，然后根据余角定义和补角定义进行分析即可．
此题主要考查了余角和补角，关键是掌握余角：如果两个角的和等于直角，就说这两个角互为余角．即其中一个角是另一个角的余角；补角：如果两个角的和等于平角，就说这两个角互为补角．即其中一个角是另一个角的补角．6.【答案】 【解析】解：速度是因变量，时间是自变量，故选项A不合题意；
汽车在分钟时，速度在增加，故选项B不合题意；
汽车在分钟，匀速运动，故选项C符合题意；
汽车最快速度是千米时，故选项D不符合题意；
故选：．
观察图象，结合题意，明确横轴与纵轴的意义，依次分析选项可得答案．
本题考查了函数的图象，解决本题的关键是读懂图意，明确横轴与纵轴的意义．7.【答案】 【解析】解：，
，故A错误．
，

，
，
，故B正确，
，
，
，
，
，
，故C错误，
，
，
，
不平行，故D错误．
故选：．
根据平行线的判定和性质一一判断即可
本题考查平行线的性质和判定，解题的关键是熟练掌握基本知识，属于中考常考题型．8.【答案】 【解析】解：设，，则，，．
．
，
，
，
阴影部分的面积等于．
故选：．
设，，建立关于，的关系，最后求面积．
本题考查完全平方公式的几何背景，通过面积关系构造使用完全平方公式的条件是求解本题的关键．9.【答案】 【解析】解：当注入大圆柱形容器的水面高度到达小水杯的高度前，水杯内水面的高度为，故选项A、不合题意；
当注入大圆柱形容器的水面高度到达小水杯的高后，水杯内水面的高度逐渐增大，当水杯内水面的高度达到水杯高度时，水杯内水面的高度不再增加，故选项B符合题意，选项D不合题意．
故选：．
根据注水情况分析即可得到函数的图象．
本题考查了函数的图象．正确理解函数图象横纵坐标表示的意义，理解问题的过程，能够判断出函数随自变量的增大，是增大还是减小的，是解答本题的关键．10.【答案】 【解析】解：因为，
所以，
因为平分，，
所以，
因为，
所以，
所以，
同理可得，，，
则．
故选：．
根据角平分线的定义和平行线的性质得到规律，即可求得的度数．
本题考查了平行线的性质，角平分线的性质，熟练掌握性质定理是解题的关键．11.【答案】垂线段最短 【解析】解：如图，在立定跳远后，体育老师是这样测量运动员的成绩的，用一块直角三角板的一边附在跳线上，另一边与拉的皮尺重合，这样做的理由是垂线段最短．
故答案为：垂线段最短
利用点到直线的距离中垂线段最短判断即可．
此题考查了垂线段最短，点到直线的所有连线中，垂线段最短．12.【答案】 【解析】解：，
故答案为：
绝对值小于的正数也可以利用科学记数法表示，一般形式为，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的的个数所决定．
本题考查用科学记数法表示较小的数，一般形式为，其中，为由原数左边起第一个不为零的数字前面的的个数所决定．13.【答案】 【解析】解：，．
，
．
．
故答案为：．
根据幂的乘方可得即可解决此题．
本题主要考查幂的乘方，有理数大小的比较，熟练掌握幂的乘方是解决本题的关键．14.【答案】 【解析】解：由表格数据知与的函数表达式为：．
当时，分钟．
故答案为：．
根据题意得出函数表达式，再通过函数表达式即可计算．
本题考查一次函数的应用，根据题意求出函数表达式是求解本题的关键．15.【答案】 【解析】解：，
，，
即，，
．
，
．
由折叠可得：，
．
故答案为：．
先根据求出的度数，进可得出和的度数，根据和三角形的内角和可得的度数，再由折叠的性质可得．
本题考查的是平行线的性质，由折叠的性质得到角相等是解题关键．16.【答案】解：


． 【解析】先化简各式，然后再进行计算即可解答．
本题考查了有理数的加法，乘法，乘方，零指数幂，负整数指数幂，绝对值，准确熟练地化简各式是解题的关键．17.【答案】解：


，
，
，
，
的值为；
，
，，
，
的值为． 【解析】，再代入求值即可；
，再代入求值即可．
本题考查了幂的乘方，熟练掌握幂的乘方运算是解本题的关键，综合性较强，难度适中．18.【答案】垂直的定义  已知    同位角相等，两直线平行  两直线平行，同位角相等  等量代换      同角的余角相等   【解析】证明：已知，
垂直的定义．
又已知，
同位角相等，两直线平行，
两直线平行，同位角相等，
等量代换．
又平角的定义，
．
又已知，
同角的余角相等，
内错角相等，两直线平行．
故答案为：垂直的定义；已知；；同位角相等，两直线平行；两直线平行，同位角相等；等量代换；；；同角的余角相等；．
先证得，由得，利用平角定义得出，结合可以得出，从而得证．
本题主要考查平行线的判定与性质，解题的关键是掌握平行线的判定和性质，并灵活运用．19.【答案】解：；
理由如下：
如图，，，
，
，
等式的性质，
内错角相等，两直线平行． 【解析】欲证明，结合图形只要先证明，再利用内错角相等，两直线平行即可．
本题考查平行线的判定定理，正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键，不能遇到相等或互补关系的角就误认为具有平行关系，只有同位角相等、内错角相等、同旁内角互补，才能推出两被截直线平行．20.【答案】解：由拼图可知，图中阴影部分的正方形的边长为，因此周长为；
答；图中的阴影部分的正方形的周长为；
图整体大正方形的边长为，因此面积为，阴影部分正方形的边长为，因此面积为，四个长方形的面积为，由面积之间的关系可得；
由可得，；
，，
，
或． 【解析】由拼图可得阴影正方形的边长，进而表示周长即可；
根据图形中各个部分面积之间的关系即可得出答案；
由的结论代入计算即可．
本题考查完全平方公式的几何背景，掌握完全平方公式的结构特征是正确解答的前提．21.【答案】 【解析】反映了投入资金和预计利润之间的关系，投入资金是自变量，预计利润是因变量；

从表格数据看，如果预计获得千万元的利润，投入资金应为亿元，
故答案为；

从表格数据看，与之间的关系为，
当时，，
故预计利润是千万元．
根据函数的定义即可求解；
查表格数据即可求解；
从表格数据看，与之间的关系为，进而求解．
本题考查了函数的表示方法，解决本题的关键是列出函数关系式．22.【答案】解：；
，
理由：如图，过作交于，

，
，
，，
；
或． 【解析】【分析】
本题主要考查了平行线的性质和判定的应用，主要考查学生的推理能力，题目是一道比较典型的题目，解题时注意分类思想的运用．
过作，通过平行线性质求即可；
过作交于，推出，根据平行线的性质得出，，即可得出答案；
分两种情况：在延长线上；在延长线上，分别画出图形，根据平行线的性质得出，，即可得出答案．
【解答】
解：过点作，
，
，
，，
，，
，，
．
故答案为：．
见答案；如图所示，当在延长线上时，过点作，
，
，
，，
；

如图所示，当在延长线上时，．

综上，或．