2022-2023学年浙江省金华市义乌市稠州中学教育集团七年级（下）独立作业数学试卷（5月份）（含解析）

2022-2023学年浙江省金华市义乌市稠州中学教育集团七年级（下）独立作业数学试卷（5月份）

一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）

1.如图，已知，，则的度数为(    )
 

A.
B.
C.
D.

2.下列方程是二元一次方程的是(    )

A.  B.  C.  D.

3.观察下面图案，在、、，四幅图案中，能通过如图图案的平移得到的是(    )

A.  B.  C.  D.

4.的计算结果为(    )

A.  B.  C.  D.

5.若分式有意义，则应满足的条件是(    )

A.  B.  C.  D.

6.某个机器零件的直径为，用科学记数法表示为(    )

A.  B.  C.  D.

7.下列式子中能用完全平方公式分解因式的是(    )

A.  B.  C.  D.

8.小亮解方程组的解为，由于不小心滴上了两滴墨水，刚好遮住了两个数和，则这两个数分别为(    )

A. 和 B. 和 C. 和 D. 和

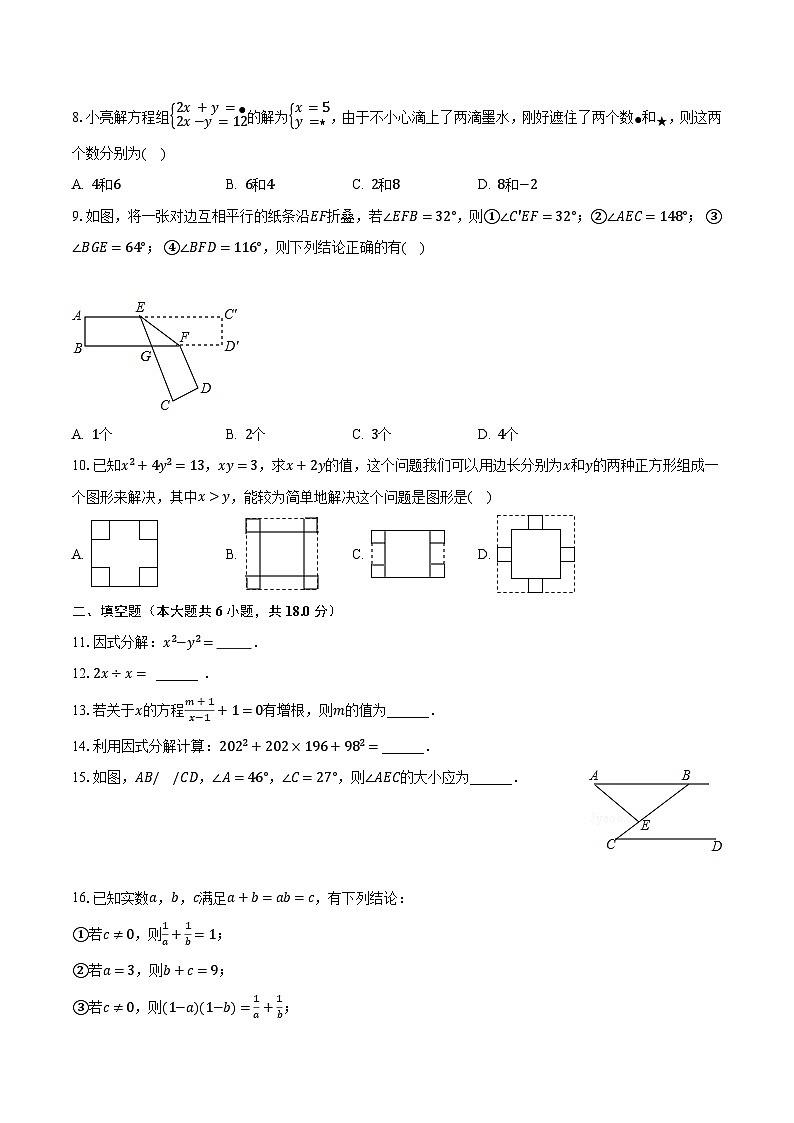
9.如图，将一张对边互相平行的纸条沿折叠，若，则；； ； ，则下列结论正确的有(    )

 

A. 个 B. 个 C. 个 D. 个

10.已知，，求的值，这个问题我们可以用边长分别为和的两种正方形组成一个图形来解决，其中，能较为简单地解决这个问题是图形是(    )

A.  B.  C.  D.

二、填空题（本大题共6小题，共18.0分）

11.因式分解：          ．

12. ______ ．

13.若关于的方程有增根，则的值为______．

14.利用因式分解计算：______．

15.如图，，，，则的大小应为______．

16.已知实数，，满足，有下列结论：
若，则；
若，则；
若，则；
若，则．
其中正确的是 ______ 把所有正确结论的序号都填上．

三、解答题（本大题共8小题，共52.0分。解答应写出文字说明，证明过程或演算步骤）

17.本小题分
计算：
；
．

18.本小题分
若，求的值．
先化简分式，再从，，，四个数中选一个恰当的数作为的值，代入求值．

19.本小题分
因式分解
；
．

20.本小题分
解方程或方程组

．

21.本小题分

如图，已知：，，求证：，下面是不完整的说明过程，请将过程及其依据补充完整．
证明：已知
______ ______
______
又已知
______ ______
______

22.本小题分
某工厂承接了一批纸箱加工任务，用如图所示的长方形和正方形纸板长方形的宽与正方形的边长相等加工成如图所示的竖式与横式两种无盖的长方形纸箱．加工时接缝材料不计
该工厂原计划用若干天加工纸箱个，后来由于对方急需要货，实际加工时每天加工速度时原计划的倍，这样提前天超额完成了任务，且总共比原计划多加工个，问原计划每天加工纸箱多少个；
若该厂购进正方形纸板张，长方形纸板张．问竖式纸盒，横式纸盒各加工多少个，恰好能将购进的纸板全部用完．

 

23.本小题分
已知关于的分式方程．
当时，求方程的解．
若该方程去分母后所得的整式方程的解是增根，求的值．
关于的方程有整数解，求此时整数的值．

24.本小题分
设三角形三内角的度数分别为、、，如果其中一个角的度数是另一个角度数的倍，那么我们称这个三角形为“和谐三角形”，并把满足条件的、、称为“和谐三角形”的一组值例如，，为“和谐三角形”的一组值．
当，写出以为其中一个内角的“和谐三角形”的一组值；
当时，符合条件的“和谐三角形”是否只有一组值，写出你的判断并用含的代数式表示、；
为何值时，符合条件的“和谐三角形”分别有一组、二组、三组值？请你分别写出对应的值或范围直接填在下表中．

答案和解析

1.【答案】 

【解析】【分析】
先根据对顶角相等，，求出的度数，再由两直线平行，同旁内角互补得出的度数．
本题考查的是平行线的性质，用到的知识点为：两直线平行，同旁内角互补．
【解答】
解：，，
，
．
故选：．

2.【答案】 

【解析】解：、是整式，不是方程，不符合题意；
B、是二元一次方程，符合题意；
C、是分式方程，不符合题意；
D、是二元二次方程，不符合题意．
故选：．
根据二元一次方程的定义解答即可．
本题考查的是二元一次方程的定义，熟知含有两个未知数，并且含有未知数的项的次数都是，像这样的方程叫做二元一次方程是解题的关键．

3.【答案】 

【解析】解：图与原图上下方向相反，不是原图平移后的图形，不合题意；
B.图与原图左右方向相反，不是原图平移后的图形，不合题意；
C.图与原图方向相同，是原图平移后的图形，符合题意；
D.图与原图上、下方向，左、右方向都相反，是原图旋转后的图形，不合题意．
故选：．
根据图形平移的特征，将一个图形上的所有点都按照某个方向作相同距离的移动，这样的图形运动叫作图形的平移．平移不改变图形的形状、大小和方向，进而判断即可．
此题主要考查了利用平移设计图案，正确掌握平移的性质是解题关键．

4.【答案】 

【解析】【分析】
根据幂的乘方性质计算后即可判定选项．
此题比较简单，直接利用幂的乘方法则计算即可得到结果．
【解答】
解：．
故选C．

5.【答案】 

【解析】解：若分式有意义，
则，
解得：，
故选：．
直接利用分式有意义则分母不等于零进而得出答案．
此题主要考查了分式有意义的条件，正确把握分式有意义则分母不等于零是解题关键．

6.【答案】 

【解析】解：
故选：．
科学记数法的表示形式为的形式，其中，为整数．确定的值时，要看把原数变成时，小数点移动了多少位，的绝对值与小数点移动的位数相同．当原数绝对值时，是正整数，当原数绝对值时，是负整数．
此题主要考查了用科学记数法表示较大的数，一般形式为，其中，确定与的值是解题的关键．

7.【答案】 

【解析】解：因为、中间项不是、的积的倍，中间项不是、的倍，
所以选项A、、不符合完全平方公式的结构特点，不能用完全平方公式分解；
，故选项C能用完全平方公式分解因式．
故选：．
根据完全平方公式的结构特点逐个分析得结论．
本题考查了因式分解的完全平方公式，掌握完全平方公式的结构特点是解决本题的关键．

8.【答案】 

【解析】解：是方程组的解，
，，
，
是，是．
故选：．
根据是方程组的解，把代入方程求出的值，再把、的值代入即可．
此题比较简单，只要把已知结果代入原方程组进行计算即可．

9.【答案】 

【解析】【分析】
本题考查的是平行线的性质及翻折变换的性质，熟知图形翻折不变的性质是解答此题的关键．根据平行线的性质及翻折变换的性质对各小题进行逐一分析即可．
【解答】
解：因为，，
所以，故正确；
因为，，
所以，
因为，
所以，故错误；
因为，
所以，
所以，
因为，
所以，故正确；
因为，
所以，
因为，
所以，故正确．
故选C．

10.【答案】 

【解析】解：．
故选：．
根据完全平方公式得到：，即可解答．
本题考查了完全平方公式的几何背景，解决本题的关键是熟记完全平方公式．

11.【答案】 

【解析】【分析】
直接利用平方差公式分解因式得出即可．
此题主要考查了利用公式法分解因式，熟练掌握平方差公式是解题关键．
【解答】
解：．
故答案为：．

12.【答案】 

【解析】解：原式



，
故答案为：．
根据单项式除以单项式法则：系数相除，同底数幂相除，然后计算即可．
本题主要考查了整式的除法运算，解题关键是熟练掌握单项式除以单项式法则．

13.【答案】 

【解析】解：去分母得：，
由分式方程有增根，得到，即，
把代入整式方程得：，
故答案为：
分式方程去分母转化为整式方程，由分式方程有增根，得到，求出的值，代入整式方程即可求出的值．
此题考查了分式方程的增根，增根问题可按如下步骤进行：让最简公分母为确定增根；化分式方程为整式方程；把增根代入整式方程即可求得相关字母的值．

14.【答案】． 

【解析】【分析】
这是一道考查因式分解的应用的题目，运用公式法可以简便计算一些式子的值．通过观察，显然符合完全平方公式．
【解答】
解：原式


．
故答案为．

15.【答案】 

【解析】解：，
，
；
故答案为：．
由平行线的性质得出，再由三角形的外角性质得出即可．
本题考查了平行线的性质、三角形的外角性质；熟练掌握平行线的性质和三角形的外角性质是解决问题的关键．

16.【答案】 

【解析】解：，，
，
等式两边同除以得：
，
．
的结论正确；
若，，
，
，，
．
的结论不正确；
，，
．
由知：，
若，则，
的结论正确；
若，，
，
，
．
的结论正确．
综上，正确的是：．
故答案为：．
利用等式的性质对每个结论进行逐一判断即可得出结论．
本题主要考查了代数式求值，等式的性质，完全平方公式，整式的乘除，熟练掌握等式的性质是解题的关键．

17.【答案】解：原式
；
原式

． 

【解析】直接利用绝对值，负整数指数幂的性质以及零指数幂的性质分别化简得出答案；
直接利用完全平方公式和平方差公式展开，再合并同类项即可．
此题主要考查了绝对值，负整数指数幂的性质以及零指数幂的性质以及完全平方公式和平方差公式，熟练掌握运算法则和公式是解题关键．

18.【答案】解：，
，




；


，
当，时，原分式无意义，
，
当时，原式． 

【解析】根据，可以得到，然后代入所求式子计算即可；
先算括号内的式子，再算括号外的除法，最后从，，，四个数中选一个使得原分式有意义的值代入化简后的式子即可．
本题考查分式的化简求值，熟练掌握运算法则是解答本题的关键．

19.【答案】解：；

． 

【解析】利用完全平方公式直接分解；
先提取公因式，再利用平方差公式分解．
本题考查了整式的因式分解，掌握因式分解的提公因式法和公式法是解决本题的关键．

20.【答案】解：，
得：，
解得：，
把代入得：，
解得：，
则方程组的解为；
去分母得：，
解得：，
检验：当时，，
是原方程的根． 

【解析】利用加减消元法求出解即可；
按照解分式方程的步骤，进行计算即可解答．
此题考查了解二元一次方程组，以及解分式方程，熟练掌握各自的解法是解本题的关键．

21.【答案】；内错角相等，两直线平行；两直线平行，内错角相等；；等量代换；同位角相等，两直线平行 

【解析】证明：已知
内错角相等，两直线平行
两直线平行，内错角相等
又已知
等量代换
同位角相等，两直线平行．
故答案为：；内错角相等，两直线平行；两直线平行，内错角相等；；等量代换；同位角相等，两直线平行．
由已知一对内错角相等得到与平行，利用两直线平行同位角相等得到一对角相等，再由已知另一对角相等，等量代换得到一对同位角相等，利用同位角相等两直线平行即可得证．
此题考查了平行线的判定与性质，熟练掌握平行线的判定与性质是解本题的关键．

22.【答案】解：设原计划每天加工个，则现在每天加工个，
由题意得，，
解得：，
经检验：是原分式方程的解，且符合题意，
答：原计划每天加工个；
设加工竖式纸盒个，横式纸盒个，
由题意得，，
解得：．
答：加工竖式纸盒个，横式纸盒个恰好能将购进的纸板全部用完． 

【解析】设原计划每天加工个，则现在每天加工个，根据题意可得，现在加工个比原计划加工个少用天，据此列方程求解；
设加工竖式纸盒个，横式纸盒个，根据正方形纸板有张，长方形纸板有张列方程组求解．
本题考查了分式方程和二元一次方程组的应用，解答本题的关键是读懂题意，设出未知数，找出合适的等量关系，列方程求解．

23.【答案】解：当时，分式方程为：，
，
解得：，
检验：当时，，
是原方程的根；
，
，
解得：，
由题意得：，
解得：，
，
解得：，
的值为；
，
，
解得：，
方程有整数解，
或且，
解得：或或或且，
或或，
此时整数的值为或或． 

【解析】把代入原方程中，然后按照解分式方程的步骤进行计算，即可解答；
先解分式方程可得，再根据题意得：，从而可得，然后进行计算即可解答；
先解分式方程可得：，再根据题意可得或且，然后进行计算即可解答．
本题考查了分式方程的增根，分式方程的解，准确熟练地进行计算是解题的关键．

24.【答案】     

【解析】解：，，或，，．
只有一组，，．
时，只有一组．
时，有二组．
时，有三组．
故答案分别为，，．
有两种切线是的三倍，是的三倍．
只有一种情形，是的三倍，构建三角形内角和定理即可解决问题．
根据，，由此即可解决问题．
本题考查三角形内角和定理、解题的关键是理解题意，考虑问题要全面，不能漏解，属于中考创新题目．