陕西省宝鸡市2023年八年级上学期期中数学试题（附答案）

这是一份陕西省宝鸡市2023年八年级上学期期中数学试题（附答案），共12页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
1．古埃及人曾经用如图所示的方法画直角：把一根长绳打上等距离的13个结，然后以3个结间距，4个结间距，5个结间距的长度为边长，用木桩钉成一个三角形，其中一角便是直角，这样做的道理是（ ）
A．直角三角形两个锐角互余
B．三角形内角和等于180°
C．三角形两边之和大于第三边，两边之差小于第三边
D．如果三角形两边的平方和等于第三边的平方，那么这个三角形是直角三角形
2．如图，Rt△ABC中，∠ACB＝90°，若AB＝15cm，则正方形ADEC和正方形BCFG的面积之和为（ ）
A．150cm2B．200cm2C．225cm2D．无法计算
3．如图，小手盖住的点的坐标可能为（ ）
A．B．C．D．
4．下列说法中，不正确的是（ ）
A．10的立方根是B．是4的一个平方根
C．的平方根是D．0.01的算术平方根是0.1
5．下列计算结果正确的是（ ）
A．B． =±6
C．D．
6．已知点 、点 在一次函数 的图像上，且 ，则m的取值范围是（ ）
A．B．C．D．
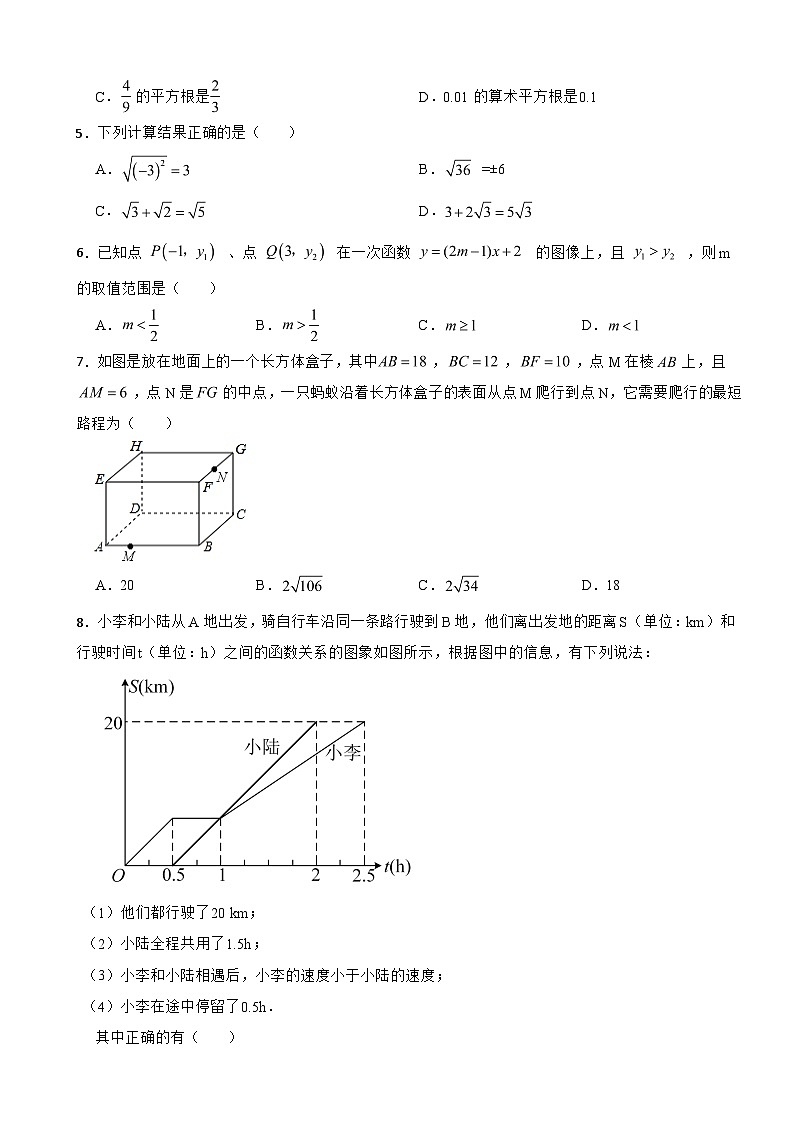
7．如图是放在地面上的一个长方体盒子，其中，，，点M在棱上，且，点N是的中点，一只蚂蚁沿着长方体盒子的表面从点M爬行到点N，它需要爬行的最短路程为（ ）
A．20B．C．D．18
8．小李和小陆从A地出发，骑自行车沿同一条路行驶到B地，他们离出发地的距离S（单位：km）和行驶时间t（单位：h）之间的函数关系的图象如图所示，根据图中的信息，有下列说法：
（1）他们都行驶了20 km；
（2）小陆全程共用了1.5h；
（3）小李和小陆相遇后，小李的速度小于小陆的速度；
（4）小李在途中停留了0.5h．
其中正确的有（ ）
A．4个B．3个C．2个D．1个
二、填空题
9．若点A（﹣2，a）与点B（2，4）关于y轴对称，则a的值为 ．
10．若函数y=(k+1)x+k2-1是正比例函数，则k的值为 。
11．如图，一个长方体铁盒的长，宽，高分别是8 cm，6 cm，24 cm，-根长28 cm的木棒 完全装进这个盒子里.（填“能”或“不能”）
12．如图，正方形ODBC中，OC=1，OA=OB，则数轴上点A表示的数是 ．
13．把两个同样大小的含45°角的三角尺按如图所示的方式放置，其中一个三角尺的锐角顶点与另一个的直角顶点重合于点A，且另三个锐角顶点B，C，D在同一直线上．若AB= ，则CD= ．
三、解答题
14．计算：
（1）；
（2）．
15．已知三个村庄A，B，C之间的距离分别为，，，现要从村修一条公路直达，已知公路造价为每千米39000元，求修这条公路的最低造价.
16．已知的平方根是±2，的立方根是3.
（1）求的值；
（2）求的算术平方根.
17．如图，△ABC中，AB＝AC＝13，BC＝24，请你建立适当的平面直角坐标系，并直接写出A，B，C三点的坐标．
18．如下图，已知每个小正方形的面积都为1，给出点C，请你按要求设计△ABC，使∠C＝90°，AC＝BC．
（1）AB的长为无理数，AC，BC的长均为有理数；
（2）AB的长为有理数，AC，BC的长均为无理数；
（3）三边的长均为无理数．
19．学完勾股定理之后，同学们想利用升旗的绳子、卷尺，测算出学校旗杆的高度．爱动脑筋的小明这样设计了一个方案：如图，小亮将升旗的绳子拉直到末端刚好接触地面，测得此时绳子末端距旗杆底端1米，然后将绳子末端拉直到距离旗杆5m处，测得此时绳子末端距离地面高度为1m，如果设旗杆的高度为x米（滑轮上方的部分忽略不计），求x的值．
20．如图，大拇指与小拇指尽量张开时，两指尖的距离称为指距．某项研究表明，一般情况下人的身高h是指距d的一次函数．下表是测得的指距与身高的一组数据：
（1）求出h与d之间的函数关系式；（不要求写出自变量d的取值范围）
（2）小明身高为142cm，一般情况下他的指距应是多少cm?
21．如图，已知火车站的坐标为，文化宫的坐标为．
( 1 )请你根据题目条件，画出平面直角坐标系；
( 2 )写出体育馆、市场、超市、医院的坐标；( 3 )请将原点O、医院C和文化宫B看作三点用线段连起来得，画出关于x轴对称的图形．
22．如图，折叠长方形一边AD，点D落在BC边的点F处，BC=10cm，AB=8cm，求：
（1）FC的长；
（2）EF的长．
23．在平面直角坐标系中有三点，点，点以及点C，已知点C与点A关于x轴对称．
（1）在平面直角坐标系中描出点A、B、C的位置，连接AB、AC、BC，画出△ABC的BC边上的中线AE，请直接写出点E的坐标为 ；
（2）求△ABE的面积．
24．甲、乙两地相距300km，一辆货车和一辆轿车先后从甲地出发向乙地．如图，线段OA表示货车离甲地距离y(km)与时间x(h)之间的函数关系，折线BCDE表示轿车离甲地距离y(km)与时间x(h)之间的函数关系．请根据图象，解答下列问题：
（1）线段CD表示轿车在途中停留了 h；
（2）求线段DE对应的函数解析式；
（3）求轿车从甲地出发后经过多长时间追上货车．
25．如图，L1，L2分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费，单位：元)与照明时间x(h)的函数图象，假设两种灯的使用寿命都是2000h，照明效果一样.
（1）根据图像分别求出L1，L2的函数关系式。
（2）当照明时间为多少时，两种灯的费用相等?
（3）小亮房间计划照明2500h，他买了一个白炽灯和一个节能灯，请你帮他设计最省钱的用灯方法(直接给出答案，不必写出解答过程).
1．D
2．C
3．D
4．C
5．A
6．A
7．A
8．A
9．4
10．1
11．不能
12．
13． ﹣1
14．（1）解：原式
；
（2）解：原式
．
15．解：如图，过点B作于点D，
因为，，，
所以，
所以为直角三角形，且.
因为.
所以.
（元）.
所以修这条公路的最低造价是180000元.
16．（1）解：∵x-2的平方根是±2，2x+y+7的立方根是3，
∴x-2=4，2x+y+7=27，
解得x=6，y=8；
（2）解：由（1）知x=6，y=8，
∴x2+y2=62+82=100，
∴x2+y2的算术平方根是10．
17．解：答案不唯一，如以BC所在直线为x轴，过点B作BC的垂线为y轴建立平面直角坐标系，
由图可知，点A(12，5)，B(0，0)，C(24，0)．
18．（1）解：如图所示，BC＝AC＝3，则；
(答案不唯一)
（2）解：如图所示，，则AB＝4；
(答案不唯一)
（3）解：如图所示，，则．
(答案不唯一)
19．解：设旗杆高度为x，可得AC＝AD＝x，AB＝（x﹣1）m，BC＝5m
根据勾股定理得，绳长的平方＝x2+12，
根据勾股定理得，绳长的平方＝（x﹣1）2+52，
∴x2+12＝（x﹣1）2+52，解得x＝12.5．
答：x值为12.5。
20．（1）解：设h与d之间的函数关系式为：．（k≠0）
把d＝20，h＝160；d＝21，h＝169，
分别代入得，．
解得k＝9，b＝－20，即h＝9d－20；
（2）解：当h＝142时，142＝9d－20，解得d＝18cm，
所以，一般情况下他的指距是18cm．
21．解：（1）平面直角坐标系如图所示．
（2）体育馆，市场，超市，医院．
（3）∵点B与B1，点C与C1关于x轴对称，B（-1，2），C（4，3），
∴B1（-1，-2），C1（4，-3），
∴，如图所示．
22．（1）解：由题意可得，AF=AD=10cm，
在Rt△ABF中，∵AB=8，
∴BF=6cm，
∴FC=BC﹣BF=10﹣6=4cm
（2）解：由题意可得EF=DE，可设DE的长为x，
则在Rt△EFC中，
（8﹣x）2+42=x2，
解得x=5，
即EF的长为5cm
23．（1）∵点C与点A关于x轴对称，且点A坐标为，
∴．
如图所示，依次在图中描出点A、点B与点C并连接即可．
（2）解：，，，
，
是BC边上的中线，
．
24．（1）0.5
（2）解：设线段DE对应的函数解析式为y=kx+b（2.5≤x≤4.5），
∵D点坐标为（2.5，80），E点坐标为（4.5，300），
∴代入y=kx+b，得： ，解得：．
∴线段DE对应的函数解析式为：y=110x－195（2.5≤x≤4.5）．
（3）解：设线段OA对应的函数解析式为y=mx（0≤x≤5），
∵A点坐标为（5，300），代入解析式y=mx得，300=5m，解得：m=60．
∴线段OA对应的函数解析式为y=60x（0≤x≤5）
由60x=110x－195，解得：x=3.9．
答：轿车从甲地出发后经过3.9小时追上货车．
25．（1）解：设l1的解析式为y1=k1x+2，
将点（500，17）代入得17=500k1+2，
解得k1=0.03，
∴y1=0.03x+2(0≤x≤2000)；
设l2的解析式为y2=k2x+20，
将点（500，26）代入得26=500k2+20，
解得k2=0.012，
∴y2=0.012x+20(0≤x≤2000)；
（2）解： 当y1=y2时，两种灯的费用相等，
∴0.03x+2=0.012x+20，
解得x=1000，
∴当照明时间为1000h时，两种灯的费用相等；
（3）解：分类讨论：①白炽灯使用2000h，节能灯使用500h时费用为：0.03×2000+2+0.012×500+20=88(元)；
②节能灯使用2000h，白炽灯使用500h时费用为：0.0 3×500+2+0.012×2000+20=61(元)；
③白炽灯使用1000h，节能灯使用1500h时费用为：0. 03×1000+2+0.012×1500+20=70(元)；
④白炽灯使用1500h，节能灯使用1000h时费用为：0. 03×1500+2+0.012×1000+20=79(元)，
∴节能灯使用2000h，白炽灯使用500h费用最低.指距d（cm）
20
21
22
23
身高h（cm）
160
169
178
187