广西柳州市2023—2024学年九年级上学期数学期中考试模拟卷

这是一份广西柳州市2023—2024学年九年级上学期数学期中考试模拟卷，共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
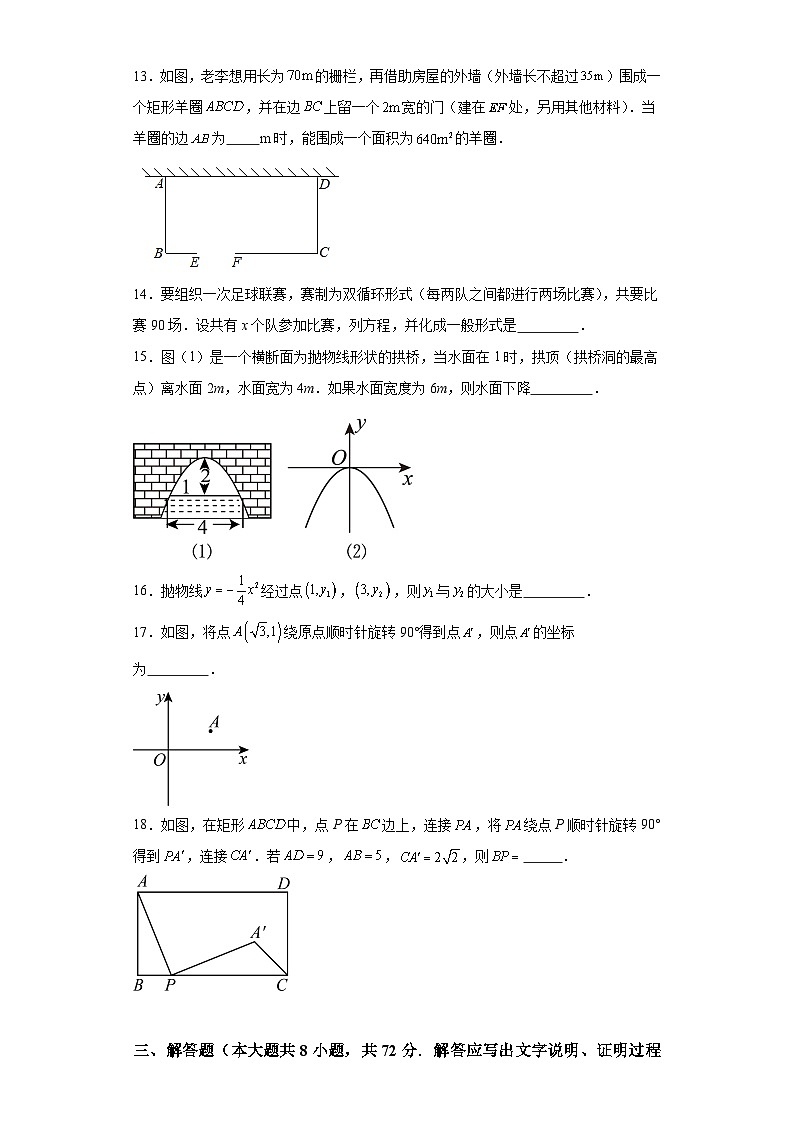
广西柳州市2023-2024学年九年级上册数学期中考试模拟卷（考试时间：120分钟  满分：120分）注意：本试卷分试题卷和答题卡两部分，答案一律填写在答题卡上，在试题卷上作答无效；不能使用计算器；考试结束后，将本试题卷和答题卡一并交回．第Ⅰ卷一、选择题（共12小题，每小题3分，共36分．在每小题给出的四个选项中只有一项是符合要求的，用2B铅笔把答题卡上对应题目的答案标号涂黑．）1．下列方程中是一元二次方程的是(    )A． B．  C． D． 2．下列图形中，是中心对称图形的是（    ）A．   B．   C．   D．  3．抛物线经过平移得到抛物线，平移过程正确的是（ 　　）A．先向左平移6个单位，再向上平移3个单位B．先向左平移6个单位，再向下平移3个单位C．先向右平移6个单位，再向上平移3个单位D．先向右平移6个单位，再向下平移3个单位4．的解为（　　）A． B． C． D．5．将抛物线向右平移2个单位长度，得到的抛物线为（    ）A． B． C． D．6．抛物线的顶点在（    ）A．第一象限 B．第二象限 C．第三象限 D．第四象限7．在抛物线上，当时，随的增大而增大，则的取值范围是（　　）A． B． C． D．8．关于x的函数是二次函数，则m的值为（    ）A．1 B． C．1或 D．09．如图中，，，点P从点A开始出发向点C以的速度移动，点Q从B点出发向点C以的速度移动，若P、Q分别同时从A，B出发，点P到点C后，P、Q都停止运动，(　　)秒后四边形是面积的．A．2 B．4.5 C．8 D．710．二次函数的图象如图所示，对称轴是直线．下列结论：①；②；③；④（为实数）．其中结论正确的为（    ）  A．①② B．②③④ C．①②④ D．①②③④11．某商品原价121元，连续两次降价后售价为100元，下列所列方程正确的是（　　）A． B．C． D．12．如图，点E为正方形内一点，，将绕点B按顺时针方向旋转，得到．延长交于点F，连接．下列结论：①；②四边形是正方形；③若，则；其中正确的是（    ）  A．①②③ B．①② C．②③ D．①二、填空题（本大题共6小题，每小题2分，共12分．）13．如图，老李想用长为的栅栏，再借助房屋的外墙（外墙长不超过）围成一个矩形羊圈，并在边上留一个宽的门（建在处，另用其他材料）．当羊圈的边为      m时，能围成一个面积为的羊圈．14．要组织一次足球联赛，赛制为双循环形式（每两队之间都进行两场比赛），共要比赛90场．设共有x个队参加比赛，列方程，并化成一般形式是           ．15．图（1）是一个横断面为抛物线形状的拱桥，当水面在1时，拱顶（拱桥洞的最高点）离水面2m，水面宽为4m．如果水面宽度为6m，则水面下降           ．  16．抛物线经过点，，则与的大小是           ．17．如图，将点绕原点顺时针旋转90°得到点，则点的坐标为           ．  18．如图，在矩形中，点P在边上，连接，将绕点P顺时针旋转90°得到，连接．若，，，则       ．   三、解答题（本大题共8小题，共72分．解答应写出文字说明、证明过程或演算步骤．）19．解方程：．20．如图网格中，的顶点均在格点上，点A、B的坐标分别是、．  (1)绕点O顺时针旋转后得到，在方格纸中画出，并写出点的坐标（______，______）；(2)点可以看成由点A经一次平移得到，平移距离为______；(3)在y轴上找一点P，使得最小，最小值为______．21．某水果商店推出一款水果拼盘套餐受到广大消费者的喜爱，每天销售量y盒与销售单价x元∕盒之间存在一次函数关系（如下表所示）．已知水果拼盘套餐的成本为30元∕盒．销售单价x元∕盒405060销售量y盒220200180(1)直接写出y与x的函数关系式：(2)当销售单价为多少时，当天的销售利润最大？(3)若水果商店希望通过调整，将这一款拼盘套餐降低成本m元∕盒，使每天在销售量不超过100盒的前提下，最大销售利润为7600元．求出m的值．22．武钢实验学校课外兴趣活动小组准备围建一个矩形花园．其中一边靠墙，另外三边用长为32米的篱笆围成，已知墙长16米（如图所示），设这个花园垂直于墙的一边长米．  (1)用含有x的式子表示，并写出x的取值范围；(2)若花园的面积为96平方米，求的长度．23．如图，点O是等边内一点，将绕点C按顺时针方向旋转得到，连接OD．  (1)求证：是等边三角形；(2)当，时，试判断的形状，并说明理由．24．某种服装，平均每天可销售20件，每件盈利44元，在每件降价幅度不超过10元的情况下，若每件降价1元，则每天可多售5件．设降价元．(1)每天的销量为_______件（用含的代数式表示）；(2)若每天获得1600元的利润，请你帮忙确定降价幅度；(3)该服装店能否通过降价销售的方式保证每天获得3000元的利润？并说明理由．25．某超市销售一种商品，成本价为20元/千克，经市场调查，每天销售量y（千克）与销售单价x（元/千克）之间的关系如图所示，规定每千克售价不能低于30元，且不高于80元．设每天的总利润为w元．  (1)根据图象求出y与x之间的函数关系式；(2)请求出w与x之间的函数关系式，当销售单价定为多少元时，该超市每天的利润最大？最大利润是多少元？(3)若该超市销售该商品所获利润不低于2800元，请直接写出x的取值范围．26．如图，在平面直角坐标系中，抛物线与x轴交于，两点，与y轴交于点．  (1)求该抛物线的函数表达式；(2)若点P是直线下方抛物线上的一动点，过点P作x轴的平行线交于点K，过点P作y轴的平行线交x轴于点D，求的最大值及此时点P的坐标；(3)在抛物线的对称轴上是否存在一点M，使得是以为腰的等腰三角形；若存在，请求出点M的坐标，若不存在，请说明理由．
参考答案：1．D【分析】根据一元二次方程的定义逐项分析即可判断．【详解】解：A、该方程中未知数的最高次数是1，不是一元二次方程，故本选项不符合题意；B、该方程中含两个有未知数．不是一元二次方程，故本选项不符合题意；C、该方程中分母中含有未知数．不属于整式方程，故本选项不符合题意； D、该方程符合一元二次方程的定义，故本选项符合题意；故选D．【点睛】本题考查一元二次方程的定义，掌握一元二次方程的定义是解题的关键．2．B【分析】根据中心对称图形的概念进行判断即可，根据把一个图形绕某一点旋转180度，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形，这个点叫做对称中心．【详解】解：A、不是中心对称图形，故该选项错误；B、是中心对称图形，故该选项正确；C、不是中心对称图形，故该选项错误；D、不是中心对称图形，故该选项错误；故选：B．【点睛】本题主要考查了中心对称图形，中心对称图形是要寻找对称中心，旋转180度后与自身重合．3．C【分析】直接根据“上加下减，左加右减”的原则进行解答即可．【详解】解：由“左加右减”的原则可知，将抛物线向右平移6个单位所得抛物线的解析式为：．由“上加下减”的原则可知，将抛物线向上平移3个单位所得抛物线的解析式为：；故选：C．【点睛】此题考查了二次函数图象的平移与几何变换，利用抛物线解析式的变化规律：左加右减，上加下减是解题关键．4．C【分析】根据因式分解法解方程即可．【详解】解：，，∴或，∴．故选C．【点睛】本题考查解一元二次方程．根据方程特点选择正确的方法求解是解题关键．5．D【分析】根据抛物线的平移规律：上加下减，左加右减解答即可．【详解】解：将抛物线向右平移2个单位得到的抛物线是，故选：D．【点睛】本题考查了二次函数图象的平移，掌握平移规律是解题的关键．6．A【分析】由抛物线的顶点式可以直接得到顶点坐标，即可求解．【详解】解：由题意得：抛物线的顶点坐标为：，在第一象限故选：A【点睛】本题考查抛物线的顶点式．掌握相关结论即可．7．C【分析】根据二次函数的性质判断即可．【详解】解：抛物线上，开口向上，对称轴为，在对称轴右侧，随的增大而增大，当时，随的增大而增大，，故选：C．【点睛】本题考查了二次函数的性质，由函数的增减性得到关于的不等式是解题的关键．8．B【分析】根据二次函数的定义求解即可．【详解】解：∵函数是二次函数，∴且，解得：．故选B．【点睛】本题考查二次函数的定义．一般地，我们把形如（其中是常数，）的函数叫做二次函数．9．A【分析】由于四边形是一个不规则的图形，不容易直接表示它的面积，观察图形，可知，因此当四边形是面积的时，是面积的，即有，从而列出关于t的方程求解即可．【详解】解：∵中，，，∴由勾股定理，得：．设t秒后四边形是面积的，则，．根据题意，知，∴，即，解得：，(舍去)．故选A．【点睛】本题考查了一元二次方程的应用，关键在于表示出三角形面积进而得出等量关系求解．10．D【分析】由抛物线开口方向，对称轴位置，抛物线与轴交点位置判断①，由与的关系及时可判断②，利用，根据时，时可判断③，由时取最小值可判断④．【详解】解抛物线开口向上，,抛物线对称轴为直线,抛物线与轴交点在轴下方,，故①正确．时, ,故②正确．,且，,，故③正确．时，为最小值，,故④正确．故选：D．【点睛】本题考查二次函数图象与系数的关系，解题关键是掌握二次函数的性质，掌握二次函数与方程及不等式的关系．11．B【分析】根据原价及经两次降价后的价格，即可得出关于a的一元二次方程，此题得解．【详解】解：根据题意可得，，故选：B．【点睛】本题考查了由实际问题抽象出一元二次方程，找准等量关系，正确列出一元二次方程是解题的关键．12．A【分析】设交于K，由及将绕点B按顺时针方向旋转，得到，可得，即可得，从而判断①正确；由旋转的性质可得，，，由正方形的判定可证四边形是正方形，可判断②正确；过点D作于H，由等腰三角形的性质可得，，由“”可得，可得，由旋转的性质可得，从而可得，判断③正确．【详解】解：设交于K，如图：   ∵四边形是正方形， ∴， ∴， ∵将绕点B按顺时针方向旋转，得到， ∴， ∵， ∴， ∴， ∴，故①正确； ∵将绕点B按顺时针方向旋转， ∴，，， 又∵， ∴四边形是矩形， 又∵， ∴四边形是正方形，故②正确； 如图，过点D作于H，  ∵，， ∴， ∴， ∵四边形是正方形， ∴，， ∴， ∴， 又∵，， ∴， ∴， ∵将绕点B按顺时针方向旋转， ∴， ∵四边形是正方形， ∴， ∴， ∴，故③正确； ∴正确的有：①②③， 故选：A．【点睛】本题是四边形综合题，考查了正方形的判定和性质，旋转的性质，全等三角形的判定和性质等知识，灵活运用这些性质进行推理是本题的关键．13．20【分析】设矩形的边，根据栅栏总长，再利用矩形面积公式即可求出．【详解】解：设矩形的边，则边；根据题意，得，化简，得，解得：，，当时，（不符合题意，舍去）；当时，．当羊圈的边为时，能围成一个面积为的羊圈．故答案为：20．【点睛】本题考查了一元二次方程的应用，解题的关键是要理解题意，能正确列出方程．14．【分析】设共有x个队参加比赛，根据每两队之间都进行两场比赛，共要比赛90场，可列出方程．【详解】解：共有x个队参加比赛，根据题意得：，即．故答案为：【点睛】本题考查了由实际问题抽象出一元二次方程，解题的关键是理解题意，找准等量关系，列出方程．15．米/【分析】由图中可以看出，所求抛物线的顶点在原点，对称轴为轴，可设此函数解析式为：，利用待定系数法求出解析式，再根据水面宽度为6m时，求出当时，对应y值即可解答．【详解】解：设此函数解析式为：，；则应在此函数解析式上．则即得，∴．当时，∴水面下降（米）故答案为：米．【点睛】本题考查了二次函数的实际应用，根据题意得到函数解析式的表示方法是解决本题的关键，关键在于找到在此函数解析式上的点．16．【分析】根据抛物线开口向下，当时，随的增大而减小，即可求解．【详解】解：∵，，对称轴为直线，∴当时，随的增大而减小，∵抛物线经过点，，，∴，故答案为：．【点睛】本题考查了二次函数的性质，熟练掌握二次函数的性质是解题的关键．17．【分析】过点、分别作轴的垂线，垂足为、，则，由旋转的性质和角之间的关系可证，，，即可得到点的坐标．【详解】如图，过点、两点分别作轴的垂线，垂足为、，则，  点，，，线段绕点顺时针旋转，，，，，，在与中，，∴，，，点．故答案为：．【点睛】本题考查了点的坐标与旋转变换的关系．关键是根据旋转的性质和角之间的关系确定全等三角形．18．2【分析】过点作于点F，则，可证，于是．设，，，解得，于是．【详解】解：过点作于点F，则，∵，∴．又，∴.∴．设，矩形中，，，，，解得，∴．故答案为：2  【点睛】本题考查矩形的性质，全等三角形的判定和性质，勾股定理；根据勾股定理构建方程求解是解题的关键．19．，【分析】运用公式法求解一元二次方程；【详解】解：，∴，，，，，∴，．【点睛】本题考查一元二次方程的求解；掌握求根公式是解题的关键．20．(1)图见解析，3，(2)(3) 【分析】（1）根据旋转的性质，画出，再写出的坐标即可；（2）根据平移规则，结合勾股定理进行求解即可；（3）利用将军饮马模型，作出点即可．【详解】（1）解：如图，即为所求，  点的坐标，故答案为：3，．（2）如图，由勾股定理，得：；（3）如图，点P即为所求作，最小值为．【点睛】本题考查坐标与图形变换，熟练掌握旋转，平移，轴对称的性质，是解题的关键．21．(1)(2)90元∕盒(3)6 【分析】（1）根据待定系数法解答即可；（2）设销售单价x（元/盒）时，每天的销售利润为w元，根据每天销售利润=每件的利润×销售量即可得出w关于x的二次函数，然后根据二次函数的性质即可求出结果；（3）先由每天销售量不得超过100件求出x的取值范围，然后根据每天销售利润=每件的利润×销售量列出w关于x的二次函数（含m），然后根据二次函数的性质即可得到w的最大值，进而可得关于m的方程，解方程即得结果．【详解】（1）解：设y与x的函数关系式为，根据题意，得，解得，∴（2）解：设销售单价x（元/盒）时，每天的销售利润为w元，根据题意，得，∴当元时，w有最大值，最大值为7200，即销售单价为90元∕盒时，当天的销售利润最大；（3）解：由题意可列出不等式组：，解得：，∴，∴该二次函数的图象开口向下且对称轴为直线：，∵，∴，又∵，∴当时，w有最大值为，又∵w有最大值为7600，∴，解得：．∴m的值为6．【点睛】本题考查了二次函数的应用，属于常考题型，正确理解题意、列出函数关系式、熟练掌握二次函数的性质是解题的关键．22．(1)，(2)的长度为12米 【分析】（1）由篱笆长32米即可得出用含有x的式子表示的式子，再根据、、即可求出自变量的取值范围；（2）根据矩形的面积公式，即可得出关于x的一元二次方程，解之即可得出x的值，再由（1）中x的取值范围即可确定x的值．【详解】（1）∵，米，∴．∵，∴；（2）根据题意得：，解得： （不合题意，舍去）．答：若苗圃园的面积为96平方米，则的长度为12米．【点睛】本题考查了一元二次方程的应用、矩形的面积，解题的关键是：（1）根据篱笆长度得出用含有x的式子表示的式子；（2）利用矩形的面积公式，找出关于x的一元二次方程．23．(1)见解析(2)等腰直角三角形，理由见解析 【分析】（1）利用有一个角为的等腰三角形为等边三角形即可得证；（2）三角形为等腰直角三角形，理由为：由旋转得到两三角形全等，进而求出，再由三角形为等边三角形， 进而确定出为直角，即可得证 ．【详解】（1）证明：∵绕点C按顺时针方向旋转得到∴，∴，∵，∴是等边三角形；（2）解：是等腰直角三角形，理由如下：∵是等边三角形，∵，∴，∴∵，∴，∴，∴，∴是等腰直角三角形．【点睛】此题考查了旋转的性质，以及等边三角形的判定与性质，熟练掌握旋转的性质是解本题的关键．24．(1)(2)降价幅度为4元(3)不能，理由见解析 【分析】（1）利用每天的销售量每件降低的价格，可用含的代数式表示出每天的销售量；（2）利用每天销售该服装获得的总利润每件的销售利润每天的销售量，即可得出关于的一元二次方程，解之即可得出的值，再结台每件降价幅度不超过元，即可得出每件服装应降价元；（3）列一元二次方程求解，根据一元二次方程无解即可判断．【详解】（1）解：依题意得，每天可以销售件服装．故答案为∶；（2）解：根据题意，得，解得，（不符合题意，舍去），所以降价幅度为元；（3）解：不能，理由如下，根据题意，得，整理，得，∴，所以原方程无解，因此该服装店不能通过降价销售的方式保证每天获得元的利润．【点睛】本题考查了一元二次方程的应用以及列代数式，找准等量关系，正确列出一元二次方程是解题的关键．25．(1)(2)；80元； 6000元(3) 【分析】（1）设与之间的函数关系式为，由待定系数法求解即可；（2）利用总利润等于每千克的利润乘以销售量列出函数关系，将关于的二次函数写成顶点式，根据二次函数的性质及自变量的取值范围可得答案．（3）当时，得或，根据二次函数的性质和题目中x满足的条件综合得出x的取值范围．【详解】（1）解：设与之间的函数关系式为，将；分别代入得：，解得：，与之间的函数关系式为；（2）由题意得：，；，，抛物线开口向下，对称轴为直线，当时，随的增大而增大，当时，有最大值，此时，当销售单价定为80元时，该超市每天的利润最大，最大利润是6000元．（3），当时，，解得，或，抛物线开口向下时，，【点睛】本题考查了二次函数与一次函数在销售问题中的应用，理清题中的数量关系并熟练掌握二次函数的性质是解题的关键．26．(1)(2)存在，的最大值为，(3)存在，的坐标为或或或． 【分析】（1）将、、代入抛物线解析式求解即可；（2）可求直线的解析式为，设（），可求，从而可求，即可求解；（3）设，可求，，分和，两种情况讨论，列出一元二次方程，即可求解．【详解】（1）解：由题意得 ，解得：，∴抛物线的解析式为．（2）解：设直线的解析式为，则有，解得：，∴直线的解析式为；设（），，解得：，，，，，，，∴当时，的最大值为，，．故的最大值为，．（3）解：存在，∵抛物线的对称轴为直线，设，，，，当，即时， ，解得：，∴点M的坐标为或；当，即时，，解得：，∴点M的坐标为或；综上所述：存在，的坐标为或或或．【点睛】本题考查了待定系数法求函数解析式，二次函数中动点最值问题，等腰三角形的判定，勾股定理等，掌握解法及找出动点坐标满足的函数解析式是解题的关键．