2024年高考数学第一轮复习38_专题十一115变量间的相关关系、统计案例（专题试卷+讲解PPT）

这是一份2024年高考数学第一轮复习38_专题十一115变量间的相关关系、统计案例（专题试卷+讲解PPT），文件包含1_115变量间的相关关系统计案例分层集训pptx、1_115变量间的相关关系统计案例pptx、1_115变量间的相关关系统计案例docx、1_115变量间的相关关系统计案例十年高考docx等4份课件配套教学资源，其中PPT共75页， 欢迎下载使用。
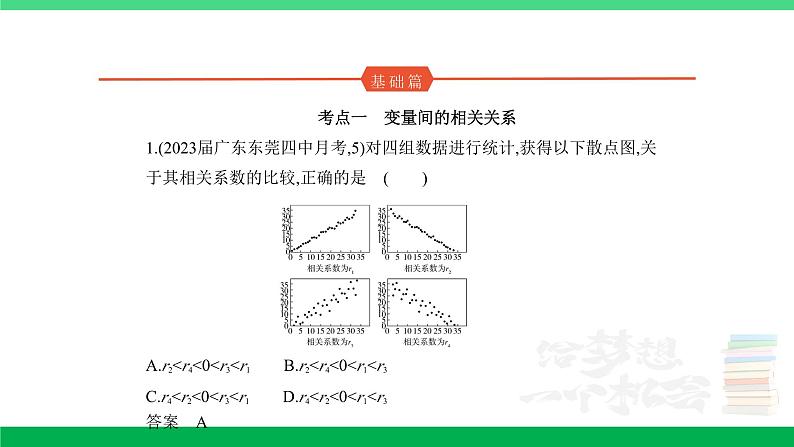
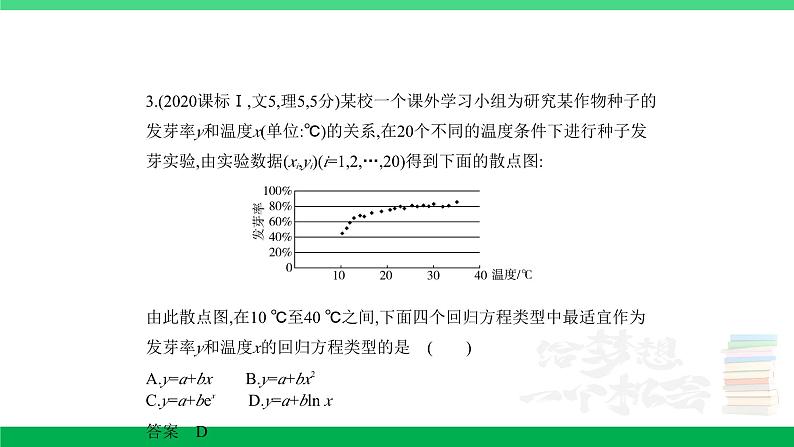
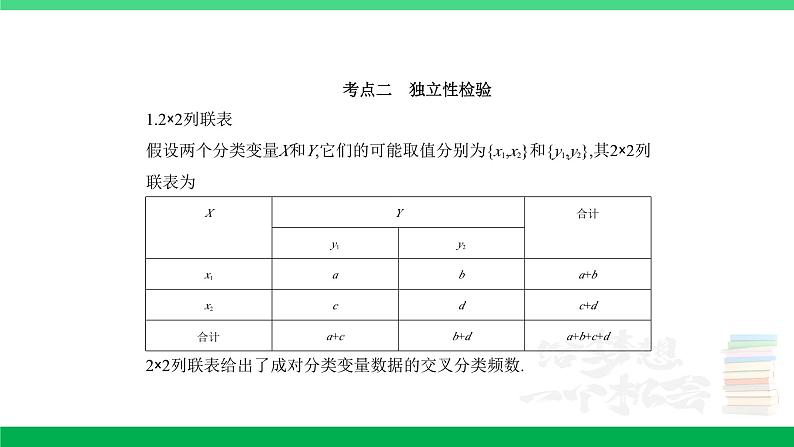
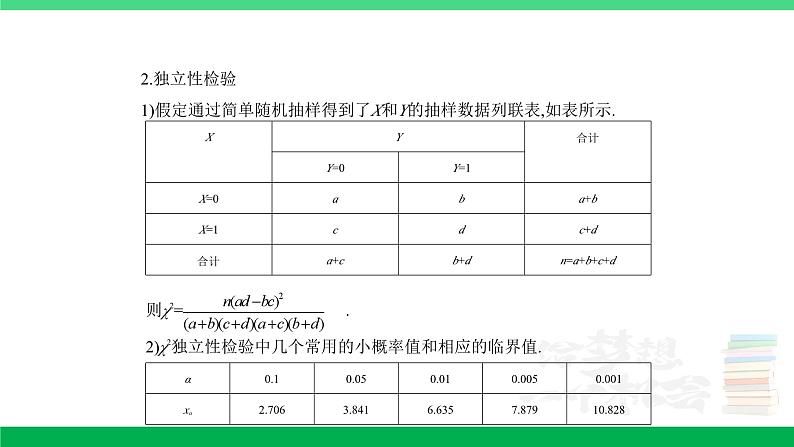
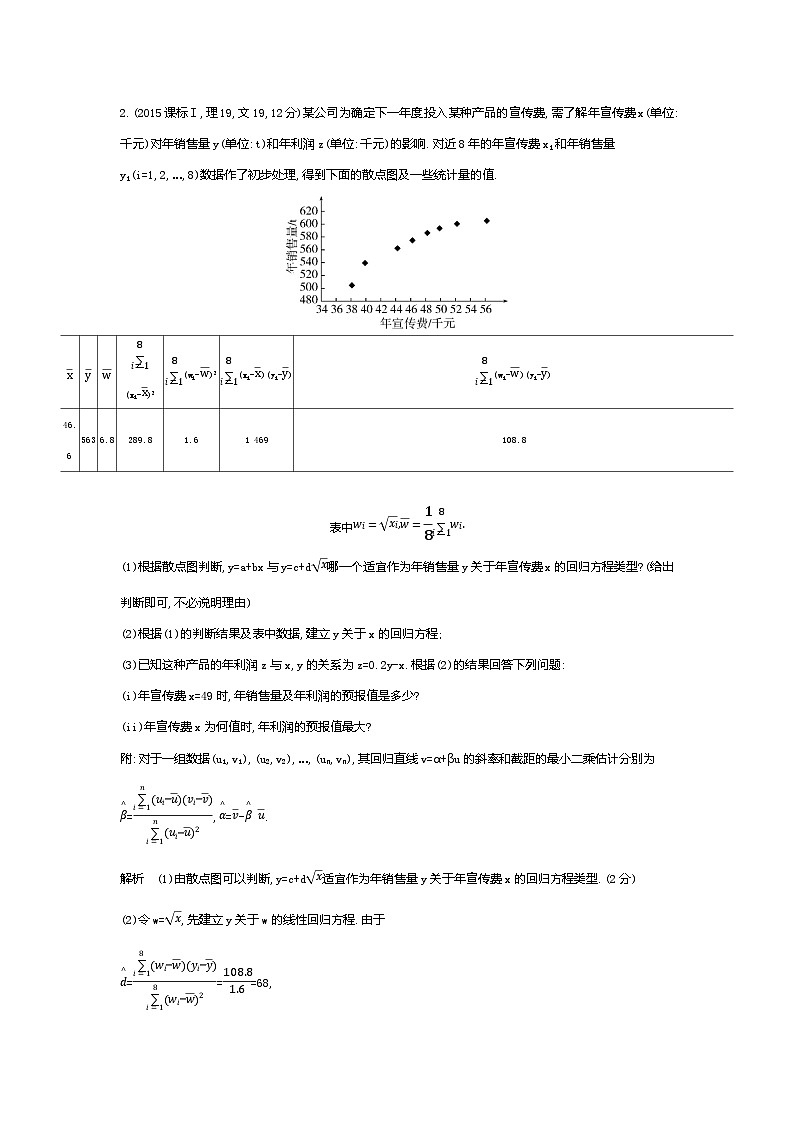
11.5　变量间的相关关系、统计案例 考点一　变量间的相关关系   (2020课标Ⅱ理,18,12分)某沙漠地区经过治理,生态系统得到很大改善,野生动物数量有所增加.为调查该地区某种野生动物的数量,将其分成面积相近的200个地块,从这些地块中用简单随机抽样的方法抽取20个作为样区,调查得到样本数据(xi,yi)(i=1,2,…,20),其中xi和yi分别表示第i个样区的植物覆盖面积(单位:公顷)和这种野生动物的数量,并计算得xi=60,yi=1 200,(xi-)2=80,(yi-)2=9 000,(xi-)(yi-)=800.(1)求该地区这种野生动物数量的估计值(这种野生动物数量的估计值等于样区这种野生动物数量的平均数乘以地块数);(2)求样本(xi,yi)(i=1,2,…,20)的相关系数(精确到0.01);(3)根据现有统计资料,各地块间植物覆盖面积差异很大.为提高样本的代表性以获得该地区这种野生动物数量更准确的估计,请给出一种你认为更合理的抽样方法,并说明理由.附:相关系数=,≈1.414.解析　(1)由已知得样本平均数yi=60,从而该地区这种野生动物数量的估计值为60×200=12 000.(2)样本(xi,yi)(i=1,2,…,20)的相关系数≈0.94.(3)分层抽样:根据植物覆盖面积的大小对地块分层,再对200个地块进行分层抽样.理由如下:由(2)知各样区的这种野生动物数量与植物覆盖面积有很强的正相关.由于各地块间植物覆盖面积差异很大,从而各地块间这种野生动物数量差异也很大,采用分层抽样的方法较好地保持了样本结构与总体结构的一致性,提高了样本的代表性,从而可以获得该地区这种野生动物数量更准确的估计. 2.(2015课标Ⅰ,理19,文19,12分)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响.对近8年的年宣传费xi和年销售量yi(i=1,2,…,8)数据作了初步处理,得到下面的散点图及一些统计量的值.(xi-)2(wi-)2(xi-)(yi-)(wi-)(yi-)46.65636.8289.81.61 469108.8 (1)根据散点图判断,y=a+bx与y=c+d哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)(2)根据(1)的判断结果及表中数据,建立y关于x的回归方程;(3)已知这种产品的年利润z与x,y的关系为z=0.2y-x.根据(2)的结果回答下列问题:(i)年宣传费x=49时,年销售量及年利润的预报值是多少?(ii)年宣传费x为何值时,年利润的预报值最大?附:对于一组数据(u1,v1),(u2,v2),…,(un,vn),其回归直线v=α+βu的斜率和截距的最小二乘估计分别为=,=- .解析　(1)由散点图可以判断,y=c+d适宜作为年销售量y关于年宣传费x的回归方程类型.(2分)(2)令w=,先建立y关于w的线性回归方程.由于===68,=- =563-68×6.8=100.6,所以y关于w的线性回归方程为=100.6+68w,因此y关于x的回归方程为=100.6+68.(6分)(3)(i)由(2)知,当x=49时,年销售量y的预报值=100.6+68=576.6,年利润z的预报值=576.6×0.2-49=66.32.(9分)(ii)根据(2)的结果知,年利润z的预报值=0.2(100.6+68)-x=-x+13.6+20.12.所以当==6.8,即x=46.24时,取得最大值.故年宣传费为46.24千元时,年利润的预报值最大.(12分)3.(2015重庆文,17,13分)随着我国经济的发展,居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款(年底余额)如下表:年份20102011201220132014时间代号t12345储蓄存款y(千亿元)567810 (1)求y关于t的回归方程=t+;(2)用所求回归方程预测该地区2015年(t=6)的人民币储蓄存款.附:回归方程=t+中,==-.解析　(1)列表计算如下:itiyitiyi11515226412337921448163255102550153655120 这里n=5,=ti==3,=yi==7.2.又ltt=-n=55-5×32=10,lty=tiyi-n　=120-5×3×7.2=12,从而===1.2,=-=7.2-1.2×3=3.6,故所求回归方程为=1.2t+3.6.(2)将t=6代入回归方程可预测该地区2015年的人民币储蓄存款为=1.2×6+3.6=10.8(千亿元).4.(2014课标Ⅱ理,19,12分)某地区2007年至2013年农村居民家庭人均纯收入y(单位:千元)的数据如下表:年　份2007200820092010201120122013年份代号t1234567人均纯收入y2.93.33.64.44.85.25.9 (1)求y关于t的线性回归方程;(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.附:回归直线的斜率和截距的最小二乘估计公式分别为:=,=-.解析　(1)由所给数据计算得=×(1+2+3+4+5+6+7)=4,=×(2.9+3.3+3.6+4.4+4.8+5.2+5.9)=4.3,(ti-)2=9+4+1+0+1+4+9=28,(ti-)(yi-)=(-3)×(-1.4)+(-2)×(-1)+(-1)×(-0.7)+0×0.1+1×0.5+2×0.9+3×1.6=14,===0.5,=-=4.3-0.5×4=2.3,所求回归方程为=0.5t+2.3.(2)由(1)知,=0.5>0,故2007年至2013年该地区农村居民家庭人均纯收入逐年增加,平均每年增加0.5千元.将2015年的年份代号t=9代入(1)中的回归方程,得=0.5×9+2.3=6.8,故预测该地区2015年农村居民家庭人均纯收入为6.8千元.评析　本题考查了回归直线方程的求解,注意回归直线恒过点(,)是关键,考查了回归系数的几何意义.考查了学生的计算求解能力.考点二　独立性检验1.(2021全国甲理,17,12分)甲、乙两台机床生产同种产品,产品按质量分为一级品和二级品,为了比较两台机床产品的质量,分别用两台机床各生产了200件产品,产品的质量情况统计如下表: 一级品二级品合计甲机床15050200乙机床12080200合计270130400(1)甲机床、乙机床生产的产品中一级品的频率分别是多少?(2)能否有99%的把握认为甲机床的产品质量与乙机床的产品质量有差异?附:K2=,P(K2≥k)0.0500.0100.001k3.8416.63510.828.解析　(1)因为甲机床生产的200件产品中有150件一级品,所以甲机床生产的产品中一级品的频率为,因为乙机床生产的200件产品中有120件一级品,所以乙机床生产的产品中一级品的频率为.(2)根据2×2列联表中的数据,得K2==≈10.256,因为10.256>6.635,所以有99%的把握认为甲机床的产品质量与乙机床的产品质量有差异.方法总结　解决独立性检验问题的一般步骤:2.(2020新高考Ⅰ,19,12分)为加强环境保护,治理空气污染,环境监测部门对某市空气质量进行调研,随机抽查了100天空气中的PM2.5和SO2浓度(单位:μg/m3),得下表:
 　　　SO2 PM2.5　　　 [0,50](50,150](150,475][0,35]32184(35,75]6812(75,115]3710(1)估计事件“该市一天空气中PM2.5浓度不超过75,且SO2浓度不超过150”的概率;(2)根据所给数据,完成下面的2×2列联表:　　　SO2PM2.5　　　 [0,150](150,475][0,75]  (75,115]  (3)根据(2)中的列联表,判断是否有99%的把握认为该市一天空气中PM2.5浓度与SO2浓度有关.附:K2=,P(K2≥k)0.0500.0100.001k3.8416.63510.828.　解析(1)根据抽查数据,该市100天的空气中PM2.5浓度不超过75,且SO2浓度不超过150的天数为32+18+6+8=64,因此,该市一天空气中PM2.5浓度不超过75,且SO2浓度不超过150的概率的估计值为=0.64.              (4分)(2)根据抽查数据,可得2×2列联表:　　SO2PM2.5　　 [0,150](150,475][0,75]6416(75,115]1010(8分)(3)根据(2)的列联表得K2=≈7.484.由于7.484>6.635,故有99%的把握认为该市一天空气中PM2.5浓度与SO2浓度有关. (12分)3.(2022全国甲文,17,12分,应用性)甲、乙两城之间的长途客车均由A和B两家公司运营.为了解这两家公司长途客车的运行情况,随机调查了甲、乙两城之间的500个班次,得到下面列联表: 准点班次数未准点班次数A24020B21030(1)根据上表,分别估计这两家公司甲、乙两城之间的长途客车准点的概率;(2)能否有90%的把握认为甲、乙两城之间的长途客车是否准点与客车所属公司有关?附:K2=,P(K2≥k)0.1000.0500.010k2.7063.8416.635解析　(1)由题意可得A公司长途客车准点的概率P1=,B公司长途客车准点的概率P2=.(2)因为K2=≈3.205>2.706,所以有90%的把握认为甲、乙两城之间的长途客车是否准点与客车所属公司有关.