2024年高考数学第一轮复习5_专题三31函数及其性质（专题试卷+讲解PPT）

这是一份2024年高考数学第一轮复习5_专题三31函数及其性质（专题试卷+讲解PPT），文件包含1_31函数及其性质分层集训pptx、1_31函数及其性质pptx、1_31函数及其性质docx、1_31函数的概念及表示十年高考docx等4份课件配套教学资源，其中PPT共96页， 欢迎下载使用。
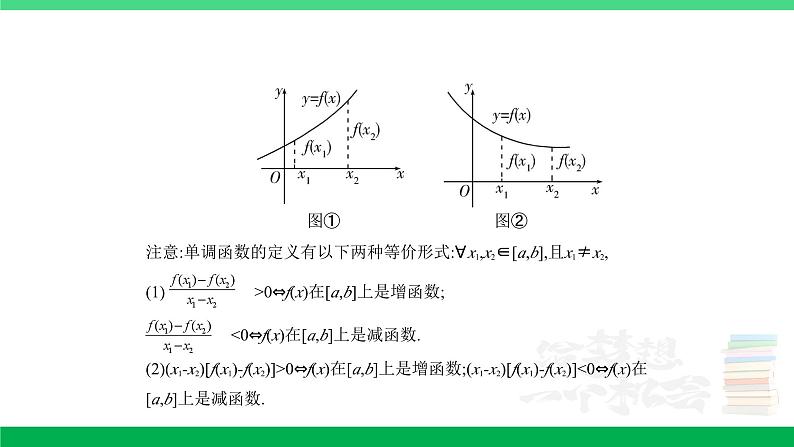
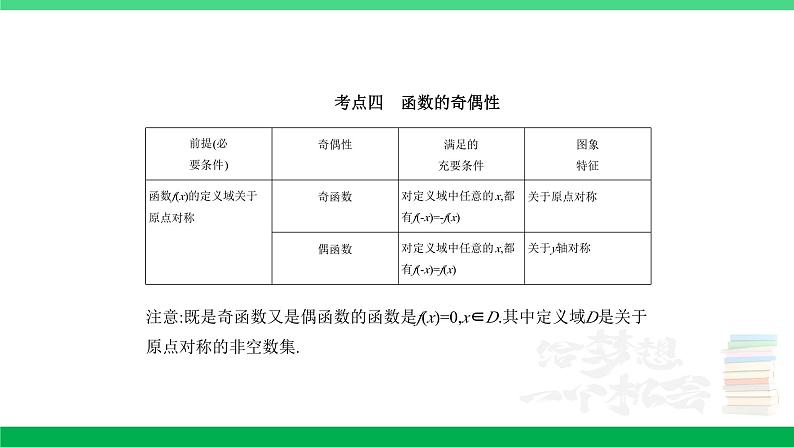
专题三　函数的概念与基本初等函数3.1　函数及其性质考点一　函数的概念及表示1.(2015湖北文,7,5分)设x∈R,定义符号函数sgn x=则(　　)A.|x|=x|sgn x|　　　　　B.|x|=xsgn|x|C.|x|=|x|sgn x　　　　　D.|x|=xsgn x答案　D　由已知可知xsgn x=而|x|=所以|x|=xsgn x,故选D.2.(2014江西理,3,5分)已知函数f(x)=5|x|,g(x)=ax2-x(a∈R).若f[g(1)]=1,则a=(　　)A.1　　　B.2　　　C.3　　　D.-1答案　A　由已知条件可知: f[g(1)]=f(a-1)=5|a-1|=1,∴|a-1|=0,得a=1.故选A.评析　本题主要考查函数的解析式,正确理解函数的定义是解题关键.3.(2017山东理,1,5分)设函数y=的定义域为A,函数y=ln(1-x)的定义域为B,则A∩B=(　　)A.(1,2)　　　　　B.(1,2]C.(-2,1)　　　　　D.[-2,1)答案　D　由4-x2≥0,解得-2≤x≤2,由1-x>0,解得x<1,∴A∩B={x|-2≤x<1}.故选D.4.(2015重庆文,3,5分)函数f(x)=log2(x2+2x-3)的定义域是(　　)A.[-3,1]B.(-3,1)C.(-∞,-3]∪[1,+∞)D.(-∞,-3)∪(1,+∞)答案　D　由x2+2x-3>0,解得x<-3或x>1,故选D.5.(2015湖北文,6,5分)函数f(x)=+lg的定义域为(　　)A.(2,3)　　　　　B.(2,4]C.(2,3)∪(3,4]　　　　　D.(-1,3)∪(3,6]答案　C　要使函数f(x)有意义,需满足即解之得2<x<3或3<x≤4,故选C.6.(2014山东理,3,5分)函数f(x)=的定义域为(　　)A.　　　　　B.(2,+∞)C.∪(2,+∞)　　　　　D.∪[2,+∞)答案　C　要使函数f(x)有意义,需使(log2x)2-1>0,即(log2x)2>1,∴log2x>1或log2x<-1.解之得x>2或0<x<.故f(x)的定义域为∪(2,+∞).7.(2016课标Ⅱ文,10,5分)下列函数中,其定义域和值域分别与函数y=10lg x的定义域和值域相同的是(　　)A.y=x　　　B.y=lg x　　　C.y=2x　　　D.y=答案　D　函数y=10lg x的定义域、值域均为(0,+∞),而y=x,y=2x的定义域均为R,排除A,C;y=lg x的值域为R,排除B,故选D.易错警示　利用对数恒等式将函数y=10lg x变为y=x,将其值域认为是R是失分的主要原因.评析　本题考查函数的定义域和值域,熟练掌握基本初等函数的图象和性质是解题的关键.8.(2022北京,4,4分)已知函数f(x)=,则对任意实数x,有 (　　)A. f(-x)+f(x)=0　　　　B. f(-x)-f(x)=0C. f(-x)+f(x)=1　　　　D. f(-x)-f(x)=答案　C　∵f(x)=,∴f(-x)=,∴f(x)+f(-x)==1.故选C.一题多解:若对任意实数x,使得选项中式子成立,则可任取x值,代入验证,进行排除.当x=0时, f(0)+f(0)==1, f(0)-f(0)=0,故A,D选项错误.当x=1时, f(-1)-f(1)=≠0,故B选项错误.根据排除法可知选C.9.(2022北京,11,5分)函数f(x)=的定义域是　　　　　　. 答案　(-∞,0)∪(0,1]解析　由题意得解得x≤1且x≠0,所以函数f(x)的定义域为(-∞,0)∪(0,1]. 10.(2015课标Ⅱ文,13,5分)已知函数f(x)=ax3-2x的图象过点(-1,4),则a=　　　　. 答案　-2解析　因为函数f(x)=ax3-2x的图象过点(-1,4),所以4=a×(-1)3-2×(-1),故a=-2.11.(2016江苏,5,5分)函数y=的定义域是　　　　. 答案　[-3,1]解析　若函数有意义,则3-2x-x2≥0,即x2+2x-3≤0,解得-3≤x≤1.考点二　分段函数1.(2015陕西文,4,5分)设f(x)=则f(f(-2))=(　　)A.-1　　　B.　　　C.　　　D.答案　C　∵f(-2)=2-2=,∴f(f(-2))=f =1-=,选C.2.(2015山东文,10,5分)设函数f(x)=若f =4,则b=(　　)A.1　　　B.　　　C.　　　D.答案　D　f=3×-b=-b,当-b≥1,即b≤时,f=,即=4=22,得到-b=2,即b=;当-b<1,即b>时,f=-3b-b=-4b,即-4b=4,得到b=<,舍去.综上,b=,故选D.3.(2014江西文,4,5分)已知函数f(x)=(a∈R),若f [f(-1)]=1,则a=(　　)A.　　　B.　　　C.1　　　D.2答案　A　由f[f(-1)]=f(2)=4a=1,得a=,故选A.4.(2022浙江,14,6分)已知函数f(x)=则f=　　　　;若当x∈[a,b]时,1≤f(x)≤3,则b-a的最大值是　　　　. 答案　 ;3+解析　∵f,∴f.f(x)的大致图象如图.∵当x∈[a,b]时,1≤f(x)≤3,∴由图可得b>1且b+-1=3,∴b=2+,∵f(a)=1,∴-a2+2=1,解得a=1或a=-1,∴(b-a)max=2+-(-1)=3+.一题多解:第二空:∵当x≤1时,y=-x2+2≤2,∴f(x)=3⇒x+-1=3(x>1),故x=2+,令-x2+2=1(x≤1),解得x=1或x=-1,令x+-1=1(x>1),无解,∴amin=-1,b=2+,∴(b-a)max=2+-(-1)=3+.5.(2014课标Ⅰ文,15,5分)设函数f(x)=则使得f(x)≤2成立的x的取值范围是　　　　. 答案　(-∞,8]解析　f(x)≤2⇒或⇒或⇒x<1或1≤x≤8⇒x≤8,故填(-∞,8].考点三 函数的单调性与最值1.(2021全国甲文,4,5分)下列函数中是增函数的为 (　　)A. f(x)=-x　　　　B. f(x)=C. f(x)=x2　　　　D. f(x)=答案　D　解题指导:排除法,利用基本初等函数的性质逐一判断四个选项.解析　对于f(x)=-x,由正比例函数的性质可知, f(x)是减函数,故A不符合题意;对于f(x)=,由指数函数的单调性可知, f(x)是减函数,故B不符合题意;对于f(x)=x2,由二次函数的图象可知, f(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增,故C不符合题意;对于f(x)=,由幂函数的性质可知, f(x)在(-∞,+∞)上单调递增,故选D.方法总结:一次函数y=kx+b(k≠0)单调性的判断:若k>0,则函数在R上单调递增;若k<0,则函数在R上单调递减.指数函数y=ax(a>0且a≠1)单调性的判断:若a>1,则函数在R上单调递增;若0<a<1,则函数在R上单调递减.幂函数y=xα单调性的判断:若α>0,则函数在(0,+∞)上单调递增;若α<0,则函数在(0,+∞)上单调递减.2.(2021全国乙文,8,5分)下列函数中最小值为4的是 (　　)A.y=x2+2x+4　　　　B.y=|sin x|+C.y=2x+22-x　　　　D.y=ln x+答案　C　解题指导:对于A,利用配方法或二次函数的单调性求最值,对于B,C,D,利用换元法转化为对勾函数进行判断.解析　对于A,y=x2+2x+4=(x+1)2+3≥3,所以它的最小值为3,所以A不符合题意;对于B,设|sin x|=t,则0<t≤1,y=|sin x|+,t∈(0,1],易知y=t+在(0,1]上单调递减,故t=1时,ymin=1+=5,所以B不符合题意;对于C,令2x=t(t>0),则y=2x+22-x=t+,t>0,易知y=t+在(0,2)上单调递减,在(2,+∞)上单调递增,所以当t=2时,y取最小值,ymin=2+=4,故C符合题意;对于D,令ln x=t,t∈R且t≠0,则y=ln x+,显然t<0时,函数值小于0,不符合题意.故选C.3.(2020新高考Ⅰ,8,5分)若定义在R的奇函数f(x)在(-∞,0)单调递减,且f(2)=0,则满足xf(x-1)≥0的x的取值范围是              (　　)A.[-1,1]∪[3,+∞)　　　　B.[-3,-1]∪[0,1]C.[-1,0]∪[1,+∞)　　　　D.[-1,0]∪[1,3]答案　D　∵f(x)是定义在R上的奇函数,∴f(x-1)的图象关于点(1,0)中心对称,又∵f(x)在(-∞,0)上单调递减,∴f(x-1)在(-∞,1)上单调递减,在(1,+∞)上也单调递减,且过(-1,0)和(3,0),f(x-1)的大致图象如图:当-1≤x≤0时,f(x-1)≤0,∴xf(x-1)≥0;当1≤x≤3时,f(x-1)≥0,∴xf(x-1)≥0.综上,满足xf(x-1)≥0的x的取值范围是[-1,0]∪[1,3].故选D. 4.(2019北京文,3,5分)下列函数中,在区间(0,+∞)上单调递增的是(　　)A.y=　　　　　B.y=2-xC.y=lox　　　　　D.y=答案　A　本题主要考查指数函数、对数函数、幂函数的单调性,考查数形结合的思想.考查的核心素养是直观想象.A选项,>0,所以幂函数y=在(0,+∞)上单调递增.B选项,指数函数y=2-x=在(0,+∞)上单调递减.C选项,因为0<<1,所以对数函数y=lox在(0,+∞)上单调递减.D选项,反比例函数y=在(0,+∞)上单调递减.解题关键　熟练掌握基本初等函数的图象和性质是解决本题的关键.5.(2016北京文,4,5分)下列函数中,在区间(-1,1)上为减函数的是(　　)A.y=　　　　　B.y=cos xC.y=ln(x+1)　　　　　D.y=2-x答案　D　选项A中,y==的图象是将y=-的图象向右平移1个单位得到的,故y=在(-1,1)上为增函数,不符合题意;选项B中,y=cos x在(-1,0)上为增函数,在(0,1)上为减函数,不符合题意;选项C中,y=ln(x+1)的图象是将y=ln x的图象向左平移1个单位得到的,故y=ln(x+1)在(-1,1)上为增函数,不符合题意;选项D符合题意.评析　本题考查了基本函数的图象和性质以及图象的变换,属中档题.6.(2015课标Ⅱ文,12,5分)设函数f(x)=ln(1+|x|)-,则使得f(x)>f(2x-1)成立的x的取值范围是(　　)A.B.∪(1,+∞)C.D.∪答案　A　当x>0时,f(x)=ln(1+x)-,∴f '(x)=+>0,∴f(x)在(0,+∞)上为增函数,∵f(-x)=f(x),∴f(x)为偶函数,由f(x)>f(2x-1)得f(|x|)>f(|2x-1|),∴|x|>|2x-1|,即3x2-4x+1<0,解得<x<1,故选A.7.(2016浙江,7,5分)已知函数f(x)满足:f(x)≥|x|且f(x)≥2x,x∈R.(　　)A.若f(a)≤|b|,则a≤bB.若f(a)≤2b,则a≤bC.若f(a)≥|b|,则a≥bD.若f(a)≥2b,则a≥b答案　B　依题意得f(a)≥2a,若f(a)≤2b,则2a≤f(a)≤2b,∴2a≤2b,又y=2x是R上的增函数,∴a≤b.故选B.8.(2016北京文,10,5分)函数f(x)=(x≥2)的最大值为　　　　. 答案　2解析　解法一:∵f '(x)=,∴x≥2时, f '(x)<0恒成立,∴f(x)在[2,+∞)上单调递减,∴f(x)在[2,+∞)上的最大值为f(2)=2.解法二:∵f(x)===1+,∴f(x)的图象是将y=的图象向右平移1个单位,再向上平移1个单位得到的.∵y=在[2,+∞)上单调递减,∴f(x)在[2,+∞)上单调递减,故f(x)在[2,+∞)上的最大值为f(2)=2.解法三:由题意可得 f(x)=1+.∵x≥2,∴x-1≥1,∴0<≤1,∴1<1+≤2,即1<≤2.故f(x)在[2,+∞)上的最大值为2.评析　本题考查函数的最值,有多种解法,属中档题.9.(2015浙江文,12,6分)已知函数f(x)=则f(f(-2))=　　　　, f(x)的最小值是　　　　. 答案　-;2-6解析　f(-2)=(-2)2=4,f(f(-2))=f(4)=4+-6=-.当x≤1时, f(x)=x2≥0,当x>1时,f(x)=x+-6≥2-6,当且仅当x=时,等号成立,又2-6<0,所以f(x)min=2-6.10.(2016天津,13,5分)已知f(x)是定义在R上的偶函数,且在区间(-∞,0)上单调递增.若实数a满足f(2|a-1|)>f(-),则a的取值范围是　　　　. 答案　解析　由题意知函数f(x)在(0,+∞)上单调递减.因为f(2|a-1|)>f(-), f(-)=f(),所以f(2|a-1|)>f(),所以2|a-1|<,解之得<a<.考点四　函数的奇偶性1.(2015北京文,3,5分)下列函数中为偶函数的是(　　)A.y=x2sin x　　　　　B.y=x2cos xC.y=|ln x|　　　　　D.y=2-x答案　B　A中函数为奇函数,B中函数为偶函数,C与D中函数均为非奇非偶函数,故选B.2.(2014课标Ⅰ,理3,文5,5分)设函数f(x),g(x)的定义域都为R,且f(x)是奇函数,g(x)是偶函数,则下列结论中正确的是(　　)A.f(x)g(x)是偶函数B.|f(x)|g(x)是奇函数C.f(x)|g(x)|是奇函数D.|f(x)g(x)|是奇函数答案　C　由题意可知 f(-x)=-f(x),g(-x)=g(x),对于选项A, f(-x)·g(-x)=-f(x)·g(x),所以f(x)g(x)是奇函数,故A项错误;对于选项B,|f(-x)|g(-x)=|-f(x)|g(x)=|f(x)|g(x),所以|f(x)|g(x)是偶函数,故B项错误;对于选项C, f(-x)|g(-x)|=-f(x)|g(x)|,所以f(x)|g(x)|是奇函数,故C项正确;对于选项D,|f(-x)g(-x)|=|-f(x)g(x)|=|f(x)g(x)|,所以|f(x)g(x)|是偶函数,故D项错误,选C.评析　本题考查函数奇偶性的定义及其应用,考查学生的知识应用能力及逻辑推理论证能力,准确理解函数奇偶性的定义是解决本题的关键.3.(2011课标,理2,文3,5分)下列函数中,既是偶函数又在(0,+∞)单调递增的函数是(　　)A.y=x3　　　　　B.y=|x|+1C.y=-x2+1　　　　　D.y=2-|x|答案　B　y=x3是奇函数,y=-x2+1和y=2-|x|在(0,+∞)上都是减函数,故选B.评析　本题考查函数的奇偶性和单调性的判定,属容易题.4.(2021全国乙理,4,5分)设函数f(x)=,则下列函数中为奇函数的是 (　　)A.f(x-1)-1　　　　B.f(x-1)+1　　　　C.f(x+1)-1　　　　D.f(x+1)+1答案　B　解题指导:思路一:将函数f(x)的解析式分离常数,通过图象变换可得函数图象关于(0,0)对称,此函数即为奇函数;思路二:由函数f(x)的解析式,求出选项中的函数解析式,由函数奇偶性定义来判断.解析　解法一:f(x)=-1+,其图象的对称中心为(-1,-1),将y=f(x)的图象沿x轴向右平移1个单位,再沿y轴向上平移1个单位可得函数f(x-1)+1的图象,关于(0,0)对称,所以函数f(x-1)+1是奇函数,故选B.解法二:选项A, f(x-1)-1=-2,此函数为非奇非偶函数;选项B, f(x-1)+1=,此函数为奇函数;选项C, f(x+1)-1=,此函数为非奇非偶函数;选项D, f(x+1)+1=,此函数为非奇非偶函数,故选B.5.(2021全国甲理,12,5分)设函数f(x)的定义域为R, f(x+1)为奇函数, f(x+2)为偶函数,当x∈[1,2]时, f(x)=ax2+b.若f(0)+f(3)=6,则f=              (　　)A.-答案　D　解题指导:利用奇偶性得到f(x+2)=-f(x),将出现的自变量0,3,对应的函数值转化为[1,2]内自变量对应的函数值,进而得到a,b以及f的值.解析　由题知从而f(x+4)=-f(x+2),即f(x+2)=-f(x),所以6=f(0)+f(3)=-f(2)+[-f(1)]=-(4a+b)-(a+b)=-5a-2b,即5a+2b=-6.①又由题知f(x+1)为奇函数,x∈R,所以f(1)=0,即a+b=0.②由①②得从而f(x)=-2x2+2,x∈[1,2].所以f.故选D.一题多解　因为f(x+1)与f(x+2)分别为奇函数和偶函数,所以函数f(x)的图象关于点(1,0)和直线x=2对称,且f(x)为周期函数,周期T=4,从而f(0)=-f(2),①f(3)=f(1)=0,②f,由①②结合f(0)+f(3)=6,知a=-2,b=2,所以f.6.(多选)(2022新高考Ⅰ,12,5分)已知函数f(x)及其导函数f '(x)的定义域均为R,记g(x)=f '(x).若f,g(2+x)均为偶函数,则              (　　)A. f(0)=0　　　　B.g=0C. f(-1)=f(4)　　　　D.g(-1)=g(2)答案　BC　解法一:若设f(x)=1,则g(x)=0,易知所设f(x)符合题意,此时f(0)=1,故选项A错误.设f(x)=sin(πx),则g(x)=f '(x)=πcos(πx),由于f=sinπ=sin=-cos(2πx),g(2+x)=πcos[π(2+x)]=πcos(2π+πx)=πcos(πx),所以f,g(2+x)均为偶函数,则所设f(x)符合题意.于是g(-1)=πcos(-π)=-π≠g(2),故选项D错误.由于f是偶函数,所以f '是奇函数,即g是奇函数,则g=0,注意到g(2+x)是偶函数,于是g=-g=g=0,故选项B正确.由f,取x=,则f(-1)=f(4),故选项C正确.故选BC.解法二:由题意知f⇔f(-x)=f(3+x)①,取x=1,知f(-1)=f(4),C正确.对①两边求导知-f '(-x)=f '(3+x)⇔f '(-x)=-f '(3+x),即g(-x)=-g(3+x)②,取x=-,知g=0.g(2+x)=g(2-x)⇔g(-x)=g(x+4)③,由②③知g(x+4)=-g(x+3),即g(x+1)=-g(x),所以g(x+2)=-g(x+1)=g(x).从而g=0,B正确.同解法一可判断A,D错误.故选BC. 7.(2017课标Ⅱ文,14,5分)已知函数f(x)是定义在R上的奇函数,当x∈(-∞,0)时, f(x)=2x3+x2,则f(2)=　　　　. 答案　12解析　本题主要考查运用函数的奇偶性求函数值.由题意可知f(2)=-f(-2),∵x∈(-∞,0)时, f(x)=2x3+x2,∴f(2)=-f(-2)=-[2×(-8)+4]=-(-12)=12.8.(2015课标Ⅰ理,13,5分)若函数f(x)=xln(x+)为偶函数,则a=　　　　. 答案　1解析　由已知得f(-x)=f(x),即-xln(-x)=xln(x+),则ln(x+)+ln(-x)=0,∴ln[()2-x2]=0,得ln a=0,∴a=1.9.(2014课标Ⅱ文,15,5分)偶函数y=f(x)的图象关于直线x=2对称, f(3)=3,则f(-1)=　　　　. 答案　3解析　∵函数y=f(x)的图象关于直线x=2对称,∴f(2+x)=f(2-x)对任意x恒成立,令x=1,得f(1)=f(3)=3,∴f(-1)=f(1)=3.10.(2012课标文,16,5分)设函数f(x)=的最大值为M,最小值为m,则M+m=　　　　. 答案　2解析　f(x)==1+,令g(x)=,则g(x)为奇函数,有g(x)max+g(x)min=0,故M+m=2.考点五 函数的周期性1.　(2016山东,9,5分)已知函数f(x)的定义域为R.当x<0时, f(x)=x3-1;当-1≤x≤1时, f(-x)=-f(x);当x>时, f=f.则f(6)=(　　)A.-2　　　B.-1　　　C.0　　　D.2答案　D　当x>时,由f=f可得f(x)=f(x+1),所以f(6)=f(1),而f(1)=-f(-1), f(-1)=(-1)3-1=-2,所以f(6)=f(1)=2,故选D.2.(2021全国甲文,12,5分)设f(x)是定义域为R的奇函数,且f(1+x)=f(-x).若f,则f= (　　)A.-答案　C　解题指导:求出函数f(x)的周期再进行转化,即可求解.解析　由f(1+x)=f(-x),且f(x)是定义在R上的奇函数,可得f(1+x)=f(-x)=-f(x),所以f(2+x)=-f(1+x)=f(x),所以f(x)的周期为2,则f,故选C.知识延伸:若函数f(x)为奇函数,且满足f(a+x)=f(-x),则f(x)图象的对称轴为直线x=,周期为2a;若函数f(x)为偶函数,且满足f(a+x)=f(-x),则f(x)图象的对称轴为直线x=,周期为a.3.(2022新高考Ⅱ,8,5分)已知函数f(x)的定义域为R,且f(x+y)+f(x-y)=f(x)f(y), f(1)=1,则f(k)= (　　)A.-3　　　　B.-2　　　　C.0　　　　D.1答案　A　令y=1,得f(x+1)+f(x-1)=f(x)①,故f(x+2)+f(x)=f(x+1)②.由①②得f(x+2)+f(x-1)=0,故f(x+2)=-f(x-1),所以f(x+3)=-f(x),所以f(x+6)=-f(x+3)=f(x),所以函数f(x)的周期为6.令x=1,y=0,得f(1)+f(1)=f(1)·f(0),故f(0)=2,同理,令x=1,y=1,得f(2)=-1;令x=2,y=1,得f(3)=-2;令x=3,y=1,得f(4)=-1;令x=4,y=1,得f(5)=1;令x=5,y=1,得f(6)=2.故f(1)+f(2)+f(3)+f(4)+f(5)+f(6)=0,所以f(k)=f(1)+f(2)+f(3)+f(4)=-3.故选A.4.(2022全国乙理,12,5分)已知函数f(x),g(x)的定义域均为R,且f(x)+g(2-x)=5,g(x)-f(x-4)=7.若y=g(x)的图象关于直线x=2对称,g(2)=4,则f(k)=              (　　)A.-21　　　　B.-22　　　　C.-23　　　　D.-24答案　D　由y=g(x)的图象关于直线x=2对称,得g(2+x)=g(2-x),故g(x)=g(4-x),由g(x)-f(x-4)=7,得g(2+x)-f(x-2)=7①,又f(x)+g(2-x)=5②,所以由②-①,得f(x)+f(x-2)=-2③,则f(x+2)+f(x)=-2④,所以由④-③,得f(x+2)=f(x-2),即f(x+4)=f(x),所以函数f(x)是以4为周期的周期函数.对于④,分别令x=1,2,得f(1)+f(3)=-2, f(2)+f(4)=-2,则f(1)+f(2)+f(3)+f(4)=-4.对于①,令x=-1,得g(1)-f(-3)=7,则g(1)-f(1)=7⑦,对于②,令x=1,得f(1)+g(1)=5⑧,由⑦⑧,得f(1)=-1.对于②,令x=0,得f(0)+g(2)=5,又g(2)=4,所以f(0)=1.对于③,令x=2,得f(2)+f(0)=-2,所以f(2)=-3.则=5×(-4)+f(1)+f(2)=-20+(-1)+(-3)=-24.故选D.5.(2021新高考Ⅰ,13,5分)已知函数f(x)=x3(a·2x-2-x)是偶函数,则a=　　　　. 答案　1解题指导:利用偶函数的定义,取定义域内的特殊值即可求出a的值.解析　∵f(x)=x3(a·2x-2-x)为偶函数,∴f(1)=f(-1),∴2a-,∴a=1.当a=1时, f(x)=x3(2x-2-x),定义域为R,且满足f(-x)=f(x),即f(x)为偶函数.一题多解　y=x3和y=2x-2-x为奇函数,利用结论:奇函数×奇函数=偶函数,可快速判断出a=1.6.(2022全国乙文,16,5分)若f(x)=ln+b是奇函数,则a=　　　　,b=　　　　. 答案　 -;ln 2解析　∵f(x)是奇函数,∴f(x)的定义域关于原点对称.由已知得x≠1,∴x≠-1,即当x=-1时,=0,∴a+=0,∴a=-,此时f(x)=ln+b,∵f(x)为奇函数且在x=0处有意义,∴f(0)=0,即ln+b=0,∴b=-ln=ln 2.综上可知,a=-,b=ln 2. 7.(2016四川,14,5分)已知函数f(x)是定义在R上的周期为2的奇函数,当0<x<1时, f(x)=4x,则f + f(1)=　　　　. 答案　-2解析　∵f(x)是定义在R上的奇函数,∴f(x)=-f(-x),又∵f(x)的周期为2,∴f(x+2)=f(x),∴f(x+2)=-f(-x),即f(x+2)+f(-x)=0,令x=-1,得f(1)+f(1)=0,∴f(1)=0.又∵f=f=-f=-=-2,∴f+f(1)=-2.