
















所属成套资源:2024年高考数学第一轮复习资料+讲解PPT
2024年高考数学第一轮复习10_专题四41导数的概念及运算(专题试卷+讲解PPT)
展开
这是一份2024年高考数学第一轮复习10_专题四41导数的概念及运算(专题试卷+讲解PPT),文件包含1_41导数的概念及运算分层集训pptx、1_41导数的概念及运算pptx、1_41导数的概念和运算十年高考docx、1_41导数的概念及运算docx等4份课件配套教学资源,其中PPT共43页, 欢迎下载使用。
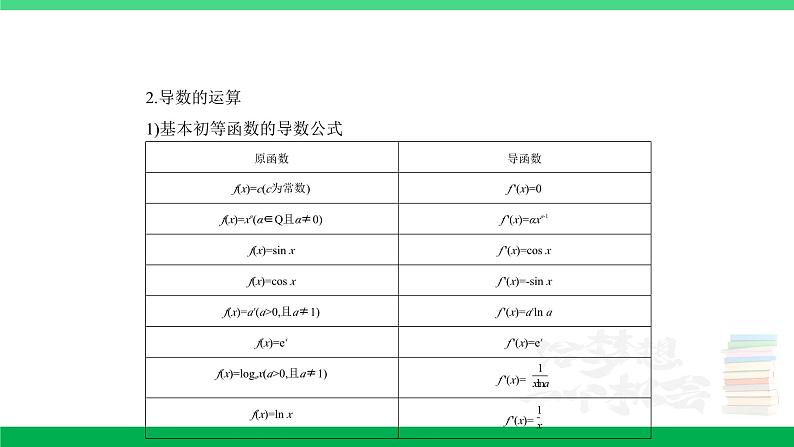
专题四 导数及其应用4.1 导数的概念及运算考点 导数的概念和运算1.(2016四川理,9,5分)设直线l1,l2分别是函数f(x)=图象上点P1,P2处的切线,l1与l2垂直相交于点P,且l1,l2分别与y轴相交于点A,B,则△PAB的面积的取值范围是( )A.(0,1) B.(0,2) C.(0,+∞) D.(1,+∞)答案 A 设l1是y=-ln x(0<x<1)的切线,切点P1(x1,y1),l2是y=ln x(x>1)的切线,切点P2(x2,y2),l1:y-y1=-(x-x1),①l2:y-y2=(x-x2),②①-②得xP=,易知A(0,y1+1),B(0,y2-1),∵l1⊥l2,∴-·=-1,∴x1x2=1,∴S△PAB=|AB|·|xP|=|y1-y2+2|·=·=·=·=·=,又∵0<x1<1,x2>1,x1x2=1,∴x1+x2>2=2,∴0<S△PAB<1.故选A.思路分析 设出点P1,P2的坐标,进而根据已知表示出l1,l2,然后求出点A、B的坐标及xP,最后利用点在曲线上及垂直的条件求出面积表达式,从而求出面积的取值范围.评析 本题考查了利用导数求切线问题,及考生的运算能力.2.(2014课标Ⅱ理,8,5分)设曲线y=ax-ln(x+1)在点(0,0)处的切线方程为y=2x,则a=( )A.0 B.1 C.2 D.3答案 D y'=a-,当x=0时,y'=a-1=2,∴a=3,故选D.3.(2021新高考Ⅰ,7,5分)若过点(a,b)可以作曲线y=ex的两条切线,则 ( )A.eb<a B.ea<b C.0<a<eb D.0<b<ea答案 D 解法一:当x→-∞时,曲线y=ex的切线的斜率k>0且k趋向于0,当x→+∞时,曲线y=ex的切线的斜率k>0且k趋向于+∞,结合图象可知,两切线的交点应该在x轴上方,且在曲线y=ex的下方,∴0<b<ea,故选D.解法二:易知曲线y=ex在点P(t,et)处的切线方程为y-et=et(x-t),∵切线过点(a,b),∴b-et=et(a-t),整理得et(t-a-1)+b=0.令f(t)=et(t-a-1)+b,则f '(t)=et(t-a),当t<a时, f '(t)<0,当t>a时, f '(t)>0,∴f(t)在(-∞,a)上单调递减,在(a,+∞)上单调递增,∴当t=a时, f(t)取得最小值f(a)=-ea+b.由已知得, f(t)的零点的个数即为过点(a,b)的切线条数,∴f(t)有且仅有2个零点.∴f(a)=-ea+b<0,即b<ea.①若b≤0,则当t<a时,t-a-1<0,et(t-a-1)<0,则f(t)<0,∴f(t)在(-∞,a)上无零点,而f(t)在[a,+∞)上至多有一个零点,不合题意.②若0<b<ea,由以上讨论可知,f(t)在(-∞,a)上为减函数,在(a,+∞)上为增函数,∴f(t)min=f(a)=-ea+b<0,且f(t)=b>0,f(a+1)=b>0,由零点存在性定理可知f(t)在(-∞,a)和[a,+∞)上各有一个零点,结合f(t)的单调性知f(t)有且只有两个零点.综上,0<b<ea.故选D.4.(2021全国甲理,13,5分)曲线y=在点(-1,-3)处的切线方程为 . 答案 y=5x+2解题指导:利用导数的几何意义求切线的斜率,利用点斜式得切线方程.解析 y=,所以y'=,所以k=y'|x=-1=5,从而切线方程为y+3=5(x+1),即y=5x+2.易错警示:①对分式型函数求导要注意公式的使用,先对分式进行化简可降低出错率.②要注意“在点处”和“过某点”的区别.5.(2022新高考Ⅱ,14,5分)曲线y=ln|x|过坐标原点的两条切线的方程为 , . 答案 y=x;y=-x(不分先后)解析 由题意可知,函数的定义域为{x|x≠0}.易证函数y=ln|x|为偶函数,当x>0时,y=ln x,设切点坐标为(x0,ln x0),∵y'=,∴切线斜率k=y',故切线方程为y-ln x0=(x-x0),又知切线过原点(0,0),∴-ln x0=-1,∴x0=e,故切线方程为y-1=(x-e),即y=x.由偶函数图象的对称性可知另一条切线方程为y=-x,故过坐标原点的两条切线方程为y=x和y=-x.6.(2022新高考Ⅰ,15,5分)若曲线y=(x+a)ex有两条过坐标原点的切线,则a的取值范围是 . 答案 (-∞,-4)∪(0,+∞)解析 设f(x)=(x+a)ex,则f '(x)=(x+a+1)ex,设切点为(x0,(x0+a)),因此切线方程为y-(x0+a)=(x0+a+1)(x-x0),又∵切线过原点(0,0),∴-(x0+a)=(x0+a+1)·(-x0),整理得+ax0-a=0,又切线有两条,∴关于x0的方程+ax0-a=0有两不等实根,故Δ=a2+4a>0,解得a>0或a<-4.7.(2019天津文,11,5分)曲线y=cos x-在点(0,1)处的切线方程为 . 答案 x+2y-2=0解析 本题通过求曲线在某点处的切线,考查学生对基本初等函数的导数公式、导数的运算法则、导数的几何意义的理解和掌握程度.∵y=cos x-,∴y'=-sin x-,∴y'|x=0=-,即曲线在(0,1)处的切线斜率为-,∴切线方程为y-1=-(x-0),即x+2y-2=0.方法总结 求曲线在某点处(注意:该点必为切点)切线的方法:①求导函数;②把该点横坐标代入,求出该点处导数值,即为切线的斜率;③用点斜式写出切线方程.8.(2018课标Ⅱ理,13,5分)曲线y=2ln(x+1)在点(0,0)处的切线方程为 . 答案 y=2x解析 本题主要考查导数的几何意义.因为y'=,所以y'|x=0=2,又(0,0)为切点,所以曲线在点(0,0)处的切线方程为y=2x.9.(2018课标Ⅱ文,13,5分)曲线y=2ln x在点(1,0)处的切线方程为 . 答案 2x-y-2=0解析 本题主要考查导数的几何性质.由y=2ln x得y'=.因为k=y'|x=1=2,点(1,0)为切点,所以切线方程为y=2(x-1),即2x-y-2=0.10.(2018课标Ⅲ理,14,5分)曲线y=(ax+1)ex在点(0,1)处的切线的斜率为-2,则a= . 答案 -3解析 本题考查导数的综合应用.设f(x)=(ax+1)ex,则f '(x)=(ax+a+1)ex,所以曲线在点(0,1)处的切线的斜率k=f '(0)=a+1=-2,解得a=-3.11.(2017课标Ⅰ文,14,5分)曲线y=x2+在点(1,2)处的切线方程为 . 答案 x-y+1=0解析 本题考查导数的几何意义.∵y=x2+,∴y'=2x-,∴y'|x=1=2-1=1,∴所求切线方程为y-2=x-1,即x-y+1=0.12.(2017天津文,10,5分)已知a∈R,设函数f(x)=ax-ln x的图象在点(1, f(1))处的切线为l,则l在y轴上的截距为 . 答案 1解析 本题主要考查导数的几何意义以及直线方程与截距.由题意可知f '(x)=a-,所以f '(1)=a-1,因为f(1)=a,所以切点坐标为(1,a),所以切线l的方程为y-a=(a-1)(x-1),即y=(a-1)x+1.令x=0,得y=1,即直线l在y轴上的截距为1.易错警示 不能正确求解函数的导数,而导致不能正确求解切线l的斜率.13.(2016课标Ⅱ理,16,5分)若直线y=kx+b是曲线y=ln x+2的切线,也是曲线y=ln(x+1)的切线,则b= . 答案 1-ln 2解析 直线y=kx+b与曲线y=ln x+2,y=ln(x+1)均相切,设切点分别为A(x1,y1),B(x2,y2),由y=ln x+2得y'=,由y=ln(x+1)得y'=,∴k==,∴x1=,x2=-1,∴y1=-ln k+2,y2=-ln k.即A,B,∵A、B在直线y=kx+b上,∴⇒评析 解决本题的关键是知道切点既在曲线上,又在切线上.14.(2015课标Ⅰ文,14,5分)已知函数f(x)=ax3+x+1的图象在点(1, f(1))处的切线过点(2,7),则a= . 答案 1解析 由题意可得f '(x)=3ax2+1,∴f '(1)=3a+1,又f(1)=a+2,∴f(x)=ax3+x+1的图象在点(1,f(1))处的切线方程为y-(a+2)=(3a+1)(x-1),又此切线过点(2,7),∴7-(a+2)=(3a+1)(2-1),解得a=1.15.(2015课标Ⅱ文,16,5分)已知曲线y=x+ln x在点(1,1)处的切线与曲线y=ax2+(a+2)x+1相切,则a= . 答案 8解析 令f(x)=x+ln x,求导得f '(x)=1+, f '(1)=2,又f(1)=1,所以曲线y=x+ln x在点(1,1)处的切线方程为y-1=2(x-1),即y=2x-1.设直线y=2x-1与曲线y=ax2+(a+2)x+1的切点为P(x0,y0),则y'=2ax0+a+2=2,得a(2x0+1)=0,∴a=0或x0=-,又a+(a+2)x0+1=2x0-1,即a+ax0+2=0,当a=0时,显然不满足此方程,∴x0=-,此时a=8.评析 本题主要考查导数的几何意义,能够利用点斜式求出切线方程是解题关键.16.(2015陕西理,15,5分)设曲线y=ex在点(0,1)处的切线与曲线y=(x>0)上点P处的切线垂直,则P的坐标为 . 答案 (1,1)解析 ∵函数y=ex的导函数为y'=ex,∴曲线y=ex在点(0,1)处的切线的斜率k1=e0=1.设P(x0,y0)(x0>0),∵函数y=的导函数为y'=-,∴曲线y=(x>0)在点P处的切线的斜率k2=-,则有k1k2=-1,即1·=-1,解得=1,又x0>0,∴x0=1.又∵点P在曲线y=(x>0)上,∴y0=1,故点P的坐标为(1,1).17.(2012课标文,13,5分)曲线y=x(3ln x+1)在点(1,1)处的切线方程为 . 答案 y=4x-3解析 y'=3ln x+1+x·=3ln x+4,k=y'|x=1=4,切线方程为y-1=4(x-1),即y=4x-3.评析 本题考查了导数的几何意义,考查了运算求解能力. 18.(2020新高考Ⅰ,21,12分)已知函数f(x)=aex-1-ln x+ln a.(1)当a=e时,求曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积;(2)若f(x)≥1,求a的取值范围.解析 f(x)的定义域为(0,+∞),f '(x)=aex-1-.(1)当a=e时,f(x)=ex-ln x+1,f '(1)=e-1,曲线y=f(x)在点(1,f(1))处的切线方程为y-(e+1)=(e-1)(x-1),即y=(e-1)x+2.直线y=(e-1)x+2在x轴,y轴上的截距分别为,2.因此所求三角形的面积为.(2)当0<a<1时,f(1)=a+ln a<1.当a=1时,f(x)=ex-1-ln x,f '(x)=ex-1-.当x∈(0,1)时,f '(x)<0;当x∈(1,+∞)时,f '(x)>0.所以当x=1时,f(x)取得最小值,最小值为f(1)=1,从而f(x)≥1.当a>1时,f(x)=aex-1-ln x+ln a≥ex-1-ln x≥1.综上,a的取值范围是[1,+∞).名师点评:本题第(2)问中,由不等式成立求参数的取值范围,常规解法是分离参数转化为求函数的最值问题,而本题中参数分布范围较广,无法分离,所以要对参数进行分类讨论,怎样分类是本题的一个难点,特别是当a>1时,证明f(x)≥1需要用到a=1时的结论,思路很窄,技巧性较强.19.(2022全国甲文,20,12分)已知函数f(x)=x3-x,g(x)=x2+a,曲线y=f(x)在点(x1, f(x1))处的切线也是曲线y=g(x)的切线.(1)若x1=-1,求a;(2)求a的取值范围.解析 解法一:由题意可知f '(x)=3x2-1, f(x1)=-x1,则曲线y=f(x)在点(x1, f(x1))处的切线方程为y-(-x1)=(3-1)(x-x1),即y=(3-1)x-2①.因为曲线y=f(x)在点(x1, f(x1))处的切线也是曲线y=g(x)的切线,所以有且仅有一组解,即方程x2-(3-1)x+2+a=0有两个相等的实数根,从而Δ=(3-1)2-4(2+a)=0⇔4a=9+1.(1)若x1=-1,则4a=12⇔a=3.(2)4a=9+1,令h(x)=9x4-8x3-6x2+1,则h'(x)=36x3-24x2-12x=12x(x-1)(3x+1),令h'(x)>0,得-<x<0或x>1,令h'(x)<0,得x<-或0<x<1,所以h(x)在和(1,+∞)上单调递增,在和(0,1)上单调递减,又h(1)=-4,h,所以h(x)≥-4,所以a≥-1.解法二:由题意可知f '(x)=3x2-1, f(x1)=-x1,则曲线y=f(x)在点(x1, f(x1))处的切线方程为y-(-x1)=(3-1)(x-x1),即y=(3-1)x-2①,设公切线与曲线y=g(x)的切点为(x2,+a),又g'(x2)=2x2,则切线可表示为y-(+a)=2x2(x-x2),即y=2x2x-+a②,因为①②表示同一直线方程,所以则(3-1)2-8+1.下面同解法一.易错警示:不能认为两曲线的公切线切点相同.20.(2022全国乙理,21,12分)已知函数f(x)=ln(1+x)+axe-x.(1)当a=1时,求曲线y=f(x)在点(0, f(0))处的切线方程;(2)若f(x)在区间(-1,0),(0,+∞)各恰有一个零点,求a的取值范围.解析 (1)当a=1时, f(x)=ln(1+x)+xe-x,其定义域为(-1,+∞),f '(x)=+(1-x)e-x,又f(0)=0,f '(0)=2,所以曲线y=f(x)在点(0,f(0))处的切线方程为y=2x.(2)f(x)=ln(1+x)+axe-x有零点,即方程ln(x+1)=-axe-x有根,设g(x)=ln(x+1),h(x)=-axe-x,因为f(x)在区间(-1,0),(0,+∞)各恰有一个零点,所以g(x)和h(x)的图象在(-1,0),(0,+∞)上各恰有一个交点.易知g'(x)=,h'(x)=-a(1-x)e-x,g(0)=h(0)=0.当x∈(-1,+∞)时,g'(x)>0,g(x)单调递增.①若a=0,显然不满足.②若a>0,则当x∈(-1,1)时,h'(x)<0,h(x)单调递减,当x∈(1,+∞)时,h'(x)>0,h(x)单调递增,此时g(x)和h(x)在(-1,0)上无交点.③若a<0,则当x∈(-1,1)时,h'(x)>0,h(x)在(-1,1)上单调递增,当x∈(1,+∞)时,h'(x)<0,h(x)在(1,+∞)上单调递减.(i)当x→+∞时,h(x)→0,g(x)→+∞,且g(0)=h(0)=0,要满足g(x)和h(x)的图象在(0,+∞)上有一个交点,需g'(0)<h'(0),解得a<-1;(ii)当x=-1时,h(-1)=ae,当x→-1时,g(x)→-∞,且g(0)=h(0)=0,要满足g(x)和h(x)的图象在(-1,0)上有一个交点,也需要g'(0)<h'(0),解得a<-1.综上所述,a的取值范围为(-∞,-1).
相关课件
这是一份2024年高考数学第一轮复习8_专题三34函数的图象(专题试卷+讲解PPT),文件包含1_34函数的图象分层集训pptx、1_34函数的图象pptx、1_34函数的图象十年高考docx、1_34函数的图象docx等4份课件配套教学资源,其中PPT共27页, 欢迎下载使用。
这是一份2024年高考数学第一轮复习5_专题三31函数及其性质(专题试卷+讲解PPT),文件包含1_31函数及其性质分层集训pptx、1_31函数及其性质pptx、1_31函数及其性质docx、1_31函数的概念及表示十年高考docx等4份课件配套教学资源,其中PPT共96页, 欢迎下载使用。
这是一份2024年高考数学第一轮复习41_专题资料包(专题试卷+讲解PPT),文件包含8_08-专题八立体几何docx、4_04-专题四导数及其应用docx、9_09-专题九平面解析几何docx、11_11-专题十一概率与统计docx、5_05-专题五三角函数与解三角形docx、7_07-专题七数列docx、3_03-专题三函数的概念与基本初等函数docx、2_02-专题二不等式docx、6_06-专题六平面向量docx、10_10-专题十计数原理docx、1_01-专题一集合与常用逻辑用语docx、12_12-专题十二数系的扩充与复数的引入docx等12份课件配套教学资源,其中PPT共0页, 欢迎下载使用。









