









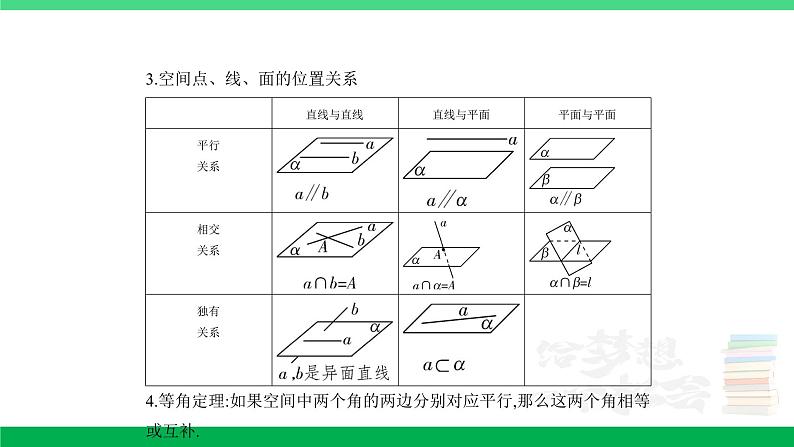


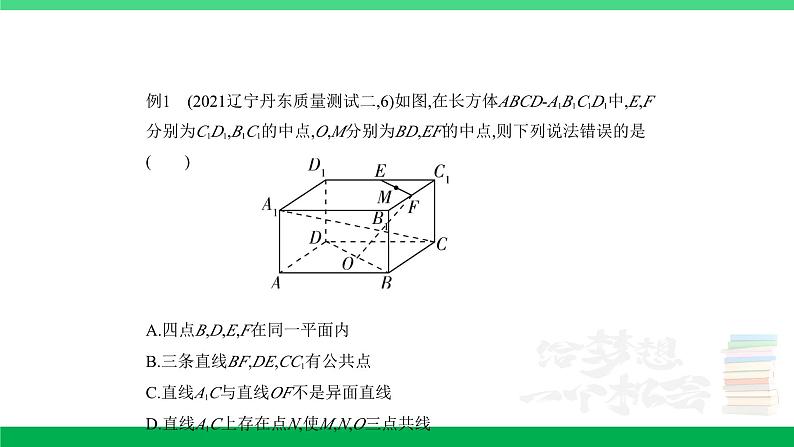
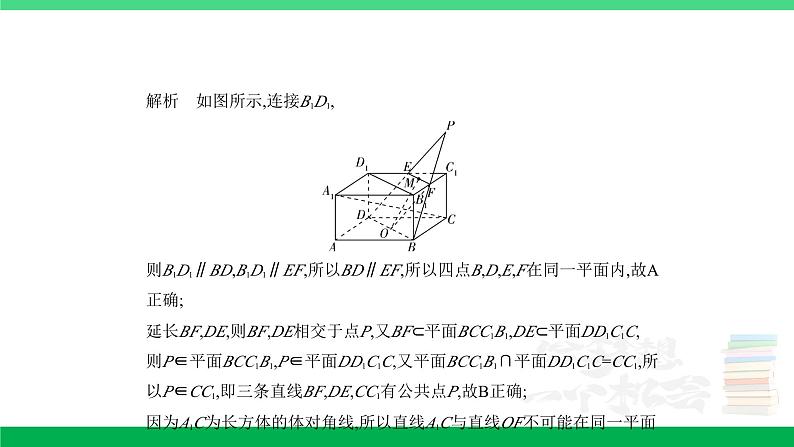







所属成套资源:2024年高考数学第一轮复习资料+讲解PPT
2024年高考数学第一轮复习23_专题八82点、线、面的位置关系(专题试卷+讲解PPT)
展开
这是一份2024年高考数学第一轮复习23_专题八82点、线、面的位置关系(专题试卷+讲解PPT),文件包含1_82点线面的位置关系分层集训pptx、1_82点线面的位置关系pptx、1_82空间点线面的位置关系十年高考docx、1_82点线面的位置关系docx等4份课件配套教学资源,其中PPT共45页, 欢迎下载使用。
8.2 空间点、线、面的位置关系考点一 点、线、面的位置关系1.(2015安徽理,5,5分)已知m,n是两条不同直线,α,β是两个不同平面,则下列命题正确的是( )A.若α,β垂直于同一平面,则α与β平行B.若m,n平行于同一平面,则m与n平行C.若α,β,则在α内与β平行的直线D.若m,n,则m与n垂直于同一平面答案 D 若α,β垂直于同一个平面γ,则α,β可以都过γ的同一条垂线,即α,β可以相交,故A错;若m,n平行于同一个平面,则m与n可能平行,也可能相交,还可能异面,故B错;若α,β不平行,则α,β相交,设α∩β=l,在α内存在直线a,使a∥l,则a∥β,故C错;从原命题的逆否命题进行判断,若m与n垂直于同一个平面,由线面垂直的性质定理知m∥n,故D正确.2.(2015浙江文,4,5分)设α,β是两个不同的平面,l,m是两条不同的直线,且l⊂α,m⊂β.( ) A.若l⊥β,则α⊥β B.若α⊥β,则l⊥mC.若l∥β,则α∥β D.若α∥β,则l∥m答案 A 对于选项A,由面面垂直的判定定理可知选项A正确;对于选项B,若α⊥β,l⊂α,m⊂β,则l与m可能平行,可能相交,也可能异面,所以选项B错误;对于选项C,当l平行于α与β的交线时,l∥β,但此时α与β相交,所以选项C错误;对于选项D,若α∥β,则l与m可能平行,也可能异面,所以选项D错误.故选A.3.(2015广东,6,5分)若直线l1和l2是异面直线,l1在平面α内,l2在平面β内,l是平面α与平面β的交线,则下列命题正确的是( )A.l与l1,l2都不相交B.l与l1,l2都相交C.l至多与l1,l2中的一条相交D.l至少与l1,l2中的一条相交答案 D 解法一:如图1,l1与l2是异面直线,l1与l平行,l2与l相交,故A,B不正确;如图2,l1与l2是异面直线,l1,l2都与l相交,故C不正确,选D.解法二:因为l分别与l1,l2共面,故l与l1,l2要么都不相交,要么至少与l1,l2中的一条相交.若l与l1,l2都不相交,则l∥l1,l∥l2,从而l1∥l2,与l1,l2是异面直线矛盾,故l至少与l1,l2中的一条相交,选D.4.(2014辽宁,4,5分)已知m,n表示两条不同直线,α表示平面.下列说法正确的是( ) A.若m∥α,n∥α,则m∥nB.若m⊥α,n⊂α,则m⊥nC.若m⊥α,m⊥n,则n∥αD.若m∥α,m⊥n,则n⊥α答案 B 若m∥α,n∥α,则m与n可能平行、相交或异面,故A错误;B正确;若m⊥α,m⊥n,则n∥α或n⊂α,故C错误;若m∥α,m⊥n,则n与α可能平行、相交或n⊂α,故D错误.因此选B.5.(2014广东理,7,5分)若空间中四条两两不同的直线l1,l2,l3,l4,满足l1⊥l2,l2⊥l3,l3⊥l4,则下列结论一定正确的是( )A.l1⊥l4B.l1∥l4C.l1与l4既不垂直也不平行D.l1与l4的位置关系不确定答案 D 由l1⊥l2,l2⊥l3可知l1与l3的位置不确定,若l1∥l3,则结合l3⊥l4,得l1⊥l4,所以排除选项B、C,若l1⊥l3,则结合l3⊥l4,知l1与l4可能不垂直,所以排除选项A.故选D.评析 本题考查了空间直线之间的位置关系,考查学生的空间想象能力、思维的严密性.6.(2014浙江文,6,5分)设m,n是两条不同的直线,α,β是两个不同的平面.( )A.若m⊥n,n∥α,则m⊥αB.若m∥β,β⊥α,则m⊥αC.若m⊥β,n⊥β,n⊥α,则m⊥αD.若m⊥n,n⊥β,β⊥α,则m⊥α答案 C 对于选项A、B、D,均能举出m∥α的反例;对于选项C,若m⊥β,n⊥β,则m∥n,又n⊥α,∴m⊥α,故选C.7.(2013课标Ⅱ理,4,5分)已知m,n为异面直线,m⊥平面α,n⊥平面β.直线l满足l⊥m,l⊥n,l⊄α,l⊄β,则( )A.α∥β且l∥αB.α⊥β且l⊥βC.α与β相交,且交线垂直于lD.α与β相交,且交线平行于l答案 D 若α∥β,则m∥n,这与m、n为异面直线矛盾,所以A不正确,α与β相交.将已知条件转化到正方体中,易知α与β不一定垂直,但α与β的交线一定平行于l,从而排除B、C.故选D.导师点睛 对于此类题,放入正方体中判断起来比较快捷.8.(2013广东理,6,5分)设m,n是两条不同的直线,α,β是两个不同的平面.下列命题中正确的是( )A.若α⊥β,m⊂α,n⊂β,则m⊥nB.若α∥β,m⊂α,n⊂β,则m∥nC.若m⊥n,m⊂α,n⊂β,则α⊥βD.若m⊥α,m∥n,n∥β,则α⊥β答案 D 若α⊥β,m⊂α,n⊂β,则m与n可能平行,故A错;若α∥β,m⊂α,n⊂β,则m与n可能平行,也可能异面,故B错;若m⊥n,m⊂α,n⊂β,则α与β可能相交,也可能平行,故C错;对于D项,由m⊥α,m∥n,得n⊥α,又知n∥β,故α⊥β,所以D项正确.9.(2011辽宁理,8,5分)如图,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不正确的是( )A.AC⊥SBB.AB∥平面SCDC.SA与平面SBD所成的角等于SC与平面SBD所成的角D.AB与SC所成的角等于DC与SA所成的角答案 D ∵四边形ABCD是正方形,∴AC⊥BD.又∵SD⊥底面ABCD,∴SD⊥AC.其中SD∩BD=D,∴AC⊥面SDB,从而AC⊥SB.故A正确.易知B正确.设AC与DB交于O点,连接SO.则SA与平面SBD所成的角为∠ASO,SC与平面SBD所成的角为∠CSO,又OA=OC,SA=SC,∴∠ASO=∠CSO.故C正确.由排除法可知选D.评析 本题主要考查了线面平行与垂直的判断及线面角、线线角的概念.属中档题.10.(2016浙江,2,5分)已知互相垂直的平面α,β交于直线l.若直线m,n满足m∥α,n⊥β,则( )A.m∥l B.m∥n C.n⊥l D.m⊥n答案 C ∵α∩β=l,∴l⊂β,∵n⊥β,∴n⊥l.故选C.11.(2020新高考Ⅰ,16,5分)已知直四棱柱ABCD-A1B1C1D1的棱长均为2,∠BAD=60°.以D1为球心,为半径的球面与侧面BCC1B1的交线长为 . 答案 解析 易知四边形A1B1C1D1为菱形,∠B1A1D1=60°,连接B1D1,则△B1C1D1为正三角形,取B1C1的中点O,连接D1O,易得D1O⊥B1C1,∴D1O⊥平面BCC1B1,取BB1的中点E,CC1的中点F,连接D1E,D1F,OE,OF,EF,易知D1E=D1F=,易知以D1为球心,为半径的球面与侧面BCC1B1的交线为以O为圆心,OE为半径的,∵B1E=B1O=1,∴OE=,同理OF=,易知EF=2,∴∠EOF=90°,∴的长=×(2π×)=.解题关键 利用题设条件证明D1O⊥平面BCC1B1,从而说明球面与侧面BCC1B1的交线是以O为圆心,OE为半径的是解题的关键. 12.(2016课标Ⅱ,14,5分)α,β是两个平面,m,n是两条直线,有下列四个命题:①如果m⊥n,m⊥α,n∥β,那么α⊥β.②如果m⊥α,n∥α,那么m⊥n.③如果α∥β,m⊂α,那么m∥β.④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.其中正确的命题有 .(填写所有正确命题的编号) 答案 ②③④解析 若m⊥n,m⊥α,n∥β,则α与β可能平行或相交,故①错误;②显然成立;若α∥β,m⊂α,则m与β无公共点,因而m∥β,故③正确;由线面角的定义、等角定理及面面平行的性质可知④正确.考点二 异面直线所成的角1.(2021全国乙理,5,5分)在正方体ABCD-A1B1C1D1中,P为B1D1的中点,则直线PB与AD1所成的角为 ( )A.答案 D 解题指导:利用平移法,连接BC1,则BC1∥AD1,得∠C1BP(或其补角)就是异面直线AD1与PB所成的角.解析 如图所示,连接BC1,C1P,易知四边形ABC1D1是平行四边形,∴BC1∥AD1,∴∠C1BP(或其补角)就是异面直线AD1与BP所成的角,设正方体的棱长为a,则BC1=a,C1P=a,连接AC、BD,设AC交BD于点O,连接OP,则OP⊥平面ABCD,∵OB⊂平面ABCD,∴OP⊥OB,∴PB=a.在△C1BP中,cos∠PBC1=,∴∠PBC1=,即直线PB与AD1所成的角为.故选D.方法总结:用几何法求异面直线所成角的具体步骤:2.(2016课标Ⅰ,理11,文11,5分)平面α过正方体ABCD-A1B1C1D1的顶点A,α∥平面CB1D1,α∩平面ABCD=m,α∩平面ABB1A1=n,则m,n所成角的正弦值为( )A. B. C. D.答案 A 如图,延长B1A1至A2,使A2A1=B1A1,延长D1A1至A3,使A3A1=D1A1,连接AA2,AA3,A2A3,A1B,A1D.易证AA2∥A1B∥D1C,AA3∥A1D∥B1C.∴平面AA2A3∥平面CB1D1,即平面AA2A3为平面α.于是m∥A2A3,直线AA2即为直线n.显然有AA2=AA3=A2A3,于是m,n所成的角为60°,其正弦值为.选A.3.(2014大纲全国理,11,5分)已知二面角α-l-β为60°,AB⊂α,AB⊥l,A为垂足,CD⊂β,C∈l,∠ACD=135°,则异面直线AB与CD所成角的余弦值为( )A. B. C. D.答案 B 在平面α内过点C作CE∥AB,则∠ECD为异面直线AB与CD所成的角(或其补角),不妨取CE=1,过点E作EO⊥β于点O.在平面β内过点O作OH⊥CD于点H,连接EH,则EH⊥CD.因为AB∥CE,AB⊥l,所以CE⊥l,又因为EO⊥β,所以CO⊥l.所以∠ECO为二面角α-l-β的平面角,即∠ECO=60°.因为∠ACD=135°,CD⊥l,所以∠OCH=45°.在Rt△ECO中,CO=CEcos∠ECO=1×cos 60°=.在Rt△COH中,CH=COcos∠OCH=cos 45°=.在Rt△ECH中,cos∠ECH===.所以异面直线AB与CD所成角的余弦值为.选B.4.(2014大纲全国文,4,5分)已知正四面体ABCD中,E是AB的中点,则异面直线CE与BD所成角的余弦值为( )A. B. C. D.答案 B 如图,取AD的中点F,连接EF、CF.因为E、F分别是AB、AD的中点,所以EF?BD,故∠CEF或其补角是异面直线CE、BD所成的角.设正四面体ABCD的棱长为a,易知CE=CF=a,EF=a.在△CEF中,由余弦定理可得cos∠CEF==.故选B.5.(2015浙江,13,5分)如图,在三棱锥A-BCD中,AB=AC=BD=CD=3,AD=BC=2,点M,N分别为AD,BC的中点,则异面直线AN,CM所成的角的余弦值是 . 答案 解析 连接DN,取DN的中点H,连接HM,由N、M、H均为中点,知|cos∠HMC|即为所求.因为AB=AC=BD=CD=3,AD=BC=2,又M,N为AD,BC的中点,所以CM⊥AD,AN⊥BC,所以CM==2,AN==2,MH=AN=,HC==,则cos∠HMC==.故异面直线AN,CM所成角的余弦值为.6.(2011北京文,17,14分)如图,在四面体PABC中,PC⊥AB,PA⊥BC,点D,E,F,G分别是棱AP,AC,BC,PB的中点.(1)求证:DE∥平面BCP;(2)求证:四边形DEFG为矩形;(3)是否存在点Q,到四面体PABC六条棱的中点的距离相等?说明理由.解析 (1)证明:因为D,E分别为AP,AC的中点,所以DE∥PC.又因为DE⊄平面BCP,PC⊂平面BCP,所以DE∥平面BCP.(2)证明:因为D,E,F,G分别为AP,AC,BC,PB的中点,所以DE∥PC∥FG,DG∥AB∥EF.所以四边形DEFG为平行四边形.又因为PC⊥AB,所以DE⊥DG.所以四边形DEFG为矩形.(3)存在点Q满足条件.理由如下:连接DF,EG,设Q为EG的中点.由(2)知,DF∩EG=Q,且QD=QE=QF=QG=EG.分别取PC,AB的中点M,N,连接ME,EN,NG,MG,MN.与(2)同理,可证四边形MENG为矩形,其对角线交点为EG的中点Q,且QM=QN=EG,所以Q为满足条件的点.
相关课件
这是一份2024年高考数学第一轮复习24_专题八83直线、平面平行的判定和性质(专题试卷+讲解PPT),文件包含1_83直线平面平行的判定和性质分层集训pptx、1_83直线平面平行的判定和性质pptx、1_83直线平面平行的判定和性质十年高考docx、1_83直线平面平行的判定和性质docx等4份课件配套教学资源,其中PPT共39页, 欢迎下载使用。
这是一份新高考数学二轮复习课件专题八 8.2 空间点、线、面的位置关系(含解析),共11页。PPT课件主要包含了答案④等内容,欢迎下载使用。
这是一份空间点、线、面的位置关系练习课件PPT,共28页。









